分类评估指标

Posted 2023-05-02

参考技术A # 准确率（Accuracy，ACC）

最常用、最经典的评估指标之一，计算公式为：

$ACC = \frac预测准确的样例数总预测数$

由此可见，准确率是类别无关的，衡量整个数据集的准确情况，即预测正确的样本所占的比例。

by the way，有时人们也会用错误率（Error Rate, ERR），与准确率定义相反，表示分类错误的样本所占的比例，计算公式为：

$ERR = 1 - ACC$

**存在问题**

在类别不平衡数据集中，ACC不能客观反映模型的能力。比如在三分类中，样本数量分布为（9800，100，100），那么模型只要无脑将所有样例都预测为A类即可以有98%的准确率，然而事实是模型根本没有分辨ABC的能力。因此下面引入精确率和召回率的概念。

# 概念定义

介绍精确率和召回率之前，我们先来了解几个概念：

| 名称 | 定义 |

| ------ | ------ |

| TP（True Positives，真阳性样本数）   | 被正确预测为正类别的样本个数 |

| FP（False Positives，假阳性样本数）  | 被错误预测为正类别的样本个数 |

| FN（False Negatives，假阴性样本数）   | 被错误预测为负类别的样本个数 |

| TN（True Negatives，真阴性样本数）   | 被正常预测为负类别的样本个数 |

注意：

* 第一个字母代表预测是否正确，第二个字母代表预测结果。Ground Truth（标签，数据的类别的真实情况，GT）则需要通过玩家组合这两个字母进行推理：预测正确则代表GT和预测结果一致，即TP的样本是正类别，TN的样本是负类别；反之FP的样本是负类别，FN的样本是正类别。搞清楚这个对精确率和召回率的了解会更加容易。

* 对于二分类而言，只要规定了正类别和负类别，这4个值是唯一的（负类别的TP等于正类别的TN，负类别的FP等于正类别的FN，负类别的FN等于正类别的FP，负类别的TN等于正类别的TP，因此对于二分类问题衡量正类别的指标就够了，因为两个类别是对等的）。对于多分类而言，用**One VS Others**的思想，将其中一类看作正类别，其他类看作负类别，**则每个类别都有这4个值，即这4个值在多分类中是与类别强相关的，每个类别的这几个值都不一样。**

# 混淆矩阵

混淆矩阵是所有分类算法模型评估的基础，它展示了模型预测结果和GT的对应关系。

| 推理类别/真实类别 | A | B | C | D |

| :----: | :----: | :----: | :----: | :----: |

| A | 56 | 5 | 11 | 0 |

| B | 5 | 83 | 0 | 26 |

| C | 9 | 0 | 28 | 2 |

| D | 1 | 3 | 6 | 47 |

其中矩阵所有元素之和为样本总数，每一行代表**预测为某类别的样本在真实类别中的分布**，每一列代表**某真实类别的样本在预测类别中的分布**。以A类为例，第一行代表预测为A的有72个样本（即TP+FP，56+5+11+0），第一列表示真实类别为A的有71个样本（即TP+FN，56+5+9+1）。其中TP为56，FP为16（行，5+11+0），FN为15（列，5+9+1），TN为195（即除第一行和第一列外所有的值之和）。样本总数等于混淆矩阵所有元素之和，即282。

如果用符号E来表示$B \cup C \cup D$，那么对于A来说，混淆矩阵可以改写如下：

| 推理类别/真实类别 | A | E |

| :----: | :----: | :----: |

| A | 56 | 16 |

| E | 15 | 195 |

由此可见，对于二分类来说，混淆矩阵的值与TP等指标对应如下：

| 推理类别/真实类别 | Positives（正类别） | Negatives（负类别） |

| :----: | :----: | :----: |

| Positives（正类别） | TP | FP |

| Negatives（负类别） | FN | TN |

对应多分类，可以用不同颜色来对应TP等指标的区域，使可视化效果更好，更方便理解。后续再更新。

# 精确率（Precision，$P$）

**对于某一类别而言**，预测为该类别样本中确实为该类别样本的比例，计算公式为：

$ P = \fracTPTP+FP$

以A、E的混淆矩阵为例：$ P_A = \frac5656+16=0.78, P_E = \frac19515+195=0.93$

以ABCD的混淆矩阵为例：$ P_A = 0.78, P_B = \frac835+83+0+26 = 0.73， P_C = \frac289+0+28+2=0.72, P_D = \frac471+3+6+47 = 0.83$

可以观察到，精确率的分母是混淆矩阵的行和，分子在对角线上。

# 召回率（Recall，$R$）

**对于某一类别而言**，在某类别所有的真实样本中，被预测（找出来，召回）为该类别的样本数量的比例，计算公式为：

$ R = \fracTPTP+FN$

以A、E的混淆矩阵为例：$ R_A = \frac5656+15 = 0.79, R_E = \frac19516+195 = 0.92$

以ABCD的混淆矩阵为例：$ R_A = 0.79, R_B = \frac835+83+0+3 = 0.91, R_C = \frac2811+0+28+6 = 0.62, R_D = \frac470+26+2+47 = 0.63$

可以观察到，召回率的分母是混淆矩阵的列和，分子在对角线上。

# F1

刚才提到，用ACC衡量模型的能力并不准确，因此要同时衡量精确率和召回率，遗憾的是，**一个模型的精确率和召回率往往是此消彼长的**。用西瓜书上的解释就是：挑西瓜的时候，如果希望将好瓜尽可能多地选出来（提高召回率），则可以通过增加选瓜的数量来实现（），如果将所有西瓜都选上（），那么所有的好瓜也必然被选上了，但是这样的策略明显精确率较低；若希望选出的瓜中好瓜比例可能高，则可只挑选最有把握的瓜，但这样就难免会漏掉不少好瓜，使得召回率较低。通常只有在一些简单任务中，才可能使得召回率和精确率都很高。因此我们引入F1来评价精确率和召回率的综合效果，F1是这两个值的调和平均（harmonic mean，与算数平均$\fracP+R2$和几何平均$\sqrtP*R$相比，调和平均更重视较小值），定义如下：

$ \frac1F1 = \frac12*(\frac1P+\frac1R)$

化简得：

$ F1 = \frac2*P*RP+R$

在一些应用中，对精确率和召回率的重视程度有所不同。例如在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容的确是用户感兴趣的，此时精确率更重要；而在逃犯信息检索系统中，更希望尽可能少漏掉逃犯，此时召回率更重要。$F1$的一般形式————$F_\beta$，能让我们表达出对精确率和召回率的不同偏好，它定义为：

$F_\beta = \frac(1+\beta^2)*P*R(\beta^2*P)+R$

其中$\beta > 0$度量了召回率对精确率的相对重要性。$\beta=1$时退化为标准$F1$；$\beta>1$时召回率有更大影响；$\beta<1$时精确率有更大影响。

以AE的混淆矩阵为例：

$F1_A = \frac2 * P_A * R_AP_A + R_A = \frac2 * 0.78 * 0.930.78+0.93 = 0.85$

$F1_E = \frac2 * P_E * R_EP_E + R_E = \frac2 * 0.93 * 0.920.93+0.92 = 0.92$

以ABCD的混淆矩阵为例：

$ F1_A = 0.85 $

$ F1_B = \frac2 * P_B * R_BP_B + R_B = \frac2 * 0.73 * 0.910.73+0.91 = 0.81$

$ F1_C = \frac2 * P_C * R_CP_C + R_C = \frac2 * 0.72 * 0.620.72+0.62 = 0.67$

$ F1_D = \frac2 * P_D * R_DP_D + R_D = \frac2 * 0.83 * 0.630.83+0.63 = 0.72$

# 多分类

以上指标除了准确率，其他指标都是类别相关的。要对模型做出总体评价，就需要算出所有类别综合之后的总体指标。求总体指标的方法有两种：宏平均（Macro Average）和微平均（Micro Average）。

**宏平均**

计算各个类对应的指标的算术平均

例，$F1_macro = \fracF1_A+F1_B+F1_C+F1_D4 = \frac0.85+0.81+0.67+0.724 = 0.7625$

所谓宏，就是从更宏观的角度去平均，即粒度是在类以上的。

**微平均**

先平均每个类别的TP、FP、TN、FN，再计算他们的衍生指标

例，

$TP_micro = \fracTP_A+TP_B+TP_C+TP_D4 = \frac56+83+28+474 = 53.5$

$FP_micro = \fracFP_A+FP_B+FP_C+FP_D4 = \frac16+31+11+104 = 17$

$FN_micro = \fracFN_A+FN_B+FN_C+FN_D4 = \frac15+8+17+284 = 17$

$TN_micro = \fracTN_A+TN_B+TN_C+FN_D4 = \frac195+160+226+1974=194.5$

$P_micro = \fracTP_microTP_micro+FP_micro = \frac53.553.5+17 = 0.7589$

$R_micro = \fracTP_microTP_micro+FN_micro = \frac53.553.5+17 = 0.7589$

$F1_micro = \frac2 * P_micro* R_microP_micro + R_micro = \frac2 * 0.7589 *0.75890.7589+0.7589 = 0.7589$

# 参考资料

1. 《西瓜书》

2. 《ModelArts人工智能应用开发指南》

如有错误，欢迎指出。下一期继续探讨ROC曲线、AUC曲线和PR曲线

分类模型评估指标汇总

作者：努力的孔子

https://www.cnblogs.com/yanshw/p/10735079.html

对模型进行评估时，可以选择很多种指标，但不同的指标可能得到不同的结果，如何选择合适的指标，需要取决于任务需求。

正确率与错误率

正确率：正确分类的样本数/总样本数，accuracy

错误率：错误分类的样本数/总样本数，error

正确率+错误率=1

这两种指标最简单，也最常用

缺点

1. 不一定能反应模型的泛化能力，如类别不均衡问题。

2. 不能满足所有任务需求

如有一车西瓜，任务一：挑出的好瓜中有多少实际是好瓜，任务二： 所有的好瓜有多少被挑出来了，显然正确率和错误率不能解决这个问题。

查准率与查全率

先认识几个概念

正样本/正元组：目标元组，感兴趣的元组

负样本/负元组：其他元组

对于二分类问题，模型的预测结果可以划分为：真正例 TP、假正例 FP、真负例 TN、 假负例 FN,

真正例就是实际为正、预测为正，其他同理

显然 TP+FP+TN+FN=总样本数

混淆矩阵

把上面四种划分用混淆矩阵来表示

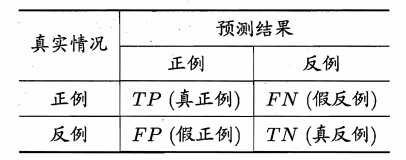
从而得出如下概念

查准率：预测为正里多少实际为正，precision，也叫精度

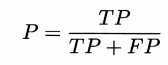
查全率：实际为正里多少预测为正，recall，也叫召回率

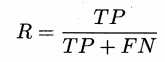
查准率和查全率是一对矛盾的度量。通常来讲，查准率高，查全率就低，反之亦然。

例如还是一车西瓜，我希望将所有好瓜尽可能选出来，如果我把所有瓜都选了，那自然所有好瓜都被选了，这就需要所有的瓜被识别为好瓜，此时查准率较低，而召回率是100%，

如果我希望选出的瓜都是好瓜，那就要慎重了，宁可不选，不能错选，这就需要预测为正就必须是真正例，此时查准率是100%，查全率可能较低。

注意我说的是可能较低，通常如果样本很好分，比如正的全分到正的，负的全分到负的，那查准率、查全率都是100%，不矛盾。

P-R曲线

既然矛盾，那两者之间的关系应该如下图

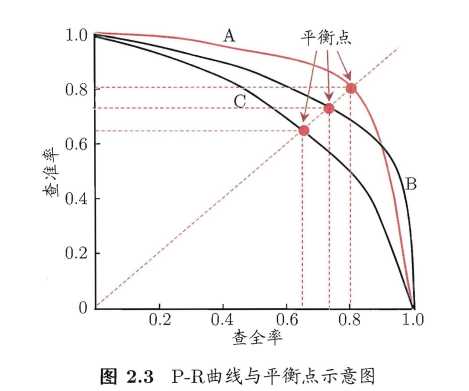
这条曲线叫 P-R曲线，即查准率-查全率曲线。

这条曲线怎么画出来的呢？可以这么理解，假如我用某种方法得到样本是正例的概率（如用模型对所有样本进行预测），然后把样本按概率排序，从高到低

如果模型把第一个预测为正，其余预测为负，此时查准率为1，查全率接近于0，

如果模型把前2个预测为正，其余预测为负，此时查准率稍微降低，查全率稍微增加，

依次...

如果模型把除最后一个外的样本预测为正，最后一个预测为负，那么查准率很低，查全率很高。

此时我把数据顺序打乱，画出来的图依然一样，即上图。

既然查准率和查全率互相矛盾，那用哪个作为评价指标呢？或者说同时用两个指标怎么评价模型呢？

两种情形

1. 如果学习器A的P-R曲线能完全“包住”学习器C的P-R曲线，则A的性能优于C

2. 如果学习器A的P-R曲线与学习器B的P-R曲线相交，则难以判断孰优孰劣，此时通常的作法是，固定查准率，比较查全率，或者固定查全率，比较查准率。

通常情况下曲线会相交，但是人们仍希望把两个学习器比出个高低，一个合理的方式是比较两条P-R曲线下的面积。

但是这个面积不好计算，于是人们又设计了一些其他综合考虑查准率查全率的方式，来替代面积计算。

平衡点：Break-Event Point，简称BEP，就是选择 查准率=查全率 的点，即上图，y=x直线与P-R曲线的交点

这种方法比较暴力

F1 与 Fβ 度量

更常用的方法是F1度量

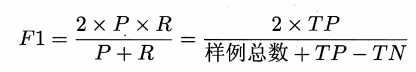
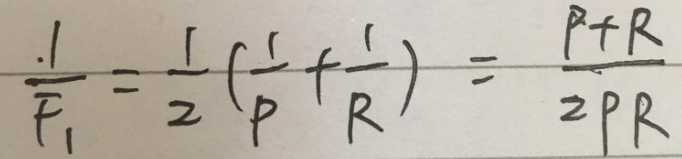
即 F1 是 P 和 R 的调和平均数。

与算数平均数 和 几何平均数相比，调和平均数更重视较小值。

在一些应用中，对查准率和查全率的重视程度有所不同。

例如商品推荐系统，为了避免骚扰客户，希望推荐的内容都是客户感兴趣的，此时查准率比较重要，

又如资料查询系统，为了不漏掉有用信息，希望把所有资料都取到，此时查全率比较重要。

此时需要对查准率和查全率进行加权

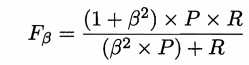
即 P 和 R 的加权调和平均数。

β>0，β度量了查全率对查准率的重要性，β=1时即为F1

β>1，查全率更重要，β<1，查准率更重要

多分类的F1

多分类没有正例负例之说，那么可以转化为多个二分类，即多个混淆矩阵，在这多个混淆矩阵上综合考虑查准率和查全率，即多分类的F1

方法1

直接在每个混淆矩阵上计算出查准率和查全率，再求平均，这样得到“宏查准率”，“宏查全率”和“宏F1”

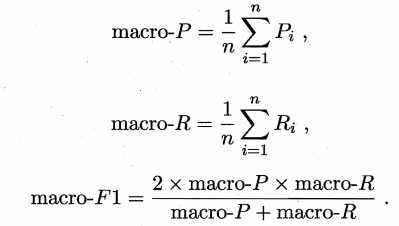
方法2

把混淆矩阵中对应元素相加求平均，即 TP 的平均，TN 的平均，等，再计算查准率、查全率、F1，这样得到“微查准率”，“微查全率”和“微F1”

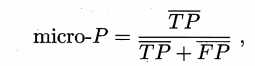
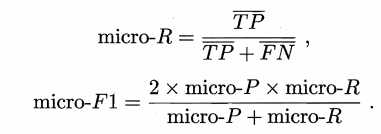
ROC 与 AUC

很多学习器是为样本生成一个概率，然后和设定阈值进行比较，大于阈值为正例，小于为负例，如逻辑回归。

而模型的优劣取决于两点：

1. 这个概率的计算准确与否

2. 阈值的设定

我们把计算出的概率按从大到小排序，然后在某个点划分开，这个点就是阈值，可以根据实际任务需求来确定这个阈值，比如更重视查准率，则阈值设大点，若更重视查全率，则阈值设小点，

这里体现了同一模型的优化，

不同的模型计算出的概率是不一样的，也就是说样本按概率排序时顺序不同，那切分时自然可能分到不同的类，

这里体现了不同模型之间的差异，

所以ROC可以用来模型优化和模型选择，理论上讲 P-R曲线也可以。

ROC曲线的绘制方法与P-R曲线类似，不再赘述，结果如下图

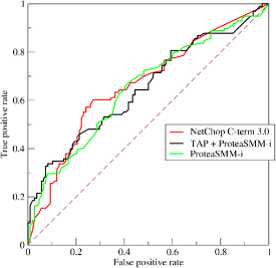
横坐标为假正例率，纵坐标为真正例率，曲线下的面积叫 AUC

如何评价模型呢？

1. 若学习器A的ROC曲线能包住学习器B的ROC曲线，则A优于B

2. 若学习器A的ROC曲线与学习器B的ROC曲线相交，则难以比较孰优孰劣，此时可以比较AUC的大小

总结

1. 模型评估主要考虑两种场景：类别均衡，类别不均衡

2. 模型评估必须考虑实际任务需求

3. P-R 曲线和 ROC曲线可以用于模型选择

4. ROC曲线可以用于模型优化

参考资料：

周志华《机器学习》

本文由博客一文多发平台 OpenWrite 发布！