无标度网络模型开山之作：随机网络中标度的涌现

Posted 2021-04-07 集智俱乐部

导语

度分布满足幂律分布的网络即为无标度网络，互联网、基因网络、社会网络等网络都具有无标度性或满足幂律分布。1999 年 10 月 15 日的Science 杂志，刊登了 Albert-László Barabási 和 Réka Albert 的文章，提出通过网络生长和偏好依附的模型，可以获得无标度网络，后被称为 B-A 模型。这一模型的提出，是网络科学里程碑式的工作。这项研究之后，关于复杂网络的研究如雨后春笋，层出不穷。B-A 网络模型与1998 年 Duncan Watts 等提出的小世界网络模型，共同宣告网络科学领域的正式形成。

论文题目：

Emergence of scaling in random networks

https://science.sciencemag.org/content/286/5439/509

无标度网络现象

无标度一词来源于幂律分布的标度不变性，指的是幂指数函数 的自变量 x 经过某个常数放大或缩小c倍后，其函数关系仍然为幂指数函数。即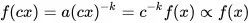：       ，下图可以更直观的看到这一现象，其中左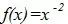图为 ，右图为。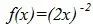

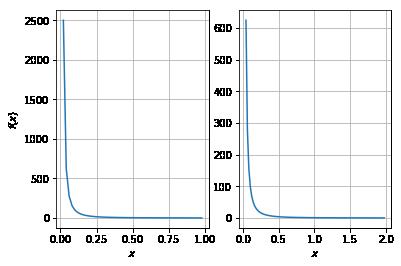
图1：幂律分布标度不变，a=1，k=2，c=0.5

相应的，无标度网络指的是度分布（近似）为幂律分布的网络模型。用度分布 P(k)  表示网络中有 k 条连边的节点出现的频数, 其分布 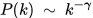 ，其中幂指数λ是描述网络的一个参数。换句话来说，无标度网络中大多数节点只与少数节点连接，而少量的节点拥有极其多的节点连接，这种少量节点称为枢纽或集散节点（hub）。

相关阅读：

https://wiki.swarma.org/index.php?title=无标度网络_Scale-free_network

无标度网络（Scale-free network）这一概念正式出现于 1999 年发表的《随机网络中标度的涌现》一文中，作者是网络科学家巴拉巴西（Albert-László Barabási）和艾伯特（Réka Albert），因此也称为 B-A 模型。

相关阅读：

https://wiki.swarma.org/index.php?title=艾伯特-拉斯洛·巴拉巴西_Albert-László_Barabási

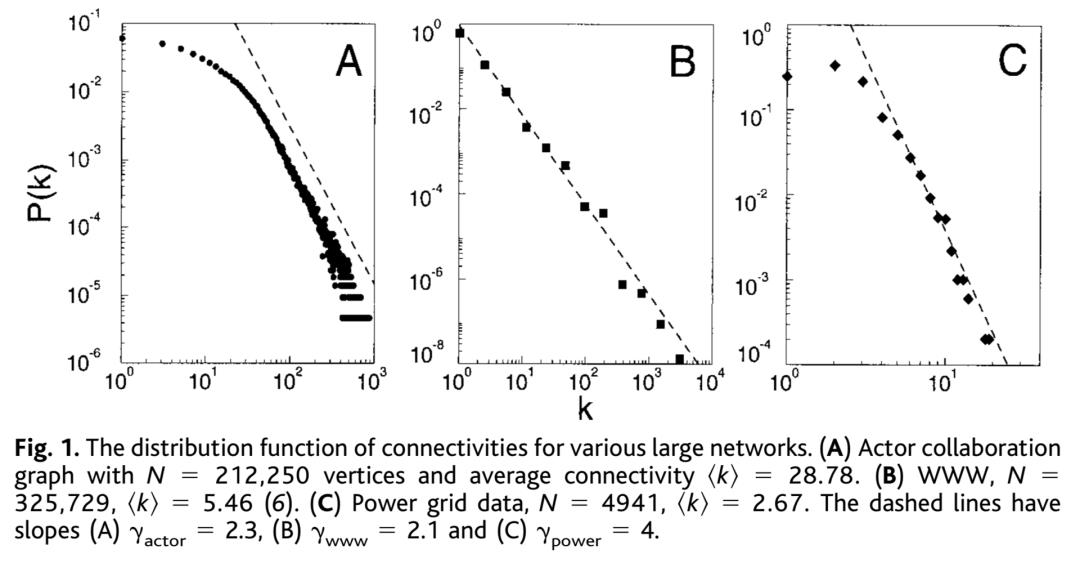
图2：A-明星合作网络；B-万维网；C-电力网络度分布

原文中，作者将 P(k)-k 关系图的坐标对数化来更直观的体现明星合作网络、万维网和电力网络一定程度上符合无标度网络模型，从中提炼模型，并提出这一模型在自然界大型网络中潜在的应用价值。

无标度网络的生成：

生长模型和偏好依附

原文中，作者介绍了一种简单而合理的无标度网络生成机制。首先，这个模型基于两个假设：1. 生长机制：网络会随着时间的推移不断产生新的节点；2. 优先连接：加入的新节点会倾向于与有更多连接的节点相连。打个比方，会不断的有新用户加入微博，而粉丝较多的名人被新用户关注的几率更高。

 

在这种假设下，BA 模型的具体构造为：

1. 增长：从一个较小的网络 G 0 开始（这个网络有  n 0 个节点，E 0条边），逐步加入新的节点，每次加入一个。
2. 连接：假设原来的网络已经有 n 个节点（ s 1， s 2，...， s n）。在某次新加入一个节点  s n+1 时，从这个新节点向原有的 n 个节点连出  m< n 0 个连结。
3. 优先连接：连接方式为优先考虑高度数的节点。对于某个原有节点  s i  （1≤i≤n），将其在原网络中的度数记作 d i ，那么新节点与之相连的概率 P i  为：        

这样，在经过 t 次之后，得到的新网络有  n 0 +t 个节点，一共有 E 0 +mt 条边。

 

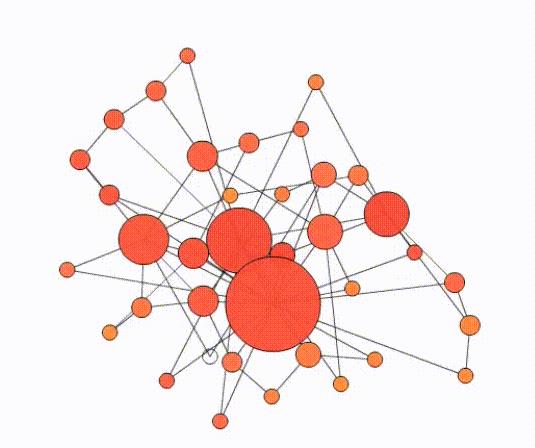
图3：增长和偏好依附

 

作者通过控制变量法，证明了生长和优先连接两条假设是产生无标度分布的必要条件。

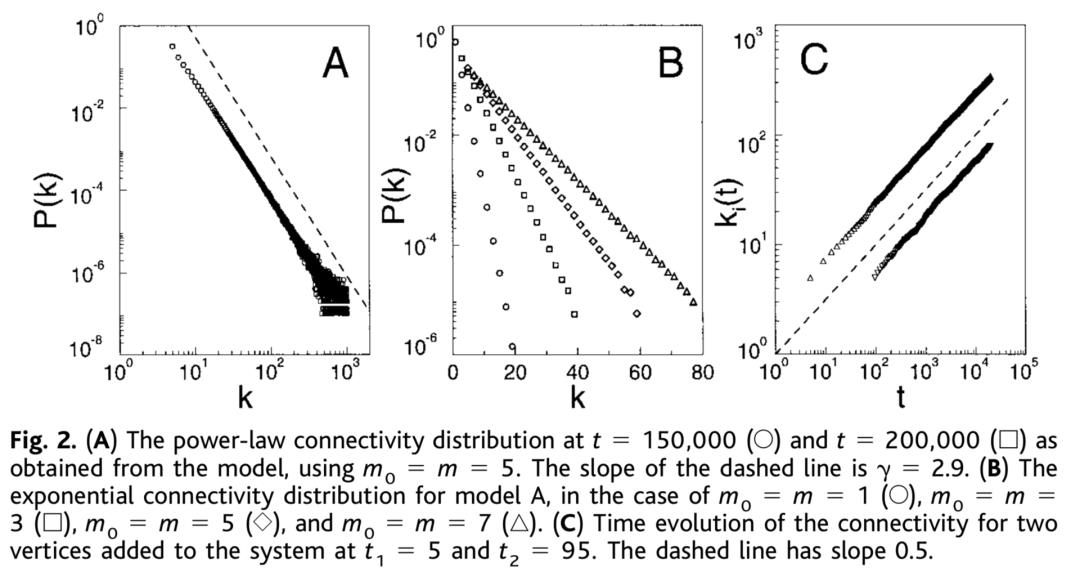
图4：生长机制和优先连接产生标度不变性

A 图表示的是起始有 5 个节点，每个时间间隔加入的节点将与其他 5 个节点产生连接，时间为 150000（◯）和 200000（▢）时网络的度分布情况，◯和▢分布基本呈以指数为虚线的斜率的幂律分布，说明无标度网络中度分布与时间无关。

 

B 图模拟的是保留生长机制，用等概率产生新连接代替优先连接的网络模型，图例◯、▢、◇、▷对应的是起始节点和节点产生新连接数均为 1、3、5、7 四种不同的对比情况。注意，此时表示连接度k的坐标轴没有对数化处理，即 P(k)~exp(-βk)，此时无标度现象消失了！

若网络中节点不增加，一直保持 N 个节点，节点之间不断进行优先连接，经历约 N^2 时间间隔后，所有节点互相连接，节点的度分布也不符合幂律分布。

通过控制变量法分别对两个假设进行检验，生长和优先连接对于无标度网络的产生来说缺一不可。

 

C 图说明的是在优先连接的假设下，两个节点起始时连接度的差别会随着时间增大，即人们熟知的“富人更富”这一现象。ki(t) 是 t 时刻节点i的连接度。t=5 和 t=95 时在初始网络中加入一个节点，先加入的节点记为节点 1，后加入记为节点 2 。因为优先连接，节点1的连接度一直高于节点 2，并且这两点之间连接度之差随着时间增大而越来越大！

无标度网络的性质及应用

首先是 鲁棒且脆弱性。 鲁棒性指的是抵抗干扰的能力强，脆弱性说明抵御干扰能力差。无标度网络是如何同时存在这两种“矛盾”的性质于一体呢？作者通过对无标度网络进行不同类型的攻击来解释这一性质。

图5：移除的节点比例与特征路径长度示意图

图5横轴为移除的节点比例，随机失效（Failure）指随机移除节点，刻意攻击（Attack）指从度最大的节点开始移除。纵轴 d 表示任意两个节点之间最短距离的平均长度 ，即特征路径长度，描述网络的全局特征 。

通过图5中随机网络和无标度网络中随机失效和刻意攻击不同情形相互对比，无标度网络在随机失效情形下，其全局特征无明显变化；而在刻意攻击情形下，全局性质变化十分明显。相比之下，随机网络在两种节点移除情形下，全局变化趋势一致，且变化较缓。这说明无标度网络对于随机失效的鲁棒性和对于有目的攻击的脆弱性，即针对不同类型的攻击，无标度网络将产生不同程度的变化或反应。

 

这在社会舆论管理中有重要的应用。比如，微博上一些大V散播谣言就会被禁言，这相当于网络中重要的这些节点被移除，那么整个微博信息网络就会从谣言或者是从一些不良信息的传播里面恢复到正常。

 

此外，在无标度网络上研究病毒传播，会发现无标度网络上病毒不能被根除！

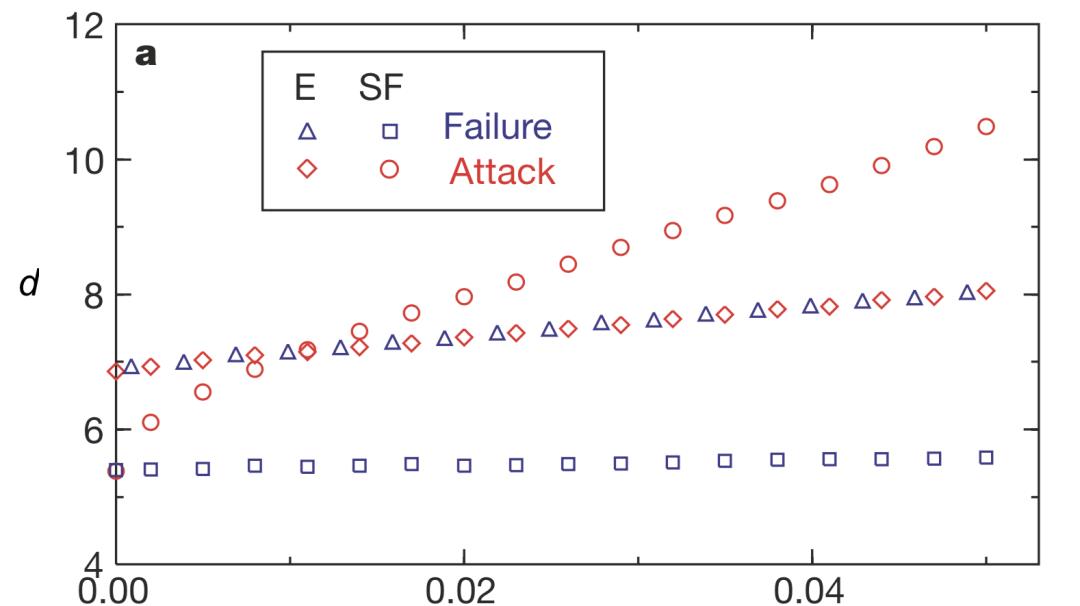
无标度网络的思想起源与热点讨论

人们很早就发现幂律分布规律广泛存在于现实中的网络中，比如 1897 年意大利经济学家帕累托提出“二八定律”，Lotka、Yule、Zipf 和 Simon 等人发现论文引用网络、生物网络等网络中节点的度分布都满足幂律分布。1976年，Price 归纳这些网络中节点的度分布规律，用数学模型推导这一现象的原因，并提出了累积优势这一说法解释“富人更富”这一现象。这些研究中已经有无标度网络模型的影子，Price 提出的模型及 BA 模型的无向形式。

 

《随机网络中的标度涌现》末尾，作者表示无标度网络模型可广泛应用于商务、社交、交通等现实网络的研究。由于无标度网络定义中没有给出严格的定义，“度分布为渐进为幂律分布” 只要求度分布尾服从幂指数衰减，因此在理解和判断无标度网络度分布问题上，网络科学共同体还未达成共识，不少学者对无标度网络是否广泛存在于现实存在质疑。确实，将横纵坐标对数化之后满足分布呈直线只是满足幂律分布的必要而不充分条件，此时的函数关系是否严格符合幂律分布也是统计学中研究的热点。

 

其中引起学术界较大争议的的质疑来自于 2018 年科罗拉多大学博尔德分校的学者，在论文《Scale-free networks are rare》中，他们设计了一种严格的统计方法测试网络是否服从无标度的特性，并对将近 1000 个网络进行了严格的统计性检验，得出现实世界中无标度网络不具有普遍性的结论。随后，Barabási 也对质疑做出了回应。

网络科学作为一门新兴交叉学科，其中的难题会吸引来自不同领域的学者，他们讨论问题时的角度也会有差别，尤其是讨论“是否存在普遍性”相关的难题。网络科学领域目前还没有普适的理论， 为了网络科学发展成熟，也许基础理论的研究还需要多下功夫。

论文题目：

Scale-free networks are rare

https://www.nature.com/articles/s41467-019-08746-5

相关阅读：

编辑：张爽

推荐阅读

---

商务合作及投稿转载｜[e-mail]

◆ ◆ ◆

加入“没有围墙的研究所”

让苹果砸得更猛烈些吧！