BNN领域开山之作——不得错过的训练二值化神经网络的方法

Posted 2022-03-30 奥比中光3D视觉开发者社区

作者‖ cocoon
编辑‖ 3D视觉开发者社区

文章目录

• 导读
• 概述
• 方法
• • 确定二值化以及随机二值化
  • 梯度计算以及累加
  • 离散化梯度传播
  • 乘法运算优化
  • • 基于位移（shift）的BN
    • 基于位移的AdaMax
  • 不做二值化的第一层
• 实验
• • 论文实验结果
  • nni中的调用
• 结语
• 参考文献

导读

相较于32位的浮点数神经模型，二值化神经网络通过将权值和隐藏层激活值二值化为1或者-1，达到更高的速度和更小的存储空间，从而使神经网络在移动设备上运行成为可能，其研究意义与价值不可言喻。而该篇论文作为BNN领域的开山之作，提供了一种训练二值化神经网络的方法，并通过实验证明该方法可达到接近SOTA的结果。代码开源，值得一读！

论文链接： https://arxiv.org/pdf/1602.02830.pdf

代码链接：https://github.com/itayhubara/BinaryNet

概述

该论文是2016年的“老”文章，源于Bengio大神等人，是BNN领域的经典文章。BNN相比起普通的32位的浮点数神经网络模型而言，内存占用理论上缩减至$\frac{1}{32}$，且由于参数二值的性质，可以将多数运算转变为按位运算，进而有着对移动端非常友好的优势。尽管BNN有着巨大的优势，其特性也带来了网络精度降低以及难以训练的问题。该论文则提供了一种训练BNN的方法，并通过实验证明该方法可以在MNIST，CIFAR-10以及SVHN上面获得接近SOTA的结果。NNI（Neural Network Inteligence）是著名的开源AutoML工具，其对该BNN论文已进行了复现，用户可方便地对其进行调用。

方法

确定二值化以及随机二值化

所谓的确定二值化，指使用一种固定的方式将实值转为二值（+1或-1），转换公式为：
$$x^b=\mathrm{Sign}(x)=\begin{array}{ll}+1& \text{ if }x\ge 0\\ -1& \text{ otherwise }\end{array}$$
而所谓的随机二值化的转换公式为：
$$x^b=\begin{array}{ll}+1& \text{ with probability }p=\sigma (x)\\ -1& \text{ with probability }1-p\end{array}$$
其中的$\sigma$指 “hard sigmoid” 函数，具体为：
$$\sigma (x)=\mathrm{clip}\left(\frac{x+1}{2},0,1\right)=\max \left(0,\min \left(1,\frac{x+1}{2}\right)\right)$$
尽管随机二值化看起来更吸引人，但是在具体实现的时候需要硬件产生随机位，因此，除了某些特定的实验以外，文章主要采用确定二值化的方式。

梯度计算以及累加

尽管BNN的训练方法使用的是二值的权重以及激活函数，但是参数的梯度的计算以及累加，是需要高精度的浮点数的。其实有存在很极端的二值网络连梯度也二值化，但是显然在该论文中是没有这么做的。

对于SGD这类的优化算法来说，浮点的梯度值很可能是必要的。SGD总是会用很小又带有噪声的步子去探索参数空间，而普遍认为这种噪声是服从正态分布的，因而可以在梯度的累加过程中消除掉噪声。也就是说，我们希望梯度的累加是足够细腻的，换句话说，高精度似乎是必须的。此外，这样的噪声可以被认为是某种正则化，进而会有助于泛化。本文中训练BNN的方式可以看做是“Dropout”的一个变种，只不过不是随机的对部分激活函数置为0，而是将所有的激活以及权重二值化。

离散化梯度传播

符号函数的导数几乎处处为0，这使得其难以进行常规的反向传播。因此，我们只能寻找一种方式对其进行“松弛”。Bengio（2013）等人的研究表明STE（straight-through estimator）有着快速训练的优势，STE实质上就是将二值参数的梯度直接作为对应的浮点数的梯度。

STE 过程简介：

假设我们现在有浮点型的模型，每次都在更新浮点权重的梯度。在前向推理时，我们对浮点型的模型进行了二值化，得到推理结果后再反向传播出二值参数的梯度，并使用这二值参数的梯度直接作为浮点数的梯度，用以更新浮点数的权重。训练结束后，直接对浮点型的参数做最后一次二值化，形成最终的二值网络。

因此，该论文也借鉴了STE的思想。考虑到符号函数的表达为：

$$q=Sign(r)$$
假设$g_q$为$q$的梯度，计算方式为$g_q=\frac{\partial C}{\partial q}$，其中$C$为损失函数，如果$g_q$已知，那么$\frac{\partial C}{\partial r}$的STE就可以简单地表达为：
$$g_r=g_q{1}_{|r|\le 1}$$
这样做将保持梯度的信息，解决掉符号函数导数都为0的问题。且这样做可以在实数$r$过大（具体指绝对值大于1的时候）时取消掉梯度，因为如果当$r$太大时不取消梯度的话，会对训练造成恶劣的影响，而对于实数$r$的绝对值在1以内的时候，实数$r$的梯度与$q$一致。$1_{|r|\le 1}$可以被认为是使用一种hard tanh的方式对梯度进行传播，相当于逐段的线性激活函数：
$$\mathrm{Htanh}(x)=\mathrm{Clip}(x,-1,1)=\max (-1,\min (1,x)).$$
hard tanh的图形表现为：

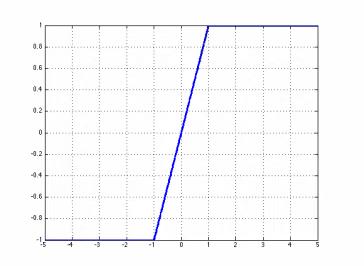
对于隐藏单元，我们使用非线性的符号函数来获得二值的激活函数，此外，对于权重的二值化，有以下的两个小点需要注意：

• 限制每一个实值的权重在$[-1,1]$的范围内，对于那些数值在$[-1,1]$范围以外的权重$w^r$，将其投影到1或者是-1的两个值上；
• 对于实数权重$w^r$，使用符号函数对其进行量化，即$w^b=Sign(w^r)$。

具体地，这样的STE的方法在前向传播时，有：

在反向传播时，则有：

值得注意的是，在伪代码中已经清晰表明梯度并非二值的，这在“2.2 梯度计算以及累加”中也进行了强调。其中，将二值化也看做一层，因此需要先求得二值化层的梯度，此外，网络所求得的梯度尽管是高精度的浮点数，但其作用的对象是二值后的权值，并非二值化前的浮点数。

关于参数梯度的累加，有：

乘法运算优化

基于位移（shift）的BN

BN层加速了训练速度并且减小了权重尺度的整体影响。这种归一化的噪声或许有助于模型的正则化，然而，在训练时，BN层需要许多的乘法运算，尽管说这种乘法运算的数量与网络中的神经元数量一致，但是对于许多网络来说，这个数量还是相当大的。举个例子，对于这篇文章中所使用的网络架构，第一层卷积包含了$128\ast 3\ast 3$的卷积掩膜，也就是说，它将一个大小为$3\ast 32\ast 32$的影像转换为$3\ast 128\ast 28\ast 28$，这个量级已经是权重量级的数倍了。为了得到BN层所能达到的效果，文章提出了一个所谓的$SBN$（shift-based batch normalization）的技巧。具体见以下算法描述：

SBN的好处在于几乎不需要乘法运算。此外，在实验中，发现使用SBN相对于BN而言，几乎没有精度损失。

基于位移的AdaMax

ADAM的优化方式似乎也减小了权重尺度的影响，由于ADAM也需要做许多的乘法运算，文章建议使用基于位移的AdaMax，具体见以下算法描述：

同样地，文章在实验中发现，使用基于位移的AdaMax相对于普通的Adam算法来说，也没有观察到精度损失。

不做二值化的第一层

在BNN中，某一层的输出将作为下一层的输入，而所有层的输入，我们会希望它们都是二值的。这里有一个例外，就是第一层，或者说是输入的图像特征的编码并非二值。然而，文章认为，输入的影像通道数相比起网络内部的高维来说是非常少的，即使是彩色影像，也只有RGB三个通道，且往往影像值都在$[0,255]$之间，所以可以用8比特来表示。其次，将连续数值的输入视作定点数相对来说是比较简单的，举例来说，常用的8位量化定点输入为：
$$\begin{array}{rl}& s=x\cdot w^b\\ & s=\sum _{n=1}^8{2}^{n-1}\left(x^n\cdot w^b\right)\end{array}$$
其中，假设$x$是一个长度为$1024$（ 32 ∗ 32 32 * 32 第61篇AlexNet：CNN开山之作

Two-Stream Convolutional Networks for action Recognition in Video 视频理解领域的开山之作

ViT：Transformer在CV领域的开山之作

GNN教程图神经网络“开山之作”！

代码实现MNLM | word embedding开山之作

大型园区网络排错篇之概念开山之作