数学意义上的四维正五面体在三维上展开有几种立体形状？

Posted 2023-04-30

如同三维的正四面体在二维展开，他有三种形状，如图（自己画的，不太好看）
问题任然有效

你说是在三维展开吗，
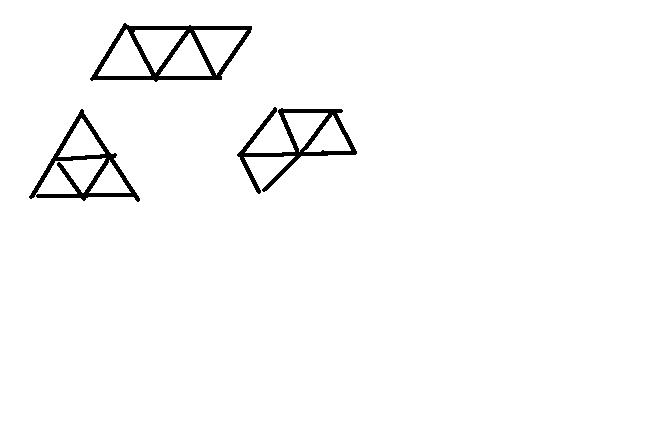
那个好说，就是5个正四面体，其中任何一个正四面体都和其他的4个正四面体共面。并且这个共同的面就是正四面体的一个面。

如果说三维展开的话，容易，准备五个正四面体，每个面任意拼接就行了。总共有三种拼接方法。

楼主学过化学吗，就像是戊烷的三种同分异构太一样。 参考技术A 四维通常来说是加上时间维。空间物体在不同时间的不同情况。
如果要描述四维空间的物体，就是把第四个变量不变，产生的三维图形。

对于正五面体，在四维到三维的展开是不变的。不要太异想天开。 参考技术B 我的理解是6种！追问

给个图呗~~~

追答

亲，二维里面你要我画个四维的？

追问

不是啊~~你说的6种三维图嘛~~

世界上有没有正五面体？

平面图形里有正三角形，三维空间里有正四面体（四个顶点，四个面，六条棱 ），那么进一步问，有没有正五面体？   实际上，三维空间中只存在五种正多面体，分别是正四面体、正六面体、正八面体、正十二面体、正二十面体。可以通过欧拉定理得出该结论。

欧拉定理如下：如果一个凸多面体的顶点数是v、棱数是e、面数是f，那么它们总有这样的关系： v - e + f = 2　　①   正多面体的每个面都是正多边形，不妨把边数记为n，而且 n ≥ 3　　② 同时，由于每条棱都属于两个面，故多面体的面数和棱数有以下关系： nf = 2e　　③   每个顶点都是由多条棱相交而成，不妨把与每个顶点相接的棱数记为r。由于顶点是多面体中的顶点，故 r ≥ 3　　④ 否则由两条棱相交的顶点只能是平面图形中的顶点。同时，由于每条棱都连接两个顶点，故多面体的顶点数和棱数有以下关系： rv = 2e　　⑤   把③式和⑤式代入①式，可以得到消掉变量f和v的等式： 2e/r - e + 2e/n = 2， 等式两边同时除以2e可以得到： 1/r - 1/2 + 1/n = 1/e， 即 1/r + 1/n = 1/e + 1/2　　⑥   由于一个正多面体的棱数e至少是6（想想这是为什么），所以⑥式右边最大值为 1/6 + 1/2 = 2/3， 同时，由于棱数e为正数，不论e取何值，⑥式右边一定大于1/2，即 1/2 ＜ ⑥式右边 ≤ 2/3　　⑦ 再由②式和④式可知，r ≥ 3，n ≥ 3。但当 r ≥ 4，n ≥ 4时，⑥式左边≤1/4 + 1/4，即⑥式左边≤1/2，与⑦矛盾。故r和n的取值可分为以下几种情况讨论：

⑴ r ≥ 4时，由于不能同时满足n ≥ 4，而n ≥ 3又必须满足，故此时n = 3。代入⑥式，得1/r = 1/e + 1/6。由于1/r = 1/e + 1/6 ＞ 1/6，故r ＜ 6，故r只能取3、4、5。r = 3，n = 3时代入⑥式和③式得f = 4，此时是一个正四面体；r = 4，n = 3时有f = 8，此时是一个正八面体；r = 5，n = 3时有f = 20，此时是一个正二十面体。   ⑵ 与⑴类似，n ≥ 4时，由于不能同时满足r ≥ 4，而r ≥ 3又必须满足，故此时r = 3。同理可得n只能取3、4、5。r = 3，n = 3时代入⑥式和③式得f = 4，此时是一个正四面体；r = 3，n = 4时有f = 6，此时是一个正六面体（即立方体）；r = 3，n = 5时有f = 20，此时是一个正十二面体。   ⑶ r ≥ 4，n ≥ 4都不满足的时候，又由于r ≥ 3，n ≥ 3，故只能有r = 3，n = 3，此时f = 4，是一个正四面体。

由以上证明可知，三维空间中只存在五种正多面体，分别是正四面体、正六面体、正八面体、正十二面体、正二十面体，当然也就不存在正五面体。