卷积神经网络不同隐藏层卷积核都是一样的吗

Posted 2023-04-29

参考技术A 题主你好，我也是新人，只能发表浅层见解

在训练时可以通过数据库类的transform方法将图像统一变换成相同的大小，比如共同裁剪图像中的200x200的大小，这些图片集作为训练集。

对于卷积核，每一层应该是相同的，因为nn.Conv2d的参数中，kernel size就决定了卷积核大小

以上是我的见解，愿多多指教

理解CNN卷积层与池化层计算

概述

深度学习中CNN网络是核心，对CNN网络来说卷积层与池化层的计算至关重要，不同的步长、填充方式、卷积核大小、池化层策略等都会对最终输出模型与参数、计算复杂度产生重要影响，本文将从卷积层与池化层计算这些相关参数出发，演示一下不同步长、填充方式、卷积核大小计算结果差异。

一：卷积层

卷积神经网络(CNN)第一次提出是在1997年，杨乐春（LeNet）大神的一篇关于数字OCR识别的论文，在2012年的ImageNet竞赛中CNN网络成功击败其它非DNN模型算法，从此获得学术界的关注与工业界的兴趣。毫无疑问学习深度学习必须要学习CNN网络，学习CNN就必须明白卷积层，池化层等这些基础各层，以及它们的参数意义，从本质上来说，图像卷积都是离散卷积，图像数据一般都是多维度数据（至少两维），离散卷积本质上是线性变换、具有稀疏与参数重用特征即相同参数可以应用输入图像的不同小分块，假设有3x3离散卷积核如下：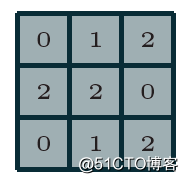

假设有

• 5x5的图像输入块
• 步长为1(strides=1)
• 填充方式为VALID(Padding=VALID)
• 卷积核大小filter size=3x3

则它们的计算过程与输出如下

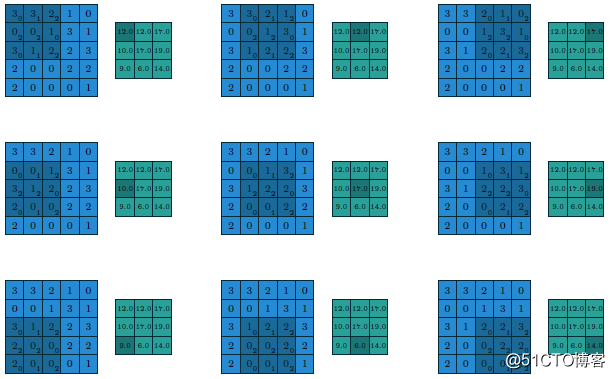
假设这个时候我们修改步长为2、填充方式为SAME，卷积核大小不变(strides=2 Padding=SAME filter size=3x3)，则计算过程与输出变为如下：

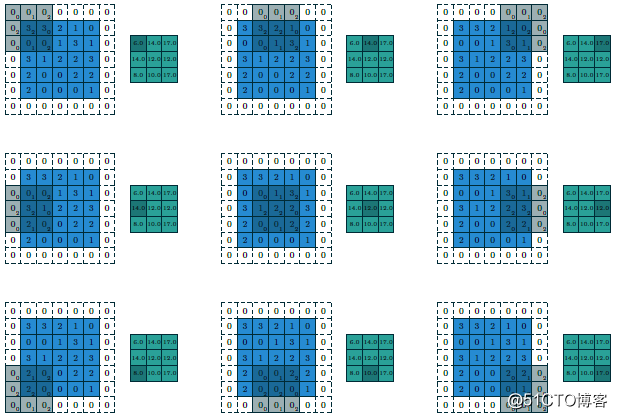
最终输出得到的结果我们可以称为featuremap，CNN的深度多数时候是指featuremap的个数，对多维度的输入图像计算多个卷积核，得到多个featuremap输出叠加，显示如下：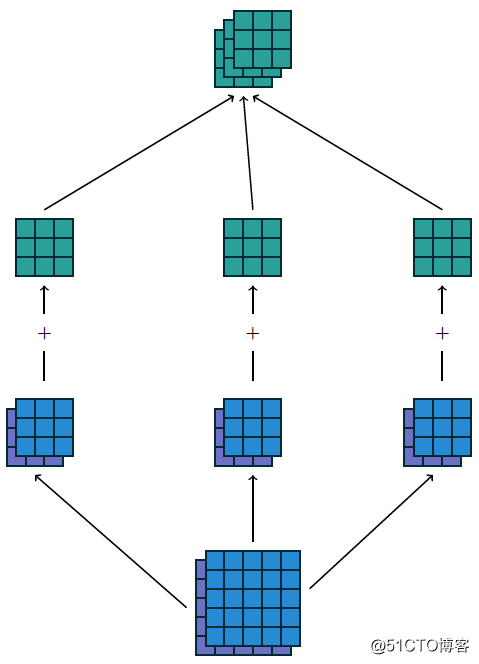

上述输入为5x5x2，使用卷积核3x3，输出3x3x3，填充方式为VALID，计算如果填充方式改为SAME则输出为5x5x3。可以看出填充方式对输出结果的影响。

二：小卷积核VS大卷积核

在AlexNet中有有11x11的卷积核与5x5的卷积核，但是在VGG网络中因为层数增加，卷积核都变成3x3与1x1的大小啦，这样的好处是可以减少训练时候的计算量，有利于降低总的参数数目。关于如何把大卷积核替换为小卷积核，本质上有两种方法。

1.将二维卷积差分为两个连续一维卷积

二维卷积都可以拆分为两个一维的卷积，这个是有数学依据的，所以11x11的卷积可以转换为1x11与11x1两个连续的卷积核计算，总的运算次数：

• 11x11 = 121次
• 1x11+ 11x1 = 22次

2.将大二维卷积用多个连续小二维卷积替代

可见把大的二维卷积核在计算环节改成两个连续的小卷积核可以极大降低计算次数、减少计算复杂度。同样大的二维卷积核还可以通过几个小的二维卷积核替代得到。比如：5x5的卷积，我们可以通过两个连续的3x3的卷积替代，比较计算次数

• 5x5= 25次
• 3x3+ 3x3=18次

三：池化层

在CNN网络中卷积池之后会跟上一个池化层，池化层的作用是提取局部均值与最大值，根据计算出来的值不一样就分为均值池化层与最大值池化层，一般常见的多为最大值池化层。池化的时候同样需要提供filter的大小、步长、下面就是3x3步长为1的filter在5x5的输入图像上均值池化计算过程与输出结果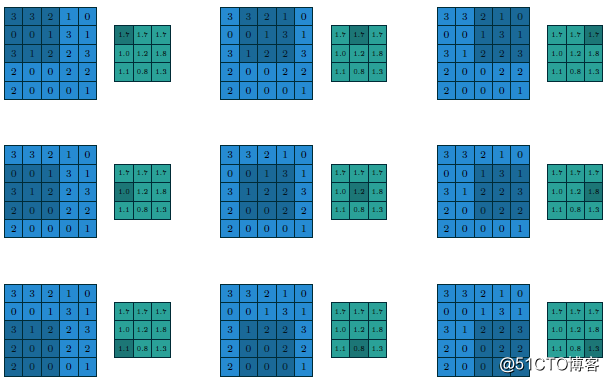

改用最大值做池化的过程与结果如下：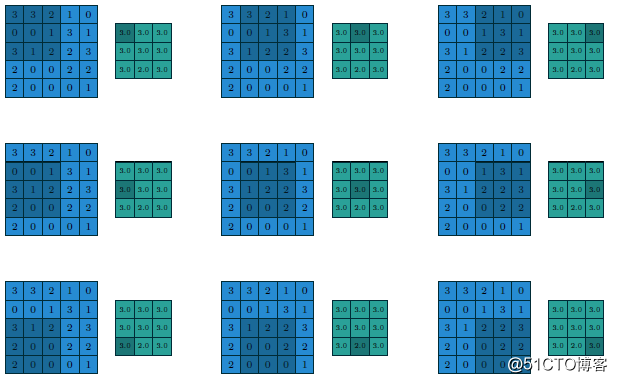

天下难事，
必作于易；
天下大事，
必作于细！

---