理论知识+Python实践 | 在聚类算法中，如何确定类簇的个数？

Posted 2021-04-06 数据科学DataScience

     在对数据集进行聚类分析时，选择最优的类簇个数是至关重要的问题。例如，使用K-means算法聚类时，用户需要指定聚类生成类簇的个数k。我们可以将常用的聚类算法（如K-means，K-medoids/PAM和层次聚类等）分为两类进行讨论。

    （1）直接检验：通过优化某个指标，例如簇内平方和或平均轮廓系数之和。相应的方法分别称为手肘法(Elbow)和轮廓系数法(Silhouette Coefficient)。

    （2）统计检验：会用到统计中的假设推断和分布，Gap Statistic就是其中一种

    首先，导入包和数据，我们使用USArrests(美国拘捕数据)作为演示数据集。读入数据，并将数据标准化以方便比较不同变量。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
%matplotlib inline
# 导入数据
df_original = pd.read_csv('../input/USArrests.csv',index_col=0)
# 将数据标准化
df = (df_original-df_original.mean())/df_original.std()

PART 1

手肘法

   K-means聚类之类的划分方法背后的基本思想是定义类簇，以使总的簇间离散程度（或者说簇间距离平方和）最小化，这衡量了类簇的紧凑性，我们希望它尽可能小。

    手肘法将簇间误差平方和看成是类簇数量k的函数。随着k的增加，每个类簇内的离散程度越小，总距离平方和也就在不断减小，并且减小的程度越来越不明显。极限情况是当k=N时，每个类簇只有一个点，这时总的误差平方和为0。手肘法认为我们应该选择这样的k：当k继续增大时，总误差平方和减少的趋势不再明显，也就是“拐点”处。具体过程如下：

1. 选择一个聚类算法（例如K-means），计算不同k时的聚类结果，例如k可以取为0～10。

2. 对每个k，计算总的簇间距离平方和。

3. 画出总簇间距离平方和随k值增加的变化趋势。

4. 图中弯曲的“拐点”处对应的k就是最合适的类簇数量

      需要注意的是，手肘法有时并不显著。替代方案是平均轮廓系数（Kaufman and Rousseeuw 1990），这个指标同样适用于任何的聚类方法。

代码和结果如下：

SSE = []  # 存放每次结果的误差平方和
for k in range(1,11):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df)
    SSE.append(estimator.inertia_)
X = range(1,11)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.show()

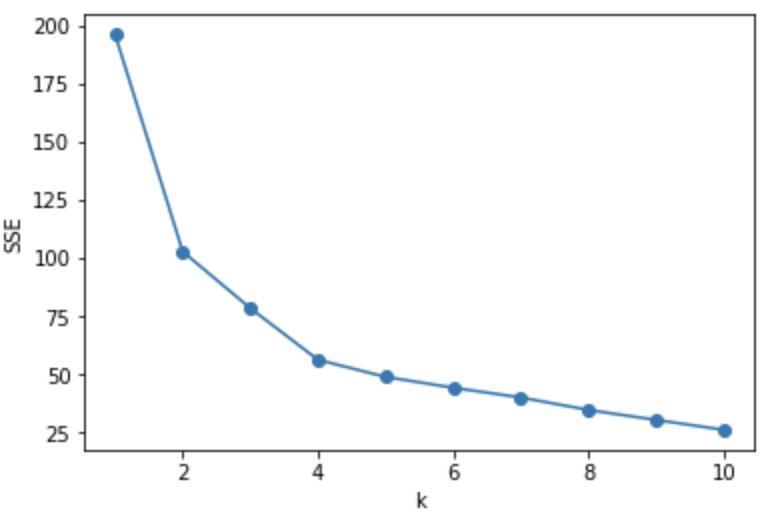
    可以观察到当k=4时是明显的拐点，误差平方和减少的趋势不再明显。所以手肘法的最佳类簇数量是4。

PART 2

平均轮廓系数法

      平均轮廓系数方法衡量了聚类结果的质量，即衡量每个点被放到当前类簇有多合适，平均轮廓系数很高意味着聚类的结果很好。这种方法计算不同k值下，所有点的平均轮廓系数，能够使平均轮廓系数最大的k就是最优的类簇数量（Kaufman and Rousseeuw 1990）。

      具体的过程与手肘法是相似的：

 

1. 选择一个聚类算法（例如K-means），计算不同k时的聚类结果，例如k可以取为0～10。

2. 对于每个k，计算所有观测点的平均轮廓系数。

3. 画出这个指标随着k变化的曲线。

4. 曲线中最高点对应的k就是最优聚类数量。

       代码和结果如下：

from sklearn.metrics import silhouette_score
Scores = [0]  # 存放轮廓系数,根据轮廓系数的计算公式，只有一个类簇时，轮廓系数为0
for k in range(2,11):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df)
    Scores.append(silhouette_score(df,estimator.labels_,metric='euclidean'))
X = range(1,11)
plt.xlabel('k')
plt.ylabel('silhouette')
plt.plot(X,Scores,'o-')
plt.show()

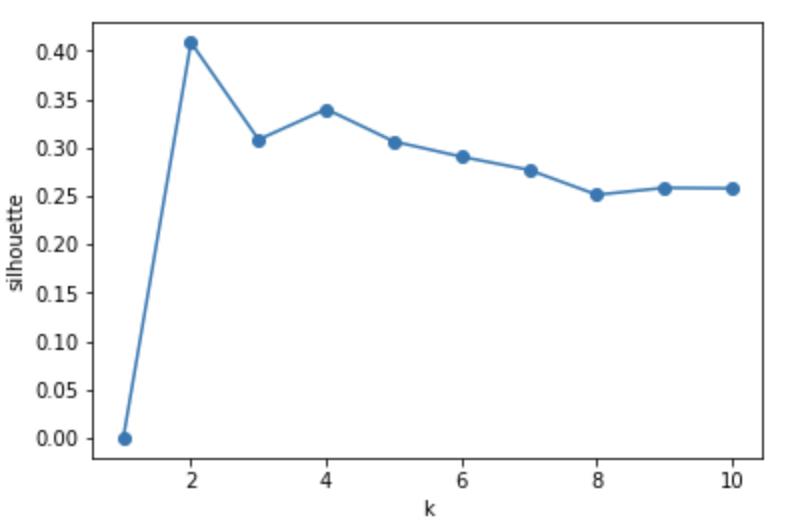
       当k=2时，轮廓系数取最大值，所以选择2作为最优类簇数量。

PART 3

Gap Statistic

      是斯坦福大学的三位教授在2001年的一篇论文中(R. Tibshirani, G. Walther, and T. Hastie, 2001)提出来的，可用于任何的聚类方法。Gap Statistic的主要思想是比较不同k时原始数据的簇内偏差总和与数据在均匀分布推断下的簇内偏差总和。使Gap Statistic这个统计量达到最大值意味着此时的聚类结果结构与随机均匀分布产生的数据的聚类结果差别最大，此时的k就是最优的k。算法如下：

1. 将原始的观测数据进行聚类，k=0,…, k_max，计算不同k值对应的簇内偏离和W_k。

2. 通过随机的均匀分布产生B个推断数据，对这些推断数据进行聚类，k=0,…, k_max。计算不同k值对应的在B个推断数据上的平均簇内偏离和W_kb。

3. 计算gap statistic：W_k与W_kb的log偏差Gap(k)。同时计算这个偏差的标准差sd_k，然后令s_k = sprt(1+1/B*sd_k)。

4. 选择一个最小的k，这样的k满足Gap(k) > Gap(k+1) - s_k+1。

     流行的做法是直接选择最大的Gap(k)所对应的k作为最优k，也就是忽略上述的第四步。需要注意的是当B=500时，W_kb是非常精确的，在下一次迭代中基本保持不变。

代码和结果如下：

# 函数gap_statistic的代码限于篇幅，此处省略，请点击阅读原文
gaps = gap_statistic(df.to_numpy(), 11,50,KMeans)[0]
X = range(1,11)
plt.xlabel('k')
plt.ylabel('Gap Statistic')
plt.plot(X,gaps,'o-')
plt.show()

可以观察到，当k取4时gap值最大，所以4是最优类簇数量。

PART 4

完整Python实现

所有代码和数据都放置在了Kaggle平台：https://www.kaggle.com/pzjzeason/determining-the-optimal-number-of-cluster，复制链接或者点击阅读原文，在电脑上查看该notebook。除了文中介绍的三种方法，也给出了scikit-learn中其他的一些指标。

原文来源：datanovia

原文URL：https://www.datanovia.com/en/lessons/determining-the-optimal-number-of-clusters-3-must-know-methods/

原文标题：Determining-the-optimal-number-of-clusters-3-must-know-methods？

注：作者原文为R代码。

翻译、R代码转Python、排版：彭子健、朝乐门