谁有最小二乘蒙特卡洛方法的美式期权定价python程序代码

Posted 2023-04-20

参考技术A function [c,p]=ucoption(S,X,sigma,r,T,M) sig2=sigma^2; srT=sqrt(T); srTa=sigma*srT; c=0; p=0; for i=1:M ST=S*exp((r-0.5*sig2)*T+srTa*randn); c=c+max(ST-X,0); p=p+max(X-ST,0); end c=c/M; p=p/M; [Call,Put] = blsprice(S, X, r, T, ...本回答被提问者采纳

期权定价模型之Heston模型--参数校准与定价附python代码

Heston模型的校准与定价

前言

在本栏目的文章中，已经介绍了期权定价的数值方法（CRR、MCS等）、经典的BS模型、Merton跳跃扩散模型等经典模型，接下来，在本篇文章中，将系统的介绍Heston模型，并且实现Heston模型的参数校准与定价。

全文代码以Python平台实现，全部代码获取方法如下：
https://download.csdn.net/download/xiaowu1997/74937057

一、Heston模型

由于 Balck-Scholes 模型在假设方面的不足，因此后续的学者不断对 Balck-Scholes 模型进行了修正和改进。

1993 年，Heston[5]提出了随机波动率模型，Heston 模型是 Black-Scholes 模型的延伸。其中，波动率(方差的平方根)不再被假定为常数，方差现在遵循一个随机(CIR)过程。

Heston 模型可以对市场中观察到的隐含波动率进行建模。

HESTON 模型是常见的随机波动率模型，模型假设标的资产价格服从布朗运动，并且将波动率看作一个随机过程。假设标的资产的价格S𝑡和方差V𝑡服从如下扩散过程：

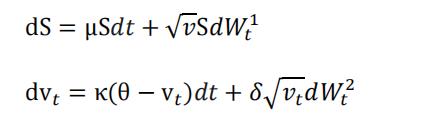
由伊藤引理可知，期权在 t 时刻的价值方差为 C(S,v,t)：

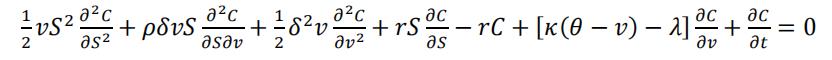
其中，有：

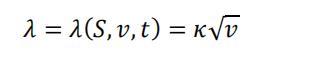
并且上式 满足如下条件：


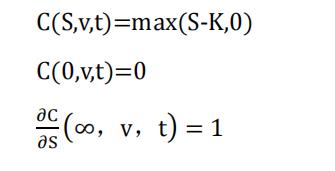
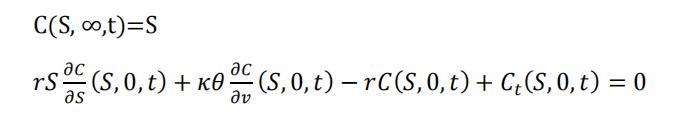
波动率风险𝜆只与波动率有关，因此可以将风险中性情况下
计算出的期权价格应用到实际中，即𝜆 = 0，此时有：

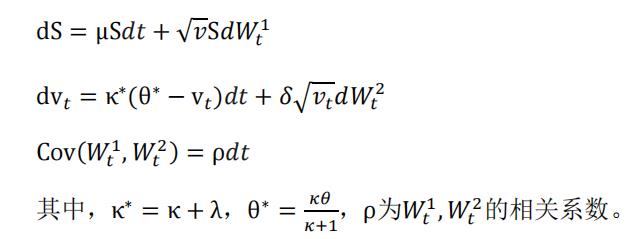
求解以上微分方程可以得到欧式看涨期权的定价公式：

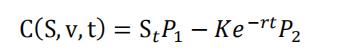
其中：

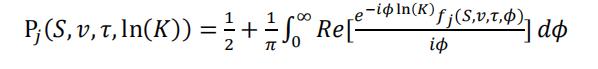
Re[x]为被积函数的实部，i 是虚数单位，并且：

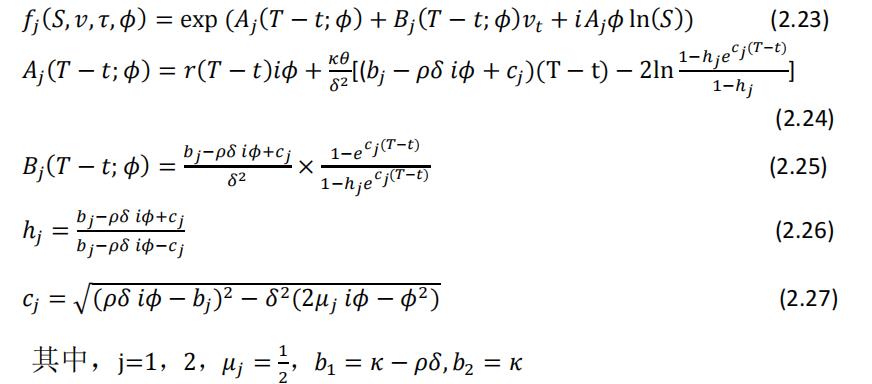
根据看跌-看涨平价公式可知，看跌期权价格为：

二、Heston模型定价实现

Heston模型的部分代码：

def H93_call_value(S0, K, T, r, kappa_v, theta_v, sigma_v, rho, v0):
    ''' Valuation of European call option in H93 model via Lewis (2001)
    Fourier-based approach.

    Parameters
    ==========
    S0: float
        initial stock/index level
    K: float
        strike price
    T: float
        time-to-maturity (for t=0)
    r: float
        constant risk-free short rate
    kappa_v: float
        mean-reversion factor
    theta_v: float
        long-run mean of variance
    sigma_v: float
        volatility of variance
    rho: float
        correlation between variance and stock/index level
    v0: float
        initial level of variance

    Returns
    =======
    call_value: float
        present value of European call option

    '''
    int_value = quad(lambda u: H93_int_func(u, S0, K, T, r, kappa_v,
                                            theta_v, sigma_v, rho, v0),
                     0, np.inf, limit=250)[0]
    call_value = max(0, S0 - np.exp(-r * T) * np.sqrt(S0 * K) /
                     np.pi * int_value)
    return call_value

先对程序进行检验，用一个数值例子求定价过程：

# H93 Parameters
kappa_v = 1
theta_v = 0.05
sigma_v = 0.2
rho = -0.7
v0 = 0.04

S0 = 100
K = 100.0
T = 1
r = 0.05

print("H93 Value   %10.4f"
          % H93_call_value(S0, K, T, r, kappa_v, theta_v, sigma_v, rho, v0))

H93 Value      10.7679

检验完毕，接下来使用上证50期权的数据对Heston模型的参数进行校准，然后用校准的参数进行定价。

三、Heston模型参数校准

根据Heston模型的偏微分方程可知，计算期权价格需要知道

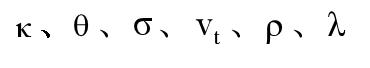
等六个参数的数值，而在风险中性世界中，原来带估参数中的

因此只需求解五个参数即可：

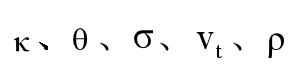
求解思路：

通过求解模型价格和市场价格误差的最小值来估算这些参数，通常这是一个非线性最小二乘优化问题。本研究中，计算期权的模型价格和市场价格的平方误差，然后在整个参数空间中取其最小化：

接下来使用全局最优化和局部最优化算法校准Heston模型的五个参数，这里展示部分代码：

#H93模型校准
import sys
import math
import numpy as np
import pandas as pd
import matplotlib as mpl
from scipy.optimize import brute, fmin

mpl.rcParams['font.family'] = 'serif'
np.set_printoptions(suppress=True,
                    formatter='all': lambda x: '%5.3f' % x)

kappa_r, theta_r, sigma_r = CIR_calibration()

S0 = 4.736 
r0 = 0.015
t=0

# Option Selection
tol = 0.9  # percent ITM/OTM options
options = data[(np.abs(data['行权价'] - S0) / S0) < tol]
options['交易时间'] = pd.DatetimeIndex(options['交易时间'])
options['到期日'] = pd.DatetimeIndex(options['到期日'])
options

%time opt_sv = H93_calibration_full() 

opt_sv#最优参数
array([18.000, 0.026, 0.978, -0.821, 0.035])

四、Heston模型定价分析

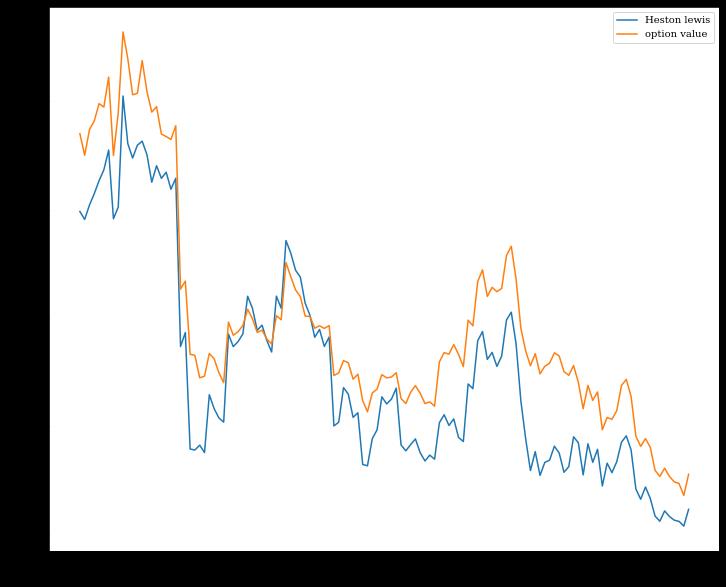
在对参数进行校准后，使用校准的参数进行实证分析，上证50ETF期权定价误差结果分析如下所示：

#参数设置
S0 =data['标的资产价格']  # initial index level
K = 5.25  # strike level
T = data['剩余到期日'] # call option maturity
r = data['无风险利率']/100 # constant short rate
t=0
# H93模型参数
kappa_v = 18
theta_v = 0.026
sigma_v = 0.978
rho =  -0.821
v0 =0.035

label=data['收盘价']
# mape
mape=np.mean(np.abs((pred-label)/label))
# rmse
rmse=np.sqrt(np.mean(np.square(pred-label)))
# mae
mae=np.mean(np.abs(pred-label))
#MSE
mse=np.sum((label-pred)**2)/len(pred)
print('Heston模型测试集的mape:',mape,' rmse:',rmse,' mae:',mae,'MSE:',mse)

Heston模型测试集的mape: 0.6331192663216758  rmse: 0.06059565311773451  mae: 0.04798357142393848 MSE: 0.0036718331767648087

定价结果如图所示：

总结

本章对Heston模型进行了介绍，并且使用sz50ETF期权数据对Heston模型的参数进行校准，并且根据校准的参数对模型进行定价分析。