动态规划的推法 谢谢
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划的推法 谢谢相关的知识,希望对你有一定的参考价值。
各位牛们,麻烦给一个动态规划的推法要领,最好附带一些例子(详细解答)
最好可以用能量项链
推一下max(F[I,K]+F[K+1,J]+tou[i]*wei[k]*wei[j])的动规方程
然后对这个小问题得出最优的答案,并由此推出全局的最优解
1.最优子结构性质;
设Q[i,j]表示第i颗珠子到第j颗珠子合并所产生的能量。显然Q[1,n]表示的是合并产生的总的能量。给定一种标号方法,maxQ[1,n]就是所要求的。设最后一次合并在k处进行,则有Q[1,n]=Q[1,k]+Q[k+1,n]+top[1]*wei[k]*wei[n]。要Q[1,n]最大,必然要Q[1,k],Q[k+1,n]最大。
证明:假设Q[1,k]不是最大,则必然存在一Q'[1,k]>Q[1,k]。那么就有Q'[1,n]=Q'[1,k]+Q[k+1,n]+top[1]*wei[k]*wei[n]>Q[1,k]。这与Q[1,n]的最优性矛盾
能量项链其实就是石子合并
算法分析
竞赛中多数选手都不约而同地采用了尽可能逼近目标的贪心法来逐次合并:从最上面
的一堆开始,沿顺时针方向排成一个序列。 第一次选得分最小(最大)的相邻两堆合并,
形成新的一堆;接下来,在N-1堆中选得分最小(最大)的相邻两堆合并……,依次类推,
直至所有石子经N-1次合并后形成一堆。
例如有6堆石子,每堆石子数(从最上面一堆数起,顺时针数)依次为3 46 5
4 2
(图6.2-5)
要求选择一种合并石子的方案,使得做5次合并,得分的总和最小。
按照贪心法,合并的过程如下:
每次合并得分
第一次合并 3 4 6 5 4 2 5
第二次合并 5 4 6 5 4 9
第三次合并 9 6 5 4 9
第四次合并 9 6 9 15
第五次合并 15 9 24
24
总得分=5+9+9+15+24=62
但是当我们仔细琢磨后,可得出另一个合并石子的方案:
每次合并得分
第一次合并 3 4 6 5 4 2 7
第二次合并 7 6 5 4 2 13
第三次合并 13 5 4 2 6
第四次合并 13 5 6 11
第五次合并 13 11 24
24
总得分=7+6+11+13+24=61
显然,后者比贪心法得出的合并方案更优。 题目中的示例故意造成一个贪心法解题的
假像,诱使读者进入“陷阱”。为了帮助读者从这个“陷阱”里走出来, 我们先来明确一
个问题:
1.最佳合并过程符合最佳原理
使用贪心法至所以可能出错, 是因为每一次选择得分最小(最大)的相邻两堆合并,
不一定保证余下的合并过程能导致最优解。聪明的读者马上会想到一种理想的假设:如果N
-1次合并的全局最优解包含了每一次合并的子问题的最优解,那么经这样的N-1次合并后
的得分总和必然是最优的。
例如上例中第五次合并石子数分别为13和11的相邻两堆。 这两堆石头分别由最初
的第1,2,3堆(石头数分别为3,4,6)和第4,5,6堆(石头数分别为5,4,
2)经4次合并后形成的。于是问题又归结为如何使得这两个子序列的N-2 次合并的得分
总和最优。为了实现这一目标,我们将第1个序列又一分为二:第1、2堆构成子序列1,
第3堆为子序列2。第一次合并子序列1中的两堆,得分7; 第二次再将之与子序列2的
一堆合并,得分13。显然对于第1个子序列来说,这样的合并方案是最优的。同样,我
们将第2个子序列也一分为二;第4堆为子序列1,第5,6堆构成子序列2。第三次合
并子序列2中的2堆,得分6;第四次再将之与子序列1中的一堆合并,得分13。显然
对于第二个子序列来说,这样的合并方案也是最优的。 由此得出一个结论——6堆石子经
过这样的5次合并后,得分的总和最小。
我们把每一次合并划分为阶段,当前阶段中计算出的得分和作为状态, 如何在前一次
合并的基础上定义一个能使目前得分总和最大的合并方案作为一次决策。很显然,某阶段
的状态给定后,则以后各阶段的决策不受这阶段以前各段状态的影响。 这种无后效性的性
质符最佳原理,因此可以用动态规划的算法求解。
2.动态规划的方向和初值的设定
采用动态规划求解的关键是确定所有石子堆子序列的最佳合并方案。 这些石子堆子序
列包括:
{第1堆、第2堆}、{第2堆、第3堆}、……、{第N堆、第1堆};
{第1堆、第2堆、第3堆}、{第2堆、第3堆、第4堆}、……、{第N堆、第1
堆、第2堆};
……
{第1堆、……、第N堆}{第1堆、……、第N堆、第1堆}……{第N堆、第1堆、
……、第N-1堆}
为了便于运算,我们用〔i,j〕表示一个从第i堆数起,顺时针数j堆时的子序列
{第i堆、第i+1堆、……、第(i+j-1)mod n堆}
它的最佳合并方案包括两个信息:
①在该子序列的各堆石子合并成一堆的过程中,各次合并得分的总和;
②形成最佳得分和的子序列1和子序列2。由于两个子序列是相邻的, 因此只需记住
子序列1的堆数;
设
f〔i,j〕——将子序列〔i,j〕中的j堆石子合并成一堆的最佳得分和;
c〔i,j〕——将〔i,j〕一分为二,其中子序列1的堆数;
(1≤i≤N,1≤j≤N)
显然,对每一堆石子来说,它的
f〔i,1〕=0 c〔i,1〕=0 (1≤i≤N)
对于子序列〔i,j〕来说,若求最小得分总和,f〔i,j〕的初始值为∞; 若求最大得
分总和,f〔i,j〕的初始值为0。(1≤i≤N,2≤j≤N)。
规划的方向是顺推。先考虑含二堆石子的N个子序列(各子序列分别从第1堆、第2堆、
……、第N堆数起,顺时针数2堆)的合并方案
f〔1,2〕,f〔2,2〕,……,f〔N,2〕
c〔1,2〕,c〔2,2〕,……,c〔N,2〕
然后考虑含三堆石子的N个子序列(各子序列分别从第1堆、第2堆、……、第N堆
数起,顺时针数3堆)的合并方案
f〔1,3〕,f〔2,3〕,……,f〔N,3〕
c〔1,3〕,c〔2,3〕,……,c〔N,3〕
……
依次类推,直至考虑了含N堆石子的N个子序列(各子序列分别从第1堆、第2堆、 …
…、第N堆数起,顺时针数N堆)的合并方案
f〔1,N〕,f〔2,N〕,……,f〔N,N〕
c〔1,N〕,c〔2,N〕,……,c〔N,N〕
最后,在子序列〔1,N〕,〔2,N〕,……,〔N,N〕中,选择得分总和(f值)最
小(或最大)的一个子序列〔i,N〕(1≤i≤N),由此出发倒推合并过程。
3.动态规划方程和倒推合并过程
对子序列〔i,j〕最后一次合并,其得分为第i堆数起,顺时针数j堆的石子总数t。被
合并的两堆石子是由子序列〔i,k〕和〔(i+k-1)modn+1,j-k〕(1≤k≤j-1)
经有限次合并形成的。为了求出最佳合并方案中的k值,我们定义一个动态规划方程:
当求最大得分总和时
f〔i,j〕=max{f〔i,k〕+f〔x,j-k〕+t}
1≤k≤j-1
c〔i,j〕=k│ f〔i,j〕=f〔i,k〕+f〔x,j-k〕+t
(2≤j≤n,1≤i≤n)
当求最小得分总和时
f〔i,j〕=min{f〔i,k〕+f〔x,j-k〕+t}
1≤k≤j-1
c〔i,j〕=k│ f〔i,j〕=f〔i,k〕+f〔x,j-k〕+t
(2≤j≤n,1≤i≤n)
其中x=(i+k-1)modn+1,即第i堆数起,顺时针数k+1堆的堆序号。
例如对(图6.2-4)中的6堆石子,按动态规划方程顺推最小得分和。 依次得出含
二堆石子的6个子序列的合并方案
f〔1,2〕=7 f〔2,2〕=10 f〔3 ,2〕=11
c〔1,2〕=1 c〔2,2〕=1 c〔3,2〕=1
f〔4,2〕=9 f〔5,2〕=6 f〔6,2〕=5
c〔4,2〕=1 c〔5, 2〕=1 c〔6,2〕=1
含三堆石子的6个子序列的合并方案
f〔1,3〕=20 f〔2,3〕=25 f〔3,3〕=24
c〔1,3〕=2 c〔2,3〕=2 c〔3,3〕=1
f〔4,3〕=17 f〔5,3〕=14 f〔6,3〕=14
c〔4,3〕=1 c〔5,3〕=1 c〔6,3〕=2
含四堆石子的6个子序列的合并方案
f〔1,4〕=36 f〔2,4〕=38 f〔3,4〕=34
c〔1,4〕=2 c〔2,4〕=2 c〔3,4〕=1
f〔4,4〕=28 f〔5,4〕=26 f〔6,4〕=29
c〔4,4〕=1 c〔5,4〕=2 c〔6,4〕=3
含五堆石子的6个子序列的合并方案
f〔1,5〕=51 f〔2,5〕=48 f〔3,5〕=45
c〔1,5〕=3 c〔2,5〕=2 c〔3,5〕=2
f〔4,5〕=41 f〔5,5〕=43 f〔6,5〕=45
c〔4,5〕=2 c〔5,5〕=3 c〔6,5〕=3
含六堆石子的6个子序列的合并方案
f〔1,6〕=61 f〔2,6〕=62 f〔3,6〕=61
c〔1,6〕=3 c〔2,6〕=2 c〔3,6〕=2
f〔4,6〕=61 f〔5,6〕=61 f〔6,6〕=62
c〔4,6〕=3 c〔5,6〕=4 c〔6,6〕=3
f〔1,6〕是f〔1,6〕,f〔2,6〕,……f〔6,6〕中的最小值,表明最小
得分和是由序列〔1,6〕经5次合并得出的。我们从这个序列出发, 按下述方法倒推合
并过程:
由c〔1,6〕=3可知,第5次合并的两堆石子分别由子序列〔1,3〕和子序列〔
4,3〕经4次合并后得出。其中
c〔1,3〕=2可知由子序列〔1,3〕合并成的一堆石子是由子序列〔1,2〕和
第三堆合并而来的。而c〔1,2〕=1,以表明了子序列〔1,2〕的合并方案是第1堆
合并第2堆。
由此倒推回去,得出第1,第2次合并的方案
每次合并得分
第一次合并 3 4 6…… 7
第二次合并 7 6…… 13
13……
子序列〔1,3〕经2次合并后合并成1堆, 2次合并的得分和=7+13=20。
c〔4,3〕=1,可知由子序列〔4,3〕合并成的一堆石子是由第4堆和子序列〔5,
2〕合并而来的。而c〔5,2〕=1,又表明了子序列〔5,2〕的合并方案是第5堆合
并第6堆。由此倒推回去,得出第3、第4次合并的方案
每次合并得分
第三次合并 ……54 2 6
第四次合并 ……5 6 11
……11
子序列〔4,3〕经2次合并后合并成1堆,2次合并的得分和=6+11=17。
第五次合并是将最后两堆合并成1堆,该次合并的得分为24。
显然,上述5次合并的得分总和为最小
20+17+24=61
上述倒推过程,可由一个print(〔子序列〕)的递归算法描述
procedure print (〔i,j〕)
begin
if j〈〉1 then {继续倒推合并过程
begin
print(〔i,c〔i,j〕);{倒推子序列1的合并过程}
print(〔i+c〔i,j〕-1)mod n+1,j-c〔i,j〕)
{倒推子序列2的合并过程}
for K:=1 to N do{输出当前被合并的两堆石子}
if (第K堆石子未从圈内去除)
then begin
if(K=i)or(K=X)then置第K堆石子待合并标志
else第K堆石子未被合并;
end;{then}
第i堆石子数←第i堆石子数+第X堆石子数;
将第X堆石子从圈内去除;
end;{then}
end;{print}
例如,调用print(〔1,6〕)后的结果如下:
print(〔1,6〕)⑤
│
┌——————┴——————┐
│ │
print(〔1,3〕)② print(〔4,3〕)④
│ │
print(〔1,2〕)① ┌—————┴—————┐
│ │ │
│
┌—————┴—————┐ print(〔4,1〕) print(〔5,2〕)③
│ │ │
print(〔1,1〕) print(〔2,1〕) │
┌——————┴——————┐
│ │
print(〔5,1〕) print(〔6,1〕)
(图6.2-5)
其中回溯至
① 显示 3 46 5 4
② 显示 7 65 4 2
③ 显示 13 54 2
④ 显示 135 6
⑤ 显示 13 11
注:调用print过程后,应显示6堆石子的总数作为第5次合并的得分 参考技术A 动态规划与排列组合2008-06-06 09:00 作者: 刘未鹏|C++的罗浮宫 出处: 天极网 责任编辑:>dizzarz 像所有的新手一样,对一种算法思想的理解需要经历从肤浅(流于表面形式)到逐渐触摸到本质的过程。为什么说"逐渐"触摸到本质,是因为很多时候你并不确定一个解释是不是最本质的,有时候会有好几个等价的解释,各自在不同的场景下具有启发。
比如对动态规划(DP)的理解,一开始我理解为"递推",但实际上这是最肤浅的理解,对于如何在特定的问题中找到递推关系毫无帮助和启发。换言之,这只是一个描述性的总结,而不是一个建设性的总结,不含方法论。
做(看)了一些题目之后我开始总结关于"How"的方法,怎样寻找到递推关系(递推关系蕴含着子问题)。得到一个简单的观察,如果一个问题里面含有n这个变量,考虑把n变成n-1的情况。
当然,这个方法是非常特殊(狭窄)的。实际上更具一般性的方法是不仅可以从n-1后面切一刀,还可以在任意地方切(譬如切成两个n/2规模的),以任意标准切(比如像快排那样的)。所有考虑各种切法中哪种能够最有利于建立子问题是有帮助的。
这个我姑且把它叫做通过直接切分问题来寻找子问题。
可是。这还是特殊了。因为显然这个方法不能解决所有的DP问题,连"多数"DP问题都未必能解决。譬如大家熟悉的"最大(小)和连续子序列"问题,就难以通过这种方法求解(可行,但思维难度较大。);再譬如上次Lee给的敲石头问题,以及DD出的不听话的机器人问题。因此,在知道了这几个问题的解法之后我继续思考这些解法里面是不是蕴含着更具一般性的解题方法。
看起来我找到了一个,就是分类讨论法,具体做法是:首先,写出可行解的一般形式,譬如a1, a2, ..., an。然后对其中的某个不确定的ai进行讨论。譬如旅行商问题里面对"下一个城市"进行讨论。当不确定时,讨论。讨论的每个分支都带来了进一步的确定性,从而将问题转化成一个子问题。
然后Lee提到,这个方法是自顶向下的,有时候不适于思考,譬如对敲石头问题。并提到一种自底向上,着重于构造"状态"的外推法。
于是,到目前为止,DP的一般性启发式思考方法就已经有了三种:
1. 通过直接对问题切分来探索子问题。
2. 通过对可行解的分类讨论来探索子问题。
3. 通过建立"状态"来自底向上地推导最终解。
可是,我心里还是不踏实,因为"离散"的知识是极其不利于记忆的,需要更多的练习才能在运用的时候"不由自主"的联想起来,而且也容易遗忘。每次做DP题的时候,我都得把好几种指导性的思路一一费劲从脑袋里翻出来,然后尝试。实在很不爽。虽然DP题也许并没有万用的解题手法,但我还是希望能够尽量提取出不同手法之间的本质联系,如果能够将一组看上去离散的知识点统一在一个更具一般性,更本质的知识点下面,我们的知识树就多出了一个根节点,于是下次提取的时候只要提取出那个根节点,下面的几个子节点就会一一乖乖闪现,极大的降低记忆的复杂性。
那么,上面三种手法的本质联系到底是什么呢?有一次在路上走的时候我想出了一种解释。它也许不是最本质的,也许大牛们早就想到过,但是我觉得至少有两个好处:
1. 它涵盖以上三种手法,通过增加一个根节点,减少知识的记忆复杂性和易提取性。
2. 归纳抽象的过程本身就是一种锻炼,锻炼的是归纳抽象的能力。
这个解释就是:大多DP问题的可行解的形式是一个排列组合(典型的——旅行商问题、最短路径问题)。大家都知道,穷举一个规模为N的排列组合复杂性是a^n的,也就是"组合复杂性"。而求解DP问题的核心步骤:发现“子问题”,这个“子问题”实际上就是对应最终解的那个排列组合的某个"子排列组合"(某种子集);而这里的“子排列组合”的数目则往往是多项式的(silwile,XuYou,g9指出并非总是如此),这就是为什么一个组合复杂性的穷举问题可以DP优化为多项式复杂度的问题。将重复出现的子排列组合对应的子问题的解缓存起来,就是DP的缓存优化了。
此外,这一解释也提供了如何探索子问题的一个通用方案:寻找形式相同的子排列组合。还是拿最大和连续子序列说事,其解的形式是:A[i], A[i+1], .., A[j-1], A[j],其中i,j不确定。那么如何得到形式相同的子组合呢?首先讨论A[j],为什么要讨论,因为只要A[j]不确定,A[j-1]就不确定,就拿不出子组合来。对于一个确定的A[j0],解的可能性为A[i], A[i+1], .., A[j0-1], A[j0]。其最优解依赖于子组合A[i], A[i+1], .., A[j0-1],到这里子问题就不请子现了:A[i], A[i+1], .., A[j0-1], A[j0]和A[i], A[i+1], .., A[j0-1]的形式相同,意味着它们是同一个问题的不同阶表示。
当然,由于这个指导思想一般性大了点,所以实际问题中往往没有前面提到的三种手法寻找方案来得快——众所周知的是,越特定的手法解题面虽然越窄,但如果题目对口了解决起来也越快。但它至少有两个好处(前面说过了)。所以考虑一般性和特殊性的手法都是有帮助的。
类似的,敲石头问题也可以通过这种手法来探索子问题。至少目前我做过的DP题似乎都可以借助这种手法来探索,当然,刚才说过了,未必是最快的,所以也许可以考虑用来做后备方案,当其它方案没有头绪的时候试试。
我的解题经验还很有限,所以不清楚这个手法的覆盖范围有多广。实际上一个更广的领域是"组合优化"。更上面提到的很像。但针对的问题就不仅止于DP了。
参考
1. 《Introduction To Algorithms》的DP章节。
2. 《Algorithms》的DP章节。
3. 《Algorithm Design Manual》的DP章节。
4. DD的《背包问题九讲》
5. wikipedia
6. 网络搜索出来的一堆题目和讲解。(如《动态规划经典题集》)
7. TopLanguage上的帖子:矩阵也疯狂、DPDP、DPDP(二)
http://www.google.cn/search?hl=zh-CN&q=%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%9A%84%E6%8E%A8%E6%B3%95%E8%A6%81%E9%A2%86&btnG=Google+%E6%90%9C%E7%B4%A2&meta=&aq=f&oq=
再看看这个网页第二资源 很是不错本回答被提问者采纳 参考技术B 应该使用lingo来解吧,matlab解有点麻烦! 参考技术C 看吧http://www.zsqz.com/jsbase/suanfa/dtguihua/chapter9_2.htm
算法 动态规划 ------最长公共子序列
这篇博客是我 听完这位老师讲完课的 记录。https://www.youtube.com/watch?v=mgDUoITB24I&t=645s 还有我个人的理解,如果有错误或者有争议的地方,欢迎留言。谢谢大家~

子序列 就是说 从原有列表中按照出现先后顺序从中选择部分 元素 组成的新的列表。

最长公共子序列的含义: 选择两个列表中公共的子序列的最大长度,这个子序列即为最长公共子序列。

用蛮力的方法求解,对于长度为 M的 列表,它所有的子序列的个数有 2^m ,每个元素有两种情况,被选入子序列或者不被选入。

接下来是 动态规划中非常重要的问题,子问题的界定。 对于 长度分别为 M, N的 子列表, 原始的问题是 长度 为 M,N两个子序列的最长子序列,那么,子问题是 对于 长度为M的子序列,我们取 X1到 Xi, 对于长度为 N的子序列,我们取 Y1到 Yj, 那么,由这个子问题界定的范围就是 上图中黄色区域所包括的范围。
在这里,我们看到子问题也有两个参数,一个是代表 x的最后的位置,一个是代表 y的最后的位置。这是两个不同序列的参数。
现在考虑 子问题 和 大问题 有着怎么样的依赖关系。

递推方程:

注意,我们的目标是 求得最长的公共子序列,所以,当子问题中的两个序列最后的字符不相同,那么,我们就要 裁出 其中的一部分, 同时,要选择 使 子序列长度最大的区间走。
标记函数的目标是 追踪我们找到的最长子序列的路径。 我们最开始存的是最长公共子序列的最后那个元素。
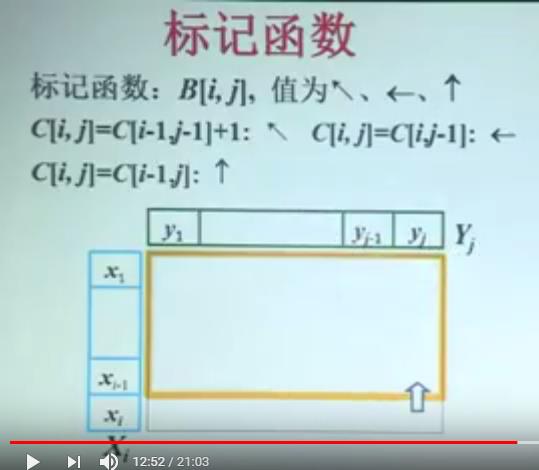

注意: 我们的 C[i,j]存的是 子序列的长度,当 序列X或序列Y的长度为0,那么,最长的公共子序列的长度 C[i,j]当然为0
得到结果后,开始追踪解,也就是获得最长的公共子序列具体是哪些元素。

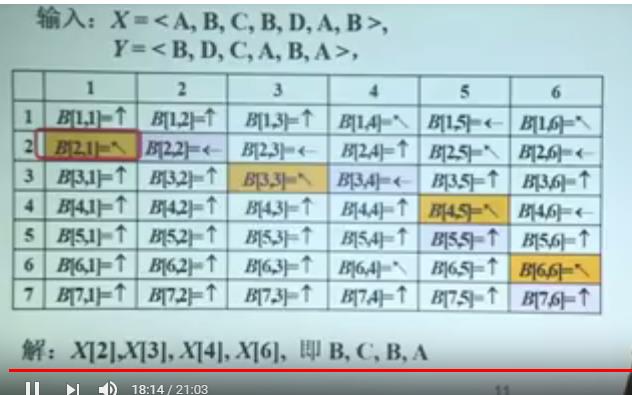
来来来,看老师在课上给的例子。
讨论下复杂度。空间+时间

最后老师的总结:

具体的代码 下次贴咯,在图书馆,窗外下着小雨。学校广播台在放着不知名的音乐,是点歌节目。
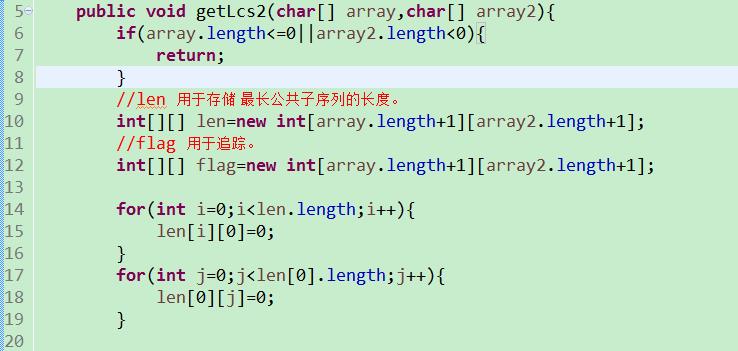
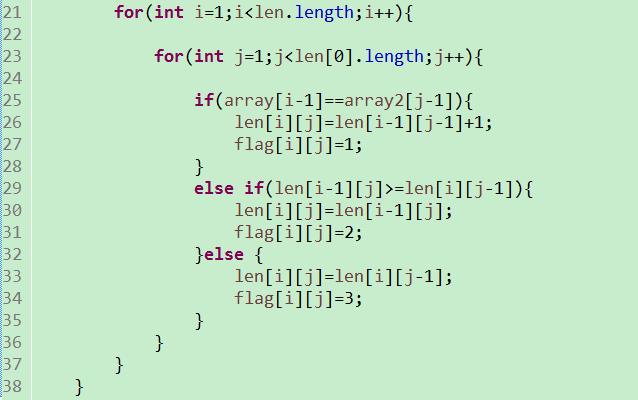
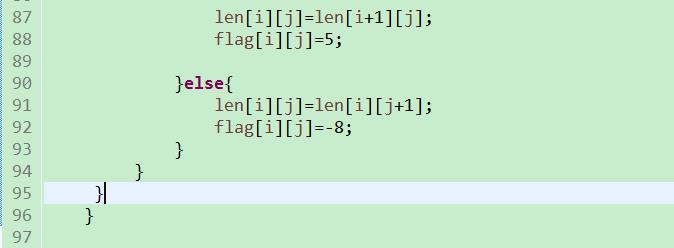
代码:
还可以从 底部开始:

以上是关于动态规划的推法 谢谢的主要内容,如果未能解决你的问题,请参考以下文章
利用动态规划求解旅行商问题(Travelling Salesman Problem)时空复杂度分析以及相关实验验证
《每日一题》之第五十八题考查知识点:资源分配的动态规划问题(题源自广东工业大学18年真题第九大题)(图一为昨天题目答案)