利用动态规划求解旅行商问题(Travelling Salesman Problem)时空复杂度分析以及相关实验验证

Posted 2021-04-18 数据魔术师

      利用动态规划求解旅行商问题（Travelling Salesman Problem，简称TSP）在之前的推文中已经有了详细的介绍，今天我们要对这个问题进行更深一步的探索，即随着问题规模的变化，使用动态规划算法求解TSP耗费的时间是多少？耗费的计算机内存又是多少？这都值得我们进一步去探索，为此，我们特地做了一组实验来探索上面的问题。我们实验中使用的计算机的配置如下：

 先给出之前推文的链接：

        

       首先对于之前写的代码的时间复杂度（执行算法所需要的计算工作量）进行理论分析，核心代码如下：

double slove(){
    int M = (1 << N);
    dp[1][0] = 0;
    for (int i = 1; i < M; i ++){
        for (int j = 1; j < N; j ++){
            if (i & (1 << j)) continue;
            if (!(i & 1)) continue;
            for (int k = 0; k < N; k ++){
                if (i & (1 << k)){
                    dp[(1 << j) | i][j] = min(dp[(1 << j) | i][j], dp[i][k] + dis[k][j]);
                }
            }
        }
    }
    for (int i = 0; i < N; i ++)
        ans = min(dp[M - 1][i] + dis[i][0], ans);
    return ans;
}

        抛开复杂的时间复杂度分析理论不谈，我们知道一般一层for循环就是一个乘数，把每个嵌套的循环次数乘起来最大的那个就是我们的时间复杂度。所以我们上面的代码的时间复杂度应该是O（MN^2），其中N是给定算例的点的个数，而M = 2^N，所以总体的时间复杂度为O(N^2*2^N)，是一个指数级的时间复杂度，随着N的增大，其时间代价会顺势快速增长。

       为了进一步表现这个时间复杂度的可怕之处，我们令N，也就是完全图中的点的个数，从3变到30生成28个随机算例，做出来的时间图像大概是这样：

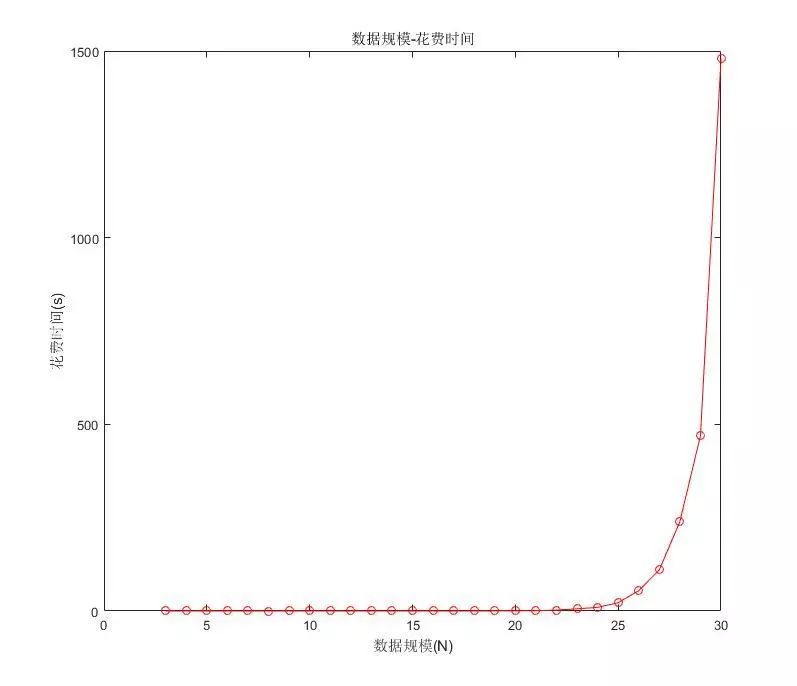
由此可见，指数级的算法时间增长还是相当恐怖的。

      但是，同时我们要清楚，利用动态规划求解TSP 的空间复杂度(是对一个算法在运行过程中临时占用存储空间大小的量度)同样也是O(N^2*2^N)，为此，我们特地测试了同等规模算例的空间使用情况，大概的图像就是这样：

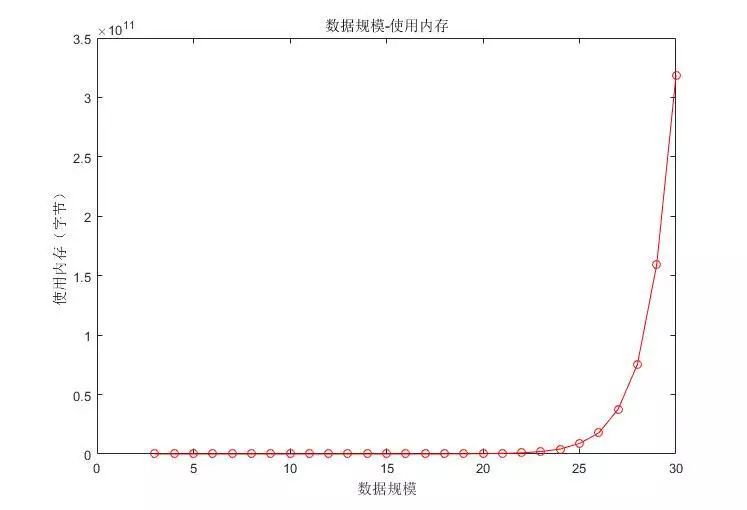
我们使用的计算机最大内存为480G（可以说配置相当高了）。但是，当数据规模达到31个服务点的时候，仍然出现了内存溢出的情况，因此我们制作了如下图的表格来更清晰的表现实验的状况。

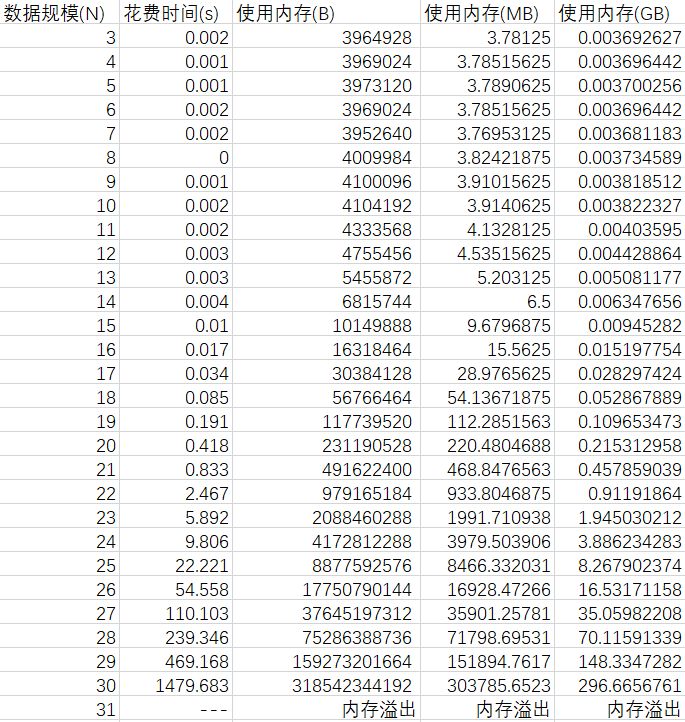
       可以看出，在数据规模较小的时候，算法消耗的时间和空间甚至都可以忽略不计，但是随着问题规模的扩大，时间和空间消耗都到达了难以忍受的地步。

欲下载与本文相关的代码和测试数据，请移步留言区。

【如对代码有疑问，可联系小编，可以提供有偿辅导服务】

【有偿辅导纯属个人行为，与团队无关】

 赞 赏 

长按下方二维码打赏

感谢您，

支持学生们的原创热情！

郑重承诺

打赏是对工作的认可

所有打赏所得

都将作为酬劳支付给辛勤工作的学生

指导老师不取一文

 

 

精彩文章推荐

-The End-

文案 / 贺兴（大四）

排版 / 贺兴（大四）

代码 / 贺兴（大四）

审核 / 贺兴（大四）

指导老师 / 秦时明岳

---

如对代码有疑问，可联系小编，可以提供有偿辅导服务。PS:部分资料来自网络。

贺兴（华中科技大学管理学院本科四年级、[e-mail])