多元回归：理解机器学习

Posted 2021-04-03 使用Python玩转数学

案例内容：建立人口自然增长率预测模型。在建立预测模型的过程中，理解卡内基梅隆大学教授Tom Mitchell教授对机器学习的定义，机器学习由目标任务T、经验数据E及性能度量P构成。

通过编写简单回归案例，我们现在已经了解了编写机器学习程序的基本过程。若把机器学习的目的看作是任务，完成该任务首先要准备数据集，数据集由训练和测试两个数据集构成，然后再设计一个学习算法，该算法从训练集的数据中学习，找出与任务适配的模型，还要设计一个度量模型性能的方法，用来度量模型在任务上完成的质量。

通过身高来预测体重的回归案例，初步了解了编写机器学习程序的过程。但对于初次接触机器学习的读者来说，它还是一个比较深奥、抽象化的概念。虽然概念很抽象，不过人们每天都或多或少与机器学习系统（把机器学习定义为系统会更好一些，因为它是有若干部分构成的）打过交道。

例如：刷脸支付就是一个机器学习系统，它会记住人脸表情的每一次变化，防止识别错误或使用照片来模拟人脸，人脸检测是机器学习视觉领域被深入研究的一个问题。

再如：人们经常使用的翻译工具（如百度翻译、谷歌翻译等）也是一个机器学习系统，它学习的数据是语料库（语料库存放的是在语言实际使用中真实出现过的语言材料），生成翻译统计模型，由模型完成句子的翻译。

卡内基梅隆大学教授Tom Mitchell在他所著的《机器学习》一书里为机器学习给出了一个简洁的定义：“对于某类任务T和性能度量P，一个计算机程序被认为可以从经验E中学习是指通过经验E改进后，它在任务T上由性能度量P衡量的性能有所提升”。

任务T可以理解为机器学习程序要实现的目标，如通过身高预测体重是程序要实现的目标、把中文自动翻译成英文是程序要实现的目标等待。

程序要实现任务T的目标，需要从经验E中学习，学习过程不能算是任务，学习是程序获取完成任务的能力，即建立与任务目标适配的模型。对于通过身高预测体重任务来说，建立回归预测模型；对于自动翻译任务来说，建立翻译统计模型。

经验E为已经量化的与任务相关的特征数据，如前面回归案例的训练数据集train_hw.csv，数据集存储了经过测量的身高和体重，身高和体重就是特征数据，身高和体重都已经标量化（纯数值）。程序处理这些数据时，会将这些数据表示成一个向量，向量的每个分量是一个特征数据。

为了度量模型的性能，还需要设计性能度量P，用来评估模型工作的准确性。性能度量P也是一个程序，程序的输入是测试数据集，因为我们更加关注模型在未观测数据上的性能如何，因为这将决定机器学习程序在实际应用中的性能。

下面通过一个多元回归案例，深入理解机器学习。

任务目标

案例任务T目标是为中国人口自然增长率建立预测模型，该模型根据国民总收入、人均GDP和居民消费价格指数三个因素来预测中国人口自然增长率，这三个因素也称为样本特征。

数据准备

要实现案例任务T的目标，需要通过学习算法从经验E中建立预测模型，经验E为国民总收入、人均GDP和居民消费价格指数及人口自然增长率数据集，下表列出了该数据集的内容：

经验E的数据在程序中一般使用向量来表示，使用Numpy的数组可以表示向量。

例如：

>>> import numpy as np
>>> v = np.array([15.73,15037,1366,18.8])

上面的代码创建了向量v，v存储了上表的第1条记录（数据集的第1个样本，年份字段除外）。若要存储全部样本数据，可以使用Numpy二维数组来存储样本数据。

例如：

import numpy as np
M = np.array([
    [15.73,15037,1366,18.8],
    [15.04,17001,1519,18],
    ……
    [5.28,215904,16500,15]
    ])

上面的代码创建了矩阵M，M是20 X 4的矩阵，M的每一行是一个样本，M的每一列对应数据集的不同特征，如第1列是人口自然增长率，第2列是国民总收入，第3列是人均GDP，第4列是消费价格指数。

学习算法设计

有了经验数据E，就要考虑设计学习算法了。学习算法是从经验数据E中找出数据集变量间的函数关系，即建立预测模型（函数模型）。

在身高预测体重案例中，其数据集有两个变量：身高和体重，体重是因变量，身高是自变量，建立的函数关系是一元一次函数，变量间的关系是线性关系。

在预测人口自然增长率案例的数据集中，有四个变量，其中人口自然增长率是因变量，国民总收入、人均GDP、消费价格指数是自变量，学习算法要建立的函数关系是多元函数，是多元一次函数，还是多元二次函数，……，需要我们通过散点图来发现因变量与多个自变量间的关系。

例1  绘制因变量与自变量散点图

# 导入numpy库
import numpy as np
import matplotlib.pyplot as plt
  
  
# 定义绘图函数
def plotter(ax, data1, data2, param_dict,type):
    if type == 0:
       ax.scatter(data1,data2,**param_dict)
    else:
       ax.plot(data1, data2, **param_dict)
   
  
  
# 程序入口
if __name__ == '__main__':
  
   # 设置图例中文显示
   plt.rcParams['font.sans-serif'] = ['SimHei']
  
   # 读取训练集
   data = np.genfromtxt('train_population.csv',delimiter=',',dtype='float')
   # 人口增长率为因变量
   y = data[::,1]
   # 创建4个子轴
   fig, ax = plt.subplots(2, 2)
   # 绘制人口增长率与GDP散点图
   x = data[::,2]
   plotter(ax[0][0],x,y,{'color': 'b','label':'人口增长率与国民总收入'},0)
   ax[0][0].legend()
   # 绘制人口增长率与GDP散点图
   x = data[::,3]
   plotter(ax[0][1],x,y,{'color': 'm','label':'人口增长率与人均GDP'},0)
   ax[0][1].legend()
   # 绘制人口增长率与消费价格指数散点图
   x = data[::,4]
   plotter(ax[1][0],x,y,{'color': 'm','label':'人口增长率与消费价格指数'},0)
   ax[1][0].legend()
   plt.show()

绘制的散点图如下图所示：

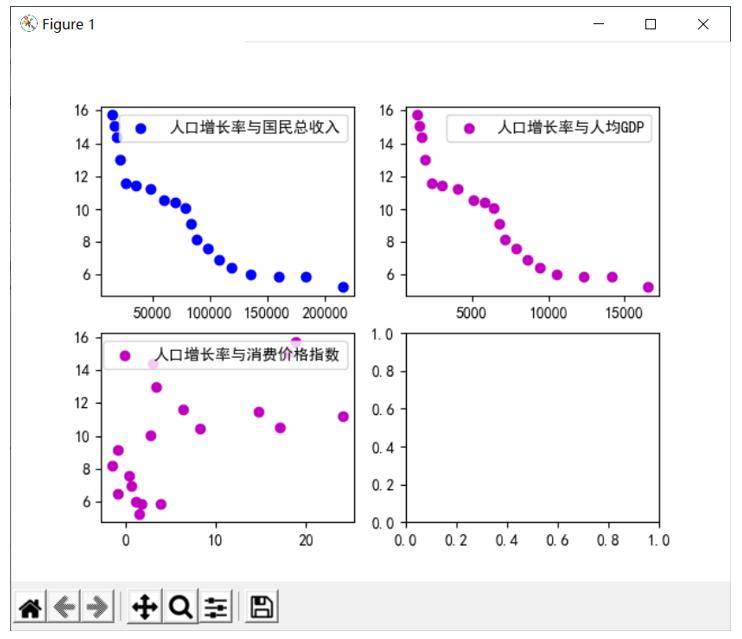
从散点图可以看出，人口增长率与国民总收入、人均GDP呈现较好的线性关系，人口增长率与消费价格指数线性关系较弱，在本案例中，可以认为它们具有一定的线性关系。

由此，人口增长率与国民总收入、人均GDP、消费价格指数的线性关系可以假设用下面的多元线性回归模型来表示：

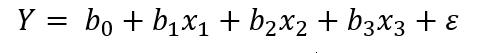
其中Y是人口增长率，b(0)、b(1)、b(2)是与x(1)、x(2)、x(3)无关的未知参数（也称为系数或权重），x(1)是国民总收入，x(2)是人均GDP，x(3)是消费价格指数，ε是预测值与Y的误差。

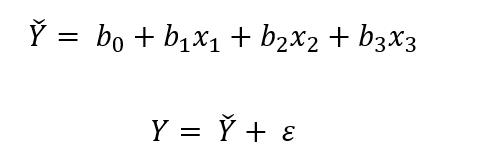
现在需要估计参数b(0)、b(1)、b(2)的值，设：

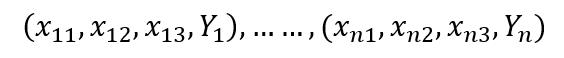
训练数据集的样本，和一元线性回归的情况一样，我们用最小二乘法来估计参数，即：

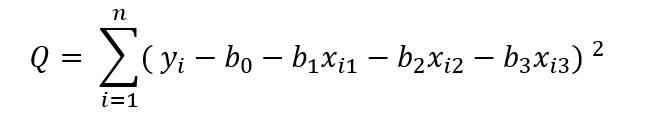
达到最小。

要使Q的值最小，用微积分的方法分别求Q分别关于b(0)、b(1)和b(2)的偏导数，并令导数等于零，得到一组方程，然后解方程即求得b(0)、b(1)和b(2)的值。

在本案例中，我们使用矩阵来求b(0)、b(1)和b(2)的值，多元回归使用矩阵方法求解要比微积分方法简单的多。

设矩阵A为训练集自变量样本特征矩阵，向量X为自变量参数向量，向量Y为训练集因变量向量。

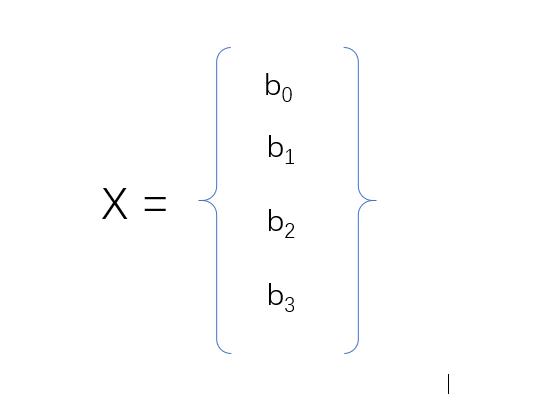
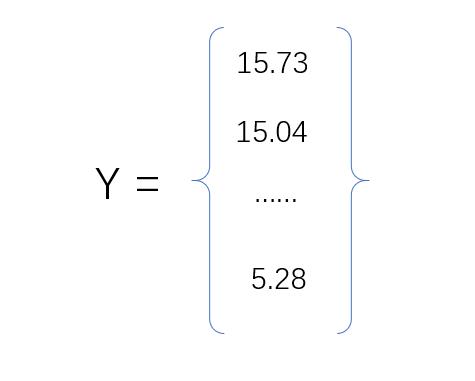
其中矩阵A第1列的值都为1，主要是方便矩阵A与向量X相乘运算。前面假设的多元线性回归模型可以使用下面的矩阵方程来描述：

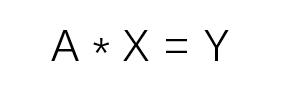
矩阵A乘以向量X，其结果是向量Y，但这个方程可能不成立，因为A乘以向量X的结果是预测值，预测值和真实值会存在误差，这个误差就是误差向量ε：

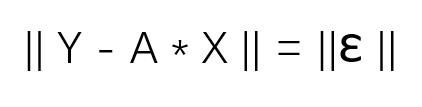
既然方程无解，只能求出最接近真实值的解。因为A*X的结果依然在矩阵A的列空间内，而Y不一定在A的列空间内，所以要微调Y，将Y变为A列空间内离Y最近的那个向量P：

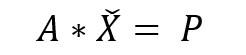
P是Y在A列空间内的投影，X顶部加个帽子符号，表示X和原来的X有所不同，它是最接近解的X。误差向量ε就是Y在A列空间内的投影P与Y向量的差。我们需要找到合适的向量X，让误差向量ε垂直于投影P。

我们知道曲线或直线外一点到该曲线或直线的垂直距离最短，即最接近Y的真实值。要让误差向量ε取值最小，就需要找到合适的向量X，满足向量ε垂直于矩阵A列空间内的向量，当然也垂直于投影P。

即：

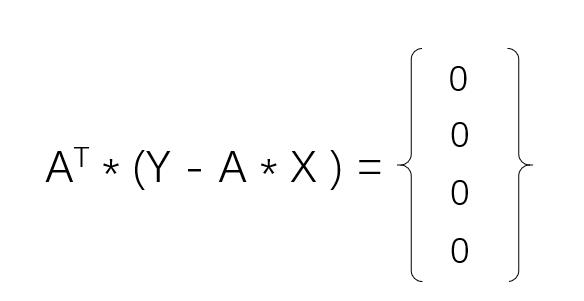
其中矩阵A、向量Y已知，上面的矩阵方程可以改写为：

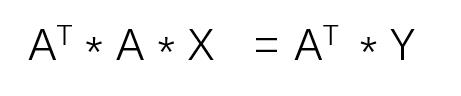
例2  求解向量X

# 导入numpy库
import numpy as np
  
# 创建矩阵A
def matrix_a(data):
    alist = list(data[::,2:5])
    newlist = []
    # 矩阵A添加1列，数值为1
    for item in alist:
        temp = list(item)
        temp.insert(0,1)
        newlist.append(temp)
    return np.array(newlist)
  
# 创建向量Y
def matrix_y(data):
    ylist = data[::,1:2]
    return np.array(ylist)
  
# 程序入口
if __name__ == '__main__':
  
   # 读取训练集
   data = np.genfromtxt('train_population.csv',delimiter=',',dtype='float')
  
   # 创建矩阵A
   A = matrix_a(data)
  
   # 创建向量Y
   Y = matrix_y(data)
  
   # A转置
   AT = np.transpose(A)
  
   # 计算A转置乘A
   ATA = np.matmul(AT,A)
   # 计算A转置乘Y
   ATY = np.matmul(AT,Y)
   # 解向量X
   X = np.linalg.solve(ATA,ATY)
   print("b0:%f
b1:%f
b2:%f
b3:%f" % (X[0],X[1],X[2],X[3]))

执行程序，求得预测模型的参数为：

b0:15.880460
b1:0.000596
b2:-0.008440
b3:0.072519

多元回归输出预测模型为：

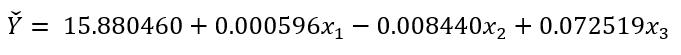
模型性能度量

对模型的性能度量，主要采用绘图直观比较和均方误差进行。性能度量使用的数据集为test_population.csv，该数据集存储了2009年、2010年、2011年国民人口增长率的数据。

例3  绘图直观比较

# 导入numpy库
import numpy as np
import matplotlib.pyplot as plt
  
# 定义参数
b0 = 15.880460
b1 = 0.000596
b2 = 0.008440
b3 = 0.072519
  
# 定义绘图函数
def plotter(ax, data1, data2, param_dict,type):
    if type == 0:
       ax.scatter(data1,data2,**param_dict)
    else:
       ax.plot(data1, data2, **param_dict)
   
# 测试集预测人口增长率
def test_forecast(data):
    x = np.arange(3)
    y = []
    for item in data:
        y.append(b0 + item[2]* b1 - item[3]* b2 + item[4]* b3)
    return (x,y)
  
# 训练集预测人口增长率
def train_forecast(data):
    x = np.arange(len(data))
    y = []
    for item in data:
        y.append(b0 + item[2]* b1 - item[3]* b2 + item[4]* b3)
    return (x,y)
  
# 获取X轴刻度标签
def get_labels(data):
    labels = []
    for item in data:
        labels.append(str(int(item)))
    return labels
  
# 定义计算MSE的函数
def calculation_mse(data,m):
    exp = ""
    for i,item in enumerate(data):
       format_str = "({0}-({1} + {2}* {3} - {4}* {5} + {6}*{7}))**2"
       sub_exp = format_str.format(item[1],b0,item[2],b1,item[3],b2,item[4],b3)
       exp += sub_exp
       if i != len(data) - 1:
           exp += "+"
    mse = eval(exp) / m
    return mse
  
  
# 程序入口
if __name__ == '__main__':
  
   # 设置图例中文显示
   plt.rcParams['font.sans-serif'] = ['SimHei']
  
   # 读取测试集
   test_data = np.genfromtxt('test_population.csv',delimiter=',',dtype='float')
   # 读取训练集
   train_data = np.genfromtxt('train_population.csv',delimiter=',',dtype='float')
   # 获取测试集人口实际增长率
   test_y = test_data[::,1]
   test_x = np.arange(len(test_data))
   # 获取训练集人口实际增长率
   train_y = train_data[::,1]
   train_x = np.arange(len(train_data))
  
   # 创建子图
   fig, ax = plt.subplots(1,2)
  
   ax[0].set_title('测试集')
   test_labels = get_labels(test_data[::,0])
   # 设置测试集子图X轴刻度显示格式
   ax[0].set_xticks(test_x)
   ax[0].set_xticklabels(test_labels)
   # 绘制测试集人口增长率真实值
   plotter(ax[0],test_x,test_y,{'color': 'm','label':'真实人口增长率'},0)
   # 获取测试集人口增长率预测值
   testx,testy = test_forecast(test_data)
   # 绘制测试集人口增长率预测值
   plotter(ax[0],testx,testy,{'color': 'b','label':'预测人口增长率'},0)
   ax[0].legend()
  
   ax[1].set_title('训练集')
   ax[1].set_xticks(train_x)
   train_labels = get_labels(train_data[::,0])
   ax[1].set_xticklabels(train_labels)
   # X轴刻度值旋转70度
   plt.setp(ax[1].xaxis.get_majorticklabels(), rotation=70)
   # 绘制训练集人口增长率真实值
   plotter(ax[1],train_x,train_y,{'color': 'm','label':'真实人口增长率'},0)
   # 获取训练集人口增长率预测值
   trainx,trainy = train_forecast(train_data)
   # 绘制测试集人口增长率预测值
   plotter(ax[1],trainx,trainy,{'color': 'b','label':'预测人口增长率'},0)
   ax[1].legend()
   
  
   # 计算测试集MSE
   test_mse = calculation_mse(test_data,len(test_data))
   mse = "MSE=" + str(test_mse)
   ax[0].text(0.1,1.0,mse,color='r')
   
   # 计算训练集MSE
   train_mse = calculation_mse(train_data,len(train_data))
   mse = "MSE=" + str(train_mse)
   ax[1].text(1,4.5,mse,color='r')
   plt.show()

性能度量效果如下图所示：

上面的程序代码是模型的性能度量P，从散点图和均方误差（MSE）看，训练数据的拟合度较好，均方误差约为0.91，测试集的拟合度较差，均方误差为7.40，测试集的均方误差远大于训练集的均方误差，这种现象属于过拟合。

产生过拟合的现象有多种因素，如训练集的样本过少、特征数据的噪声（外部环境可能会影响到特征数据的变化）等都会产生过拟合现象，后面课程讲述的参数正则化可以减少过拟合现象的发生，当然也要增大训练集的样本数量。

文中案例代码和数据集可在编程训练营APP下载。

— END—

编程训练营APP

创新在线学习模式，学习编程不再半途而废

安卓手机应用商店

搜索编程训练营下载