B+树-查找插入与删除

Posted 2021-10-06 都璐璐

写15645的作业卡在B+树上了，写一篇文章梳理一下基本的知识点。大部分参考课件与Database System Concepts (7th Edition)。

B+ 树

for a n-way B+-tree:
A B+-tree index takes the form of a balanced tree in which every path from the root of the tree to a leaf of the tree is of the same length.
Each nonleaf node in the tree (other than the root) has between ⌈n∕2⌉ and n children, where n is fixed for a particular tree; the root has between 2 and n children.
Each leaf can hold up to n − 1values. We allow leaf nodes to contain as few as ⌈(n − 1)∕2⌉ values.
B+树的定义有多个版本，有些可能会使用keys（values）而不是children来定义nonleaf node。在这种情况下，只需要记住inner node with k keys has k+1 non-null children即可以进行转换。比如has between ⌈n∕2⌉ and n children，对应的就是⌈n∕2⌉ - 1 and n - 1 keys。

B+树的查找

查找主要分为两类：单值查找与范围查找(range queries)。
以下给出两种操作的伪代码，要理解这个伪代码，首先要理解B+树结点的基本结构。对于某个key， Ki，左右各有一个结点，左节点Pi指向的孩子节点值均小于Ki，右结点Pi+1，指向的孩子结点值>=Ki。

单值查找的伪代码：
单值查找其实是从root到leaf的遍历过程。过程主要是查找到对应的可能的leaf，判断是否存在，若不存在返回Null。时间复杂度不会超过⌈log⌈n∕2⌉（N）⌉，N代表记录数。这个时间复杂度可以这么理解，当每个结点的children越少，层数可能越高，B+树的要求最少为⌈n∕2⌉个children。

范围查找的伪代码：

范围查找的主要过程是查找到最小值对应的key，然后沿着leaf结点之间的指针向后遍历直至终点。时间复杂度包括，单值查找最小值的复杂度和顺序遍历的复杂度。 顺序遍历的复杂度可以这样计算，如果会连续遍历M个指针（每个值会对应于一个指针），每个leaf nodes最少有⌈n ∕2⌉个指针，最多就会遍历⌈M ∕(n / 2)⌉+1个叶子结点。如果是secondary index的话，由于记录可能分布在不同的块上，最差可能会导致M次随机I/O操作。如果是clustered index，因为记录存储在连续的块上，能最大程度降低消耗。

B+树的更新

可以主要分为插入和删除两类。因为对一个key的更新可以分解为，先删除原有的key然后再插入新的key，所以update操作在这里不予考虑。 插入和删除，在查找目标值的基础上，还增加了结构调整的操作，相对来说较为复杂。插入操作的结构调整，主要是页分裂。删除操作的结构调整，相对于插入更加复杂一些，主要是页合并（coalesce）和重分配（redistribute）。

更新

更新的伪代码。代码中的pointer的意义：Instead, an entry (Gold, n2) is added to the parent node, where n2 is a pointer to the newly created node that resulted from the split.基本的过程就是判断，需要插入到的结点目前是否已经满了（已有n-1个值），如果满了要进行页分裂操作（创建一块新的内存，把原来页的值拷贝过去，在适宜的位置插入新的值，然后一半分给L结点，一半分给L\'结点），然后递归操作父节点。

因为不是很难所以这里先不叙述具体过程了。可以看两个书里面具体的插入示例，结合伪代码理解以下各个分支的过程与导致的结果。

示例一：
原始：

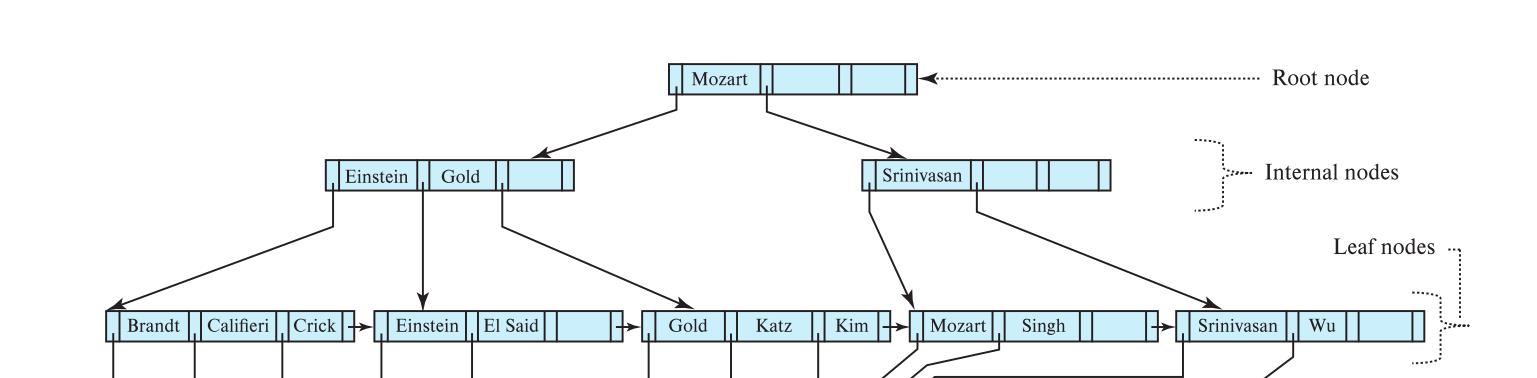
插入Adams，可以看到递归过程把Califieri插入到了父节点。

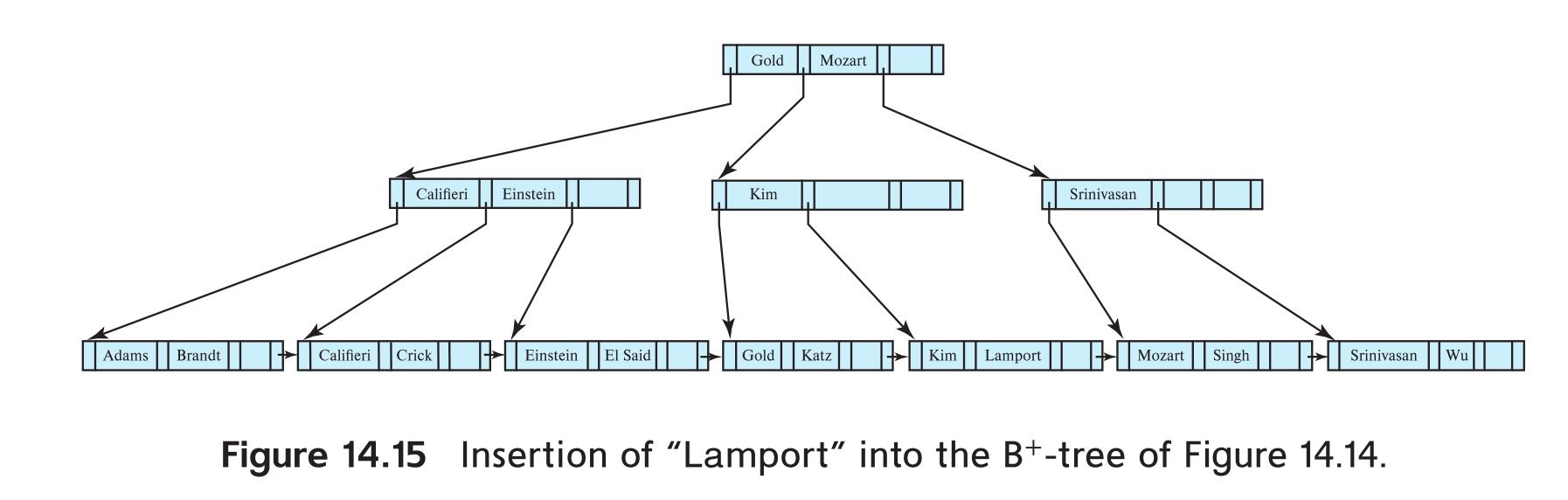
示例二：
以刚刚的结果为起点，插入“Lamport”。
结果：（因为父节点的兄弟结点满了，再次触发页分裂操作，所以一直递归到了根节点）

删除

删除的伪代码如下，先不要细看，因为乍一看比较复杂。原书说明了这个P指针到底是什么，当是叶子结点的时候P是它前一个指针，否则是跟着K值的后一个指针：The pseudocode refers to deleting an entry (K, P) from a node. In the case of leaf nodes, the pointer to an entry actually precedes the key value, so the pointer P precedes the key value K. For nonleaf nodes, P follows the key value K.

接下来用三个书上的示例来说明以下这段代码。

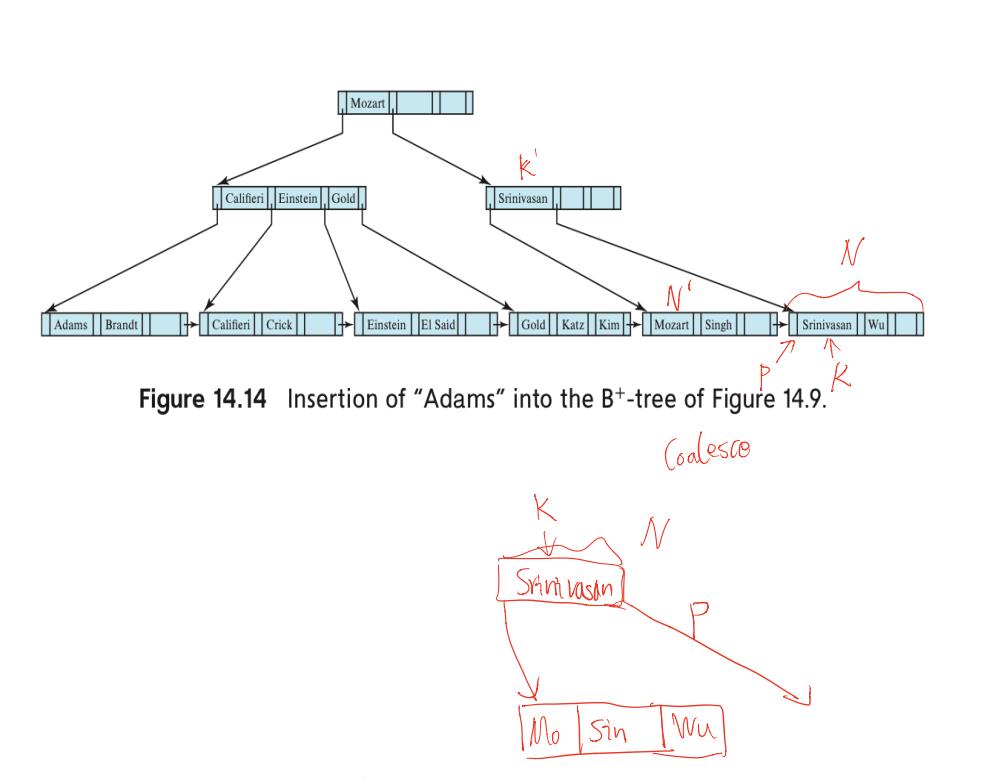
示例1. 原始情况，要删除“Srinivasan”这个值

第一步，通过遍历查找到“Srinivasan”这个值， K为该值，P为前一个指针，N为K所在的结点，进入到delete entry这个函数。先删除K、P，N不是root且N结点由于只剩下一个值“Wu”，不符合叶子节点至少要有⌈(n − 1)∕2⌉ values的条件（n为4，叶子结点至少要有2个值），N\'为兄弟节点，K\'为父结点的值（被N和N\'夹着的父节点的值）。判断N和N\'能不能放在一个结点，结果是可以，N\'只有2个值，N剩下1个值，叶子结点最多可以放下n-1个值（也就是3），因此触发coalesce合并。将N的所有值加入到N\'结点中。结果如下图。然后递归操作，delete entry(node N, value K, pointer P)，新的N为原始N的父节点，新K为父节点的值，P为父节点与原始N之间的指针。

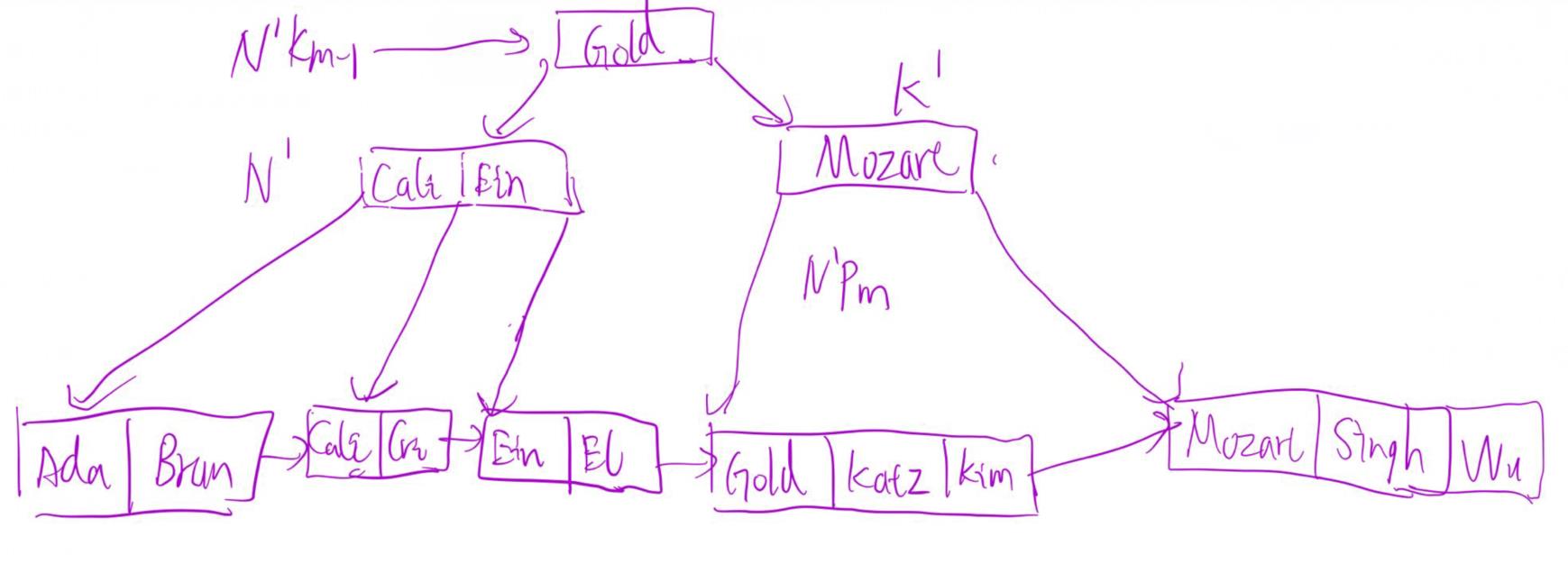
新的K、N、P、K\'、N\'如图所示。先删除（K,P），N不是根节点。判断N和N\'能不能放在一个结点。结果是不能，因为兄弟结点N\'满了（有4个孩子），所以触发redistribute操作。这一步操作用语言来描述就是（要求N\'为前置结点，否则需要对称操作），找到N\'的最后一个值（N\'Km-1）与指针（N\'Pm），从N\'中删掉两者。父节点的值（K\'）下移，左指针变为N\'最后一个指针（N\'Pm），右边连接N的所有值与指针。N\'的最后一个值（N\'Km-1），变为父节点的值。过程如下图所示。

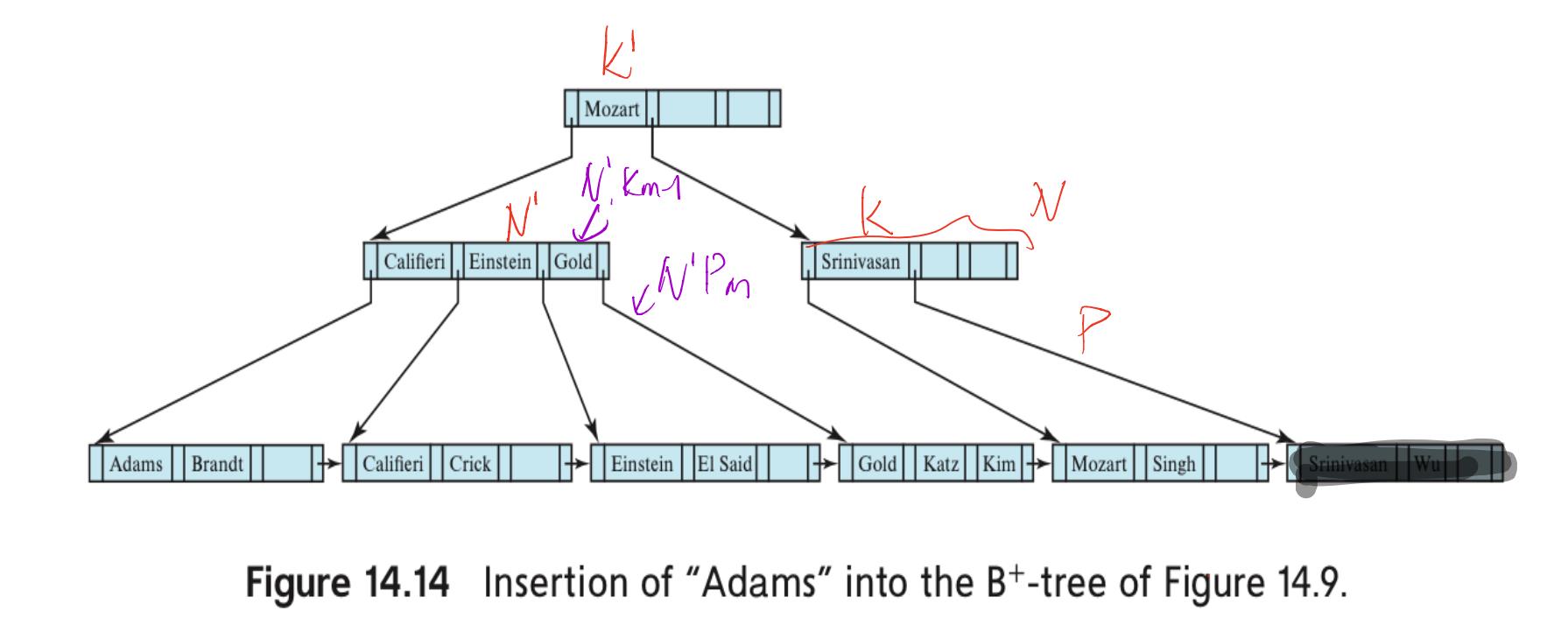
整个过程结束，得到最终结果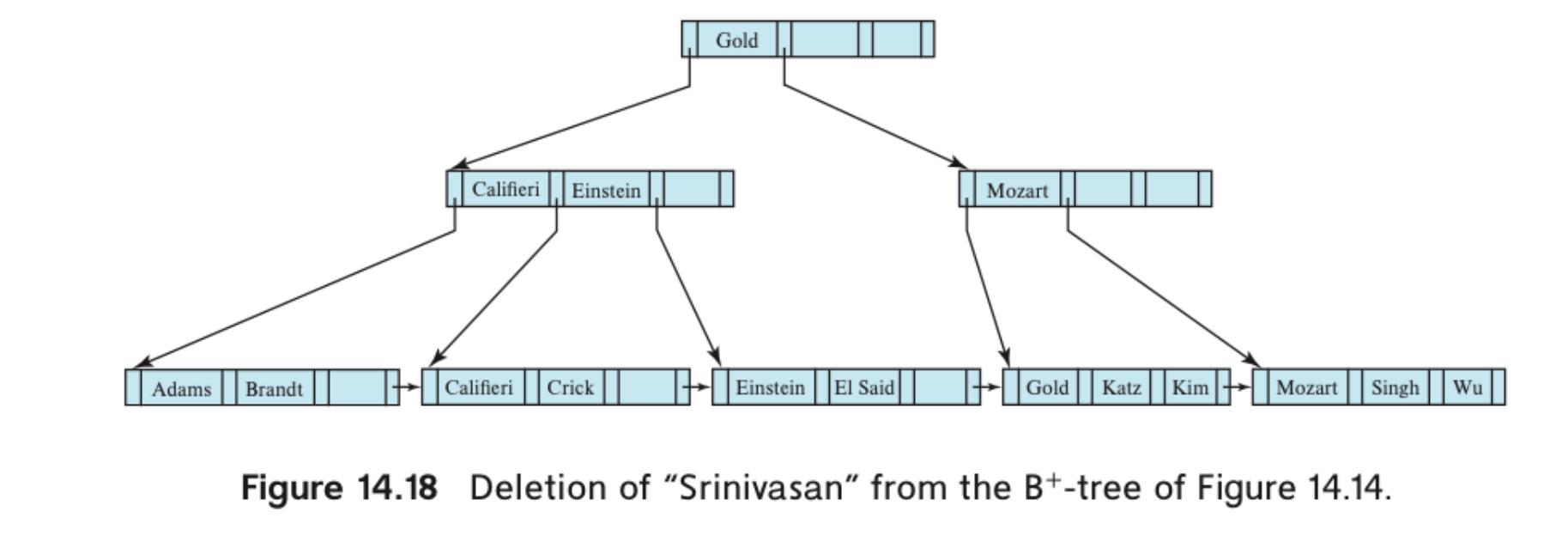

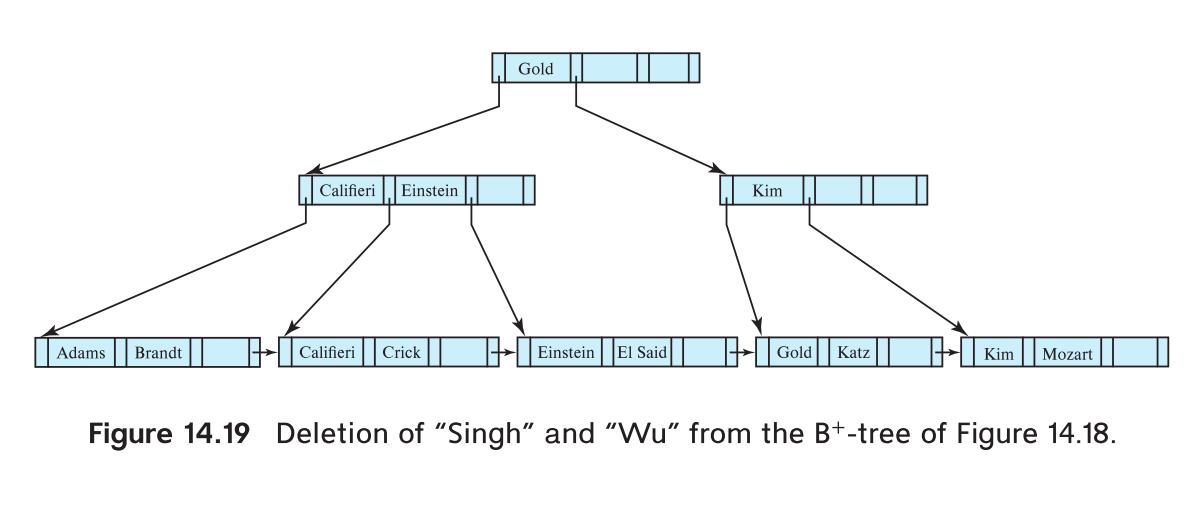
示例2. 原始情况就是刚刚得到的结果，要删除“Singh”和“Wu”这2个值。这个过程较为简单，删掉2个值之后，结点只剩下1个值了不符合叶子结点至少要有2个值的条件，而兄弟结点满了，所以触发redistribute。因为N是叶子结点，它的redistribute和刚刚的redistribute有些不同，走的是下面的这个分支。这个分支的主要操作是，找到N\'的最后一个结点和值，从N\'中删掉他们，然后插入到N结点的左边，然后父节点的值替换为N\'的最后一个值。

结果如下所示：

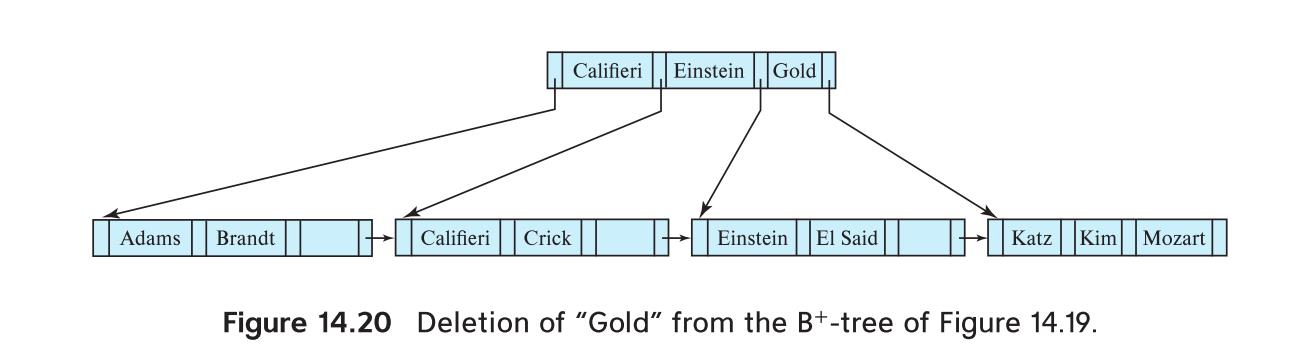
示例3. 原始情况就是刚刚得到的结果，要删除“Gold”这个值。首先要查找到叶子结点，找到Gold所在的位置，把它删掉。会导致“Gold”所在结点只剩下一个值不符合叶子结点至少要有2个值的条件，而兄弟结点（有同一个父节点的才叫兄弟结点）没有满，因此可以合并两个结点。这个时候父节点只有一个子节点了，不符合中间结点至少要有⌈n∕2⌉个孩子的条件，父节点的兄弟结点这个时候没有满，因此再次触发合并操作，这个合并操作也和刚刚的有少许不同。先删掉“Kim”结点和指针，由于N不是叶子结点，所以把父节点的值！和其他N的值与结点加入到N’中。

然后继续递归，这个时候由于N已经是根节点了，而且只有一个子结点，删掉自己，把孩子结点作为根节点即可。

结果如下，删除操作导致层高降低了：