B树的相关概念及其插入删除操作（C语言）

Posted 2021-09-04 bfhonor

一、B树

（一）5叉查找树

//5叉排序树的结点定义
struct Node{
	ElemType keys[4];	//最多4个关键字
	struct Node * child[5];//最多5个孩子
	int num;	//结点中有几个关键字
};

（二）如何查找

• 查找元素9。
  
  
• 查找目标：41。
  
  

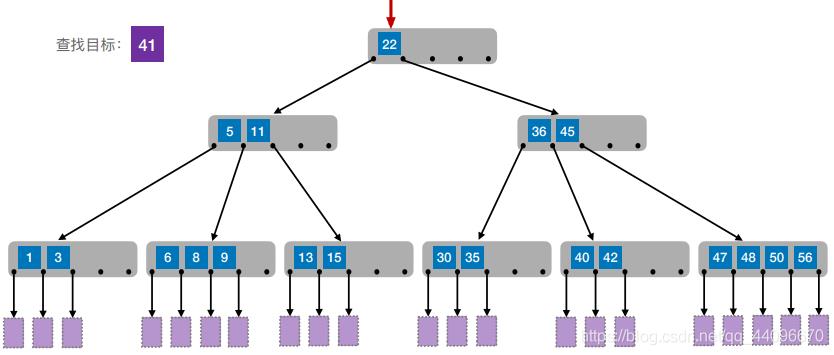
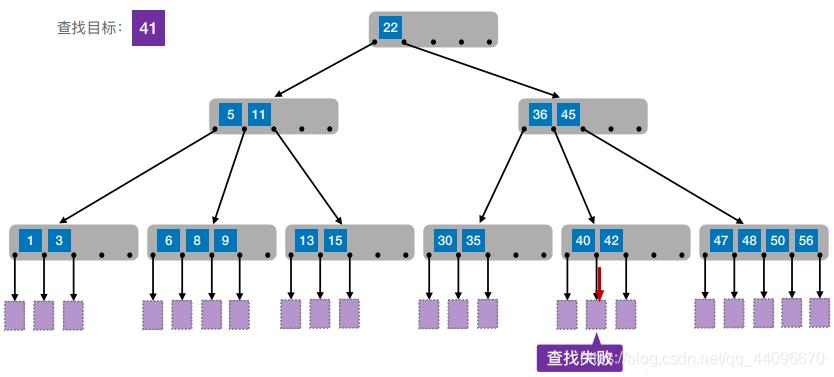
（三）如何保证查找效率

• eg：对于5叉排序树，规定除了根节点外，任何结点都至少有3个分叉，2个关键字
• 若每个结点内关键字太少，导致树变高，要查更多层结点，效率低
  
  
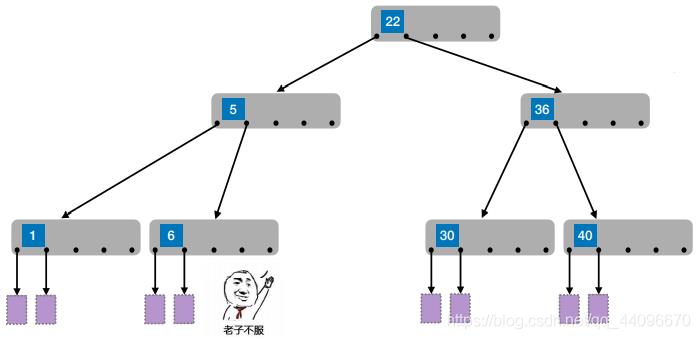
• 策略1：m叉查找树中，规定除了根节点外，任何结点⾄少有⌈m/2⌉个分叉，即至少含有⌈m/2⌉ − 1 个关键字
  
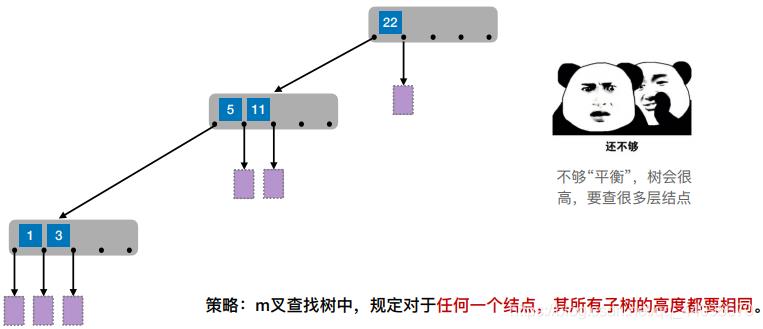
• 策略2：m叉查找树中，规定对于任何一个结点，其所有子树的高度都要相同。
• 对于同时满足策略1和策略2的树，称其为B树。

（四）B树

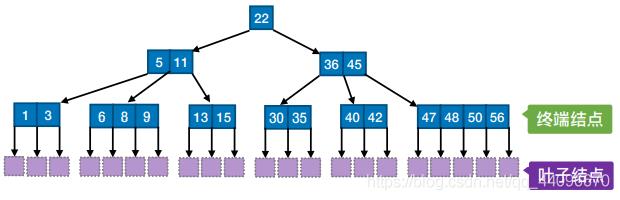
• B树，又称多路平衡查找树，B树中所有结点的孩子个数的最大值称为B树的阶，通常用m表示。一棵m阶B树或为空树，或为满足如下特性的m叉树：
  ①、树中每个结点至多有m棵子树，即至多含有m-1个关键字。
  ②、若根结点不是终端结点，则至少有两棵⼦树。
  ③、除根结点外的所有非叶结点至少有⌈m/2⌉棵子树，即至少含有 ⌈m/2⌉ − 1个关键字。
  ④、所有的叶结点都出现在同⼀层次上，并且不带信息（可以视为外部结点或类似于折半查找判定树的查找失败结点，实际上这些结点不存在，指向这些结点的指针为空）。
  

1. m阶B树的核心特性：

• （1） 根节点的⼦树数∈[2, m]，关键字数∈[1, m-1]。
  其他结点的⼦树数∈[ ⌈m/2⌉ , m]；关键字数∈[ ⌈m/2⌉ -1, m-1]
• （2）对任⼀结点，其所有⼦树⾼度都相同
• （3）关键字的值：子树0<关键字1<⼦树1<关键字2<⼦树2<…. (类⽐⼆叉查找树 左<中<右)

2. B树的高度

• 注：大部分学校算B树的高度不包括叶子结点（失败结点）
• 问题：含n个关键字的m阶B树，最小⾼度、最大⾼度是多少？
  
  
  

二、B树的插入和删除

（一）B树的插入

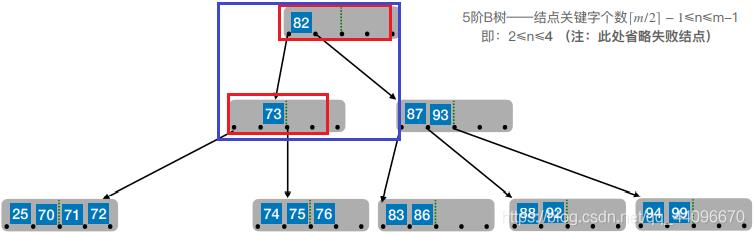
• 5阶B树——结点关键字个数 ⌈m/2⌉ − 1≤n≤m-1即：2≤n≤4 （注：此处省略失败结点）
  
  
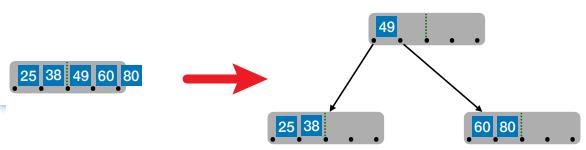
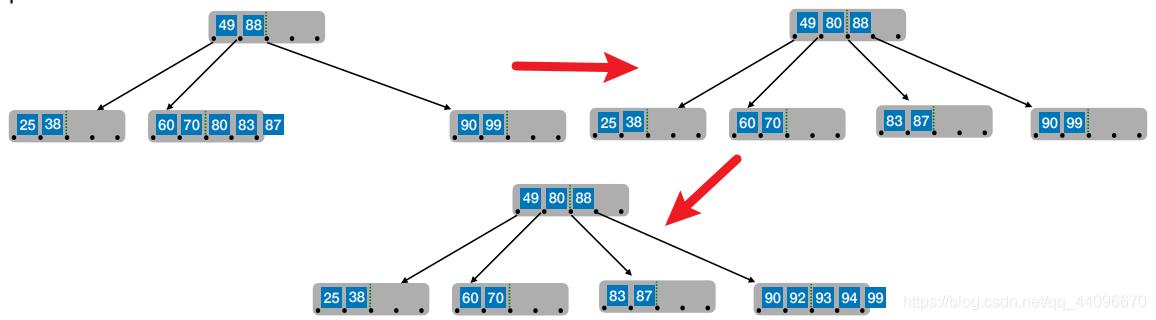
• 在插入key后，若导致原结点关键字数超过上限，则从中间位置（⌈m/2⌉）将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置（⌈m/2⌉）的结点插⼊原结点的父结点
• 新元素一定是插入到最底层“终端节点”，用“查找”来确定插入位置
  
  
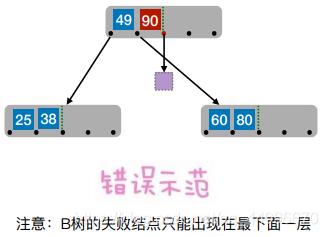
• 在插入key后，若导致原结点关键字数超过上限，则从中间位置（⌈m/2⌉）将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置（⌈m/2⌉）的结点插⼊原结点的父结点
  
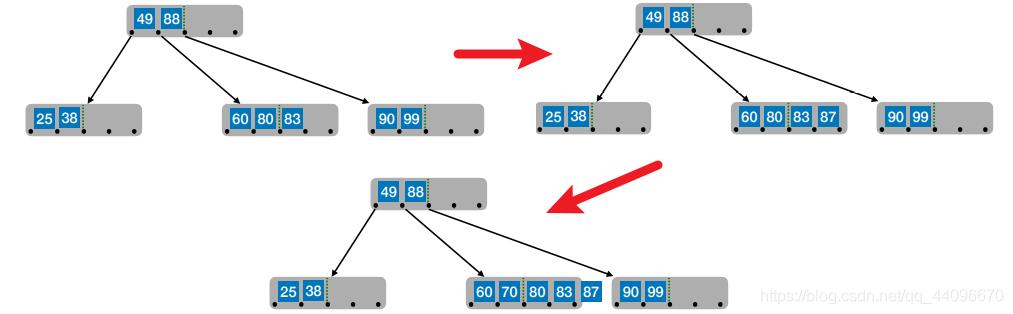
• 思考：80要放到父节点中，放在哪个位置合适？
  
  
  
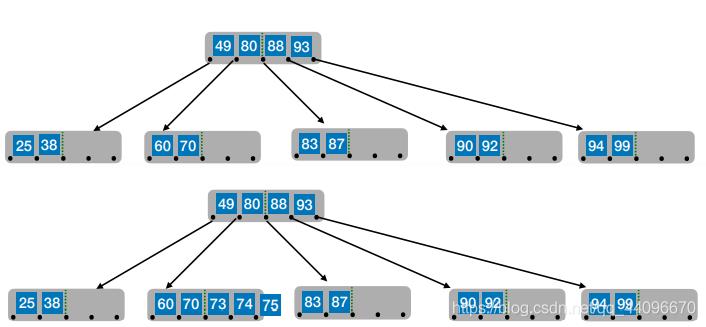
• 在插入key后，若导致原结点关键字数超过上限，则从中间位置（⌈m/2⌉）将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置（⌈m/2⌉）的结点插入原结点的父结点。若此时导致其⽗结点的关键字个数也超过了上限，则继续进⾏这种分裂操作，直至这个过程传到根结点为止，进而导致B树高度增1。
  

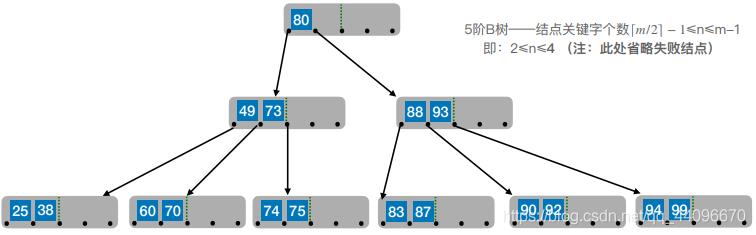
（二）B树的删除

1. 删除目标结点：60

• **若被删除关键字在非终端节点，则⽤直接前驱或直接后继来替代被删除的关键字

2. 删除目标结点：80

• 直接前驱：当前关键字左侧指针所指子树中“最右下”的元素**
  

3. 删除目标结点：77

• 直接后继：当前关键字右侧指针所指子树中“最左下”的元素
  
  
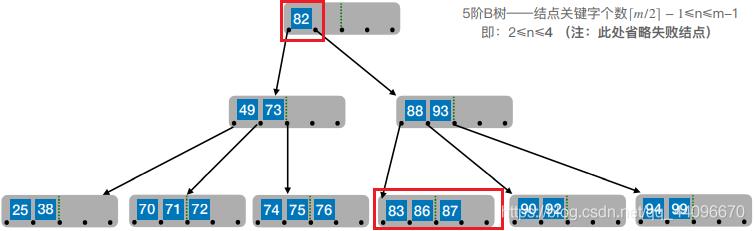
• 对非终端结点关键字的删除，必然可以转化为对终端结点的删除操作

4. 删除目标结点：38

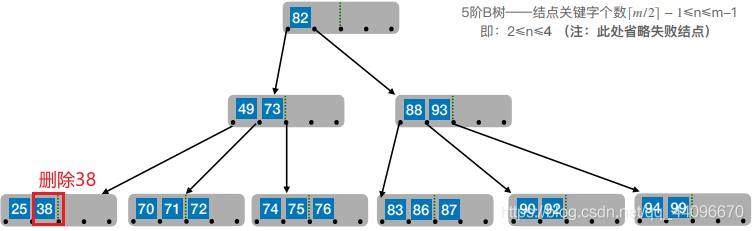
• 兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限，且与此结点右（或左）兄弟结点的关键字个数还很宽裕，则需要调整该结点、右（或左）兄弟结点及其双亲结点（父子换位法）
  
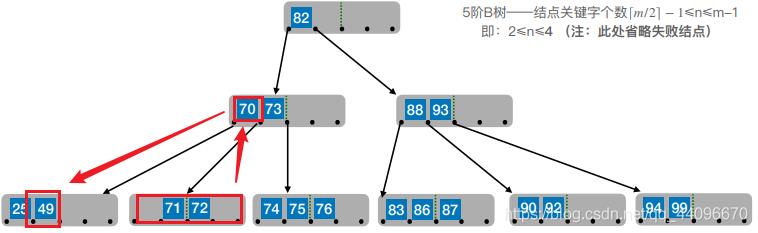
• 说白了，当右兄弟很宽裕时，用当前结点的后继、后继的后继 来填补空缺

5. 删除目标结点：90.

• 当左兄弟很宽裕时，用当前结点的前驱、前驱的前驱 来填补空缺
• 本质：要永远保证子树0<关键字1<⼦树1<关键字2<⼦树2<….

6. 删除目标结点：49

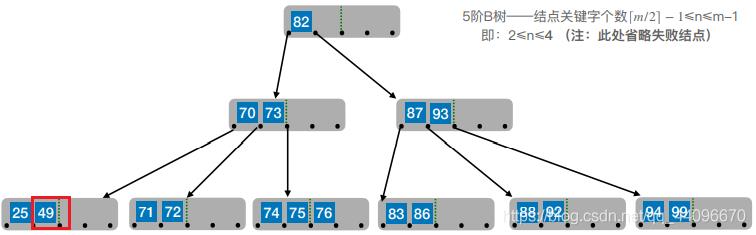
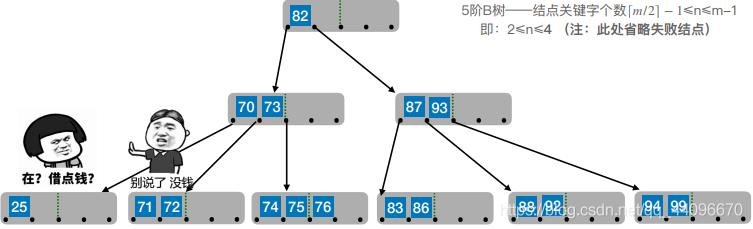
• 兄弟不够借。若被删除关键字所在结点删除前的关键字个数低于下限，且此时与该结点相邻的左、右兄弟结点的关键字个数均=⌈m/2⌉ − 1，则将关键字删除后与左（或右）兄弟结点及双亲结点中的关键字进⾏合并
  
  
  
  
• 在合并过程中，双亲结点中的关键字个数会减1。若其双亲结点是根结点且关键字个数减少至0（根结点关键字个数为1时，有2棵子树），则直接将根结点删除，合并后的新结点成为根；若双亲结点不是根结点，且关键字个数减少到 ，则又要与它自己的兄弟结点进行调整或合并操作，并重复上述步骤，直至符合B树的要求为止。