树链剖分入门

Posted 2021-08-26 conprour

前言

借鉴题解树链剖分详解（洛谷模板 P3384） - ChinHhh - 博客园 (cnblogs.com)

一直觉得树链剖分是一个挺高级的东西（想象把一棵树分解的美妙过程...），实际上思路不是特别难理解，就是细节的地方想要全都理解透彻也需要点耐心

题解

树链剖分 就是对一棵树分成几条链，把树形变为线性，减少处理难度

需要处理的问题：

• 将树从x到y结点最短路径上所有节点的值都加上z
• 求树从x到y结点最短路径上所有节点的值之和
• 将以x为根节点的子树内所有节点值都加上z
• 求以x为根节点的子树内所有节点值之和

其实只有前两个问题算树剖，下面两个问题线段树＋普通dfs序就可以解决

概念

• 重儿子：对于每一个非叶子节点，它的儿子中 儿子数量最多的那一个儿子 为该节点的重儿子
• 轻儿子：对于每一个非叶子节点，它的儿子中 非重儿子 的剩下所有儿子即为轻儿子
• 叶子节点没有重儿子也没有轻儿子（因为它没有儿子。。）
• 重边：连接任意两个重儿子的边叫做重边
• 轻边：剩下的即为轻边
• 重链：相邻重边连起来的 连接一条重儿子 的链叫重链
• 对于叶子节点，若其为轻儿子，则有一条以自己为起点的长度为1的链
• 每一条重链以轻儿子为起点

这个图不错，很有助于理解基础概念

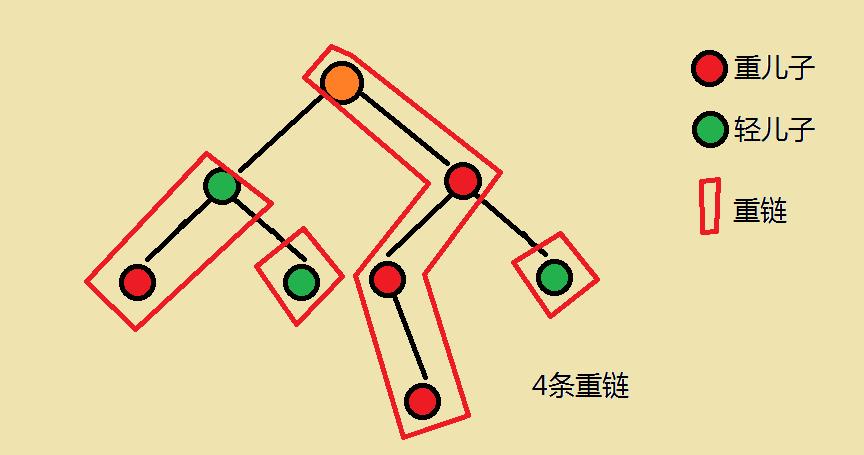
整体思路

• 用一个 dfs1 求出重儿子（这是主要任务）和相关信息，这一步没有难度（看代码也知道）
• 用一个 dfs2 从根往下搜索，边走边记录dfs序（这是主要任务），先走重儿子直到叶子节点，回溯再走轻儿子，这是为让所有重链都形成连续编号的区间
• 把树上的点维护成序列，查改用线段树
• 改两点路径上的点，用树链剖分求LCA的类似思路往上跳，跳到两个点在同一个重链为止，过程中得到线段树中要查询／修改的区间

一些细节的理解

• 这里的重链都以一个轻儿子为顶端（也就是起点）
• 线段树上修改/查询的时候实际上只对重链操作（因为所有点一定都在某一条重链上），和轻链没有关系，再计算轻链上的点会重复

代码注释的地方都是我思考过的地方，还是挺详细的

代码

树链剖分模板

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ls k<<1
#define rs k<<1|1
const int INF = 0x3f3f3f3f,N = 2e5+10;
int n,m,r,mod;
struct Edge{int to,nxt;}a[N<<1];
int head[N<<1],ecnt = -1;
inline void add(int u,int v){
	a[++ecnt] = (Edge){v,head[u]};
	head[u] = ecnt;
}
int siz[N],hson[N],dep[N],f[N],id[N],w[N],pos[N],top[N];
int cnt;
void dfs1(int u,int fa)//找出重儿子，预处理出f，dep，siz数组 
{
	siz[u]=1;
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(v==fa) continue;
		f[v]=u;
		dep[v]=dep[u]+1;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>siz[hson[u]]) hson[u]=v;
	}
}
void dfs2(int u,int tp)
{
	id[u]=++cnt,pos[cnt]=u;//id实际上是新的dfn，pos记录新点原来的编号 
	top[u]=tp;//记录链的顶端，每一条重链以轻儿子为起点 
	if(hson[u]) dfs2(hson[u],tp);//先走重儿子 
	for(int i=head[u];~i;i=a[i].nxt)//再走轻儿子 
	{
		int v=a[i].to;
		if(v==f[u]||v==hson[u]) continue;
		dfs2(v,v);//轻儿子的顶端是自己 
	}
}
//和普通的线段树区间修改+区间查询完全一致 
int tree[N<<2],lazy[N<<2];
void build(int k,int l,int r){
	if(l == r){tree[k] = w[pos[l]]%mod; return;}//只有这里和普通线段树有点不一样了 
	int mid = (l + r) >> 1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	tree[k] = (tree[k<<1] + tree[k<<1|1]) % mod;
}
inline void Add(int k,int l,int r,int v){
	(lazy[k] += v) %= mod;
	(tree[k] += (r-l+1)*v) %= mod;
}
inline void pushdown(int k,int l,int r){
	if(!lazy[k])return;
	int mid = (l + r) >> 1;
	Add(k<<1,l,mid,lazy[k]);
	Add(k<<1|1,mid+1,r,lazy[k]);
	lazy[k] = 0;
}
void modify(int k,int l,int r,int x,int y,int v){
	if(x <= l && r <= y){Add(k,l,r,v);return;}
	pushdown(k,l,r);
	int mid = (l + r) >> 1;
	if(x <= mid) modify(k<<1,l,mid,x,y,v);
	if(y > mid)  modify(k<<1|1,mid+1,r,x,y,v);
	tree[k] = (tree[k<<1] + tree[k<<1|1]) % mod;
}
int query(int k,int l,int r,int x,int y){
	if(x <= l && r <= y)return tree[k];
	pushdown(k,l,r);
	int mid = (l + r) >> 1 , ret = 0;
	if(x <= mid) (ret += query(k<<1,l,mid,x,y)) %= mod;
	if(y > mid)  (ret += query(k<<1|1,mid+1,r,x,y)) %= mod;
	return ret;
}
void change(int x,int y,int v)
{
	while(top[x]!=top[y])//当x，y不在同一条重链中 
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);//和83行对应，跳x，y中对应链顶端较深的那个点 
		modify(1,1,n,id[top[x]],id[x],v);
		x=f[top[x]];//【第83行】跳到这条重链顶端的父亲 
	}
	//if(dep[x]>dep[y]) swap(x,y);
	if(id[x]>id[y]) swap(x,y);//最后把x，y的路径修改好,由于这时x，y在同一条重链中，所以也可以写成上一行那样 
	modify(1,1,n,id[x],id[y],v);
}
int Query(int x,int y)//思路和change函数基本一样 
{
	int res=0;
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		res+=query(1,1,n,id[top[x]],id[x]);
		res%=mod;
		x=f[top[x]];
	}
	//if(dep[x]>dep[y]) swap(x,y);
	if(id[x]>id[y]) swap(x,y);
	res+=query(1,1,n,id[x],id[y]);
	res%=mod;
	return res;
}
signed main()
{
	memset(head,-1,sizeof(head)); 
	scanf("%d%d%d%d",&n,&m,&r,&mod);
	for(int i=1;i<=n;i++) scanf("%d",&w[i]);
	for(int i=1;i<n;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v),add(v,u);
	}
	dfs1(r,-1);
	dfs2(r,r);//每一条重链以轻儿子为顶端 
	build(1,1,n);
	for(int i=1;i<=m;i++)	
	{
		int op,x,y,z;
		scanf("%d",&op);
		//这里是路径操作 
		if(op==1)
		{
			scanf("%d%d%d",&x,&y,&z);
			change(x,y,z);
		}
		if(op==2)
		{
			scanf("%d%d",&x,&y);
			printf("%d\\n",Query(x,y));
		}
		//这里是子树操作 
		if(op==3)
		{
			scanf("%d%d",&x,&z);
			modify(1,1,n,id[x],id[x]+siz[x]-1,z);
			/*这里我想了一下x和x的子树的新编号为什么是连续的
			虽然是先走重儿子再走轻儿子，但是可以想象子树里的点走完了才会回溯到上一层
			所以这么修改没错*/ 
		}
		if(op==4)
		{
			scanf("%d",&x);
			printf("%d\\n",query(1,1,n,id[x],id[x]+siz[x]-1)); 
			//同理这样查询肯定也没错 
		}
	}
	return 0;
}