高频面试考点--主要元素(用O(n)+O解决)
Posted C_YCBX Py_YYDS
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高频面试考点--主要元素(用O(n)+O解决)相关的知识,希望对你有一定的参考价值。
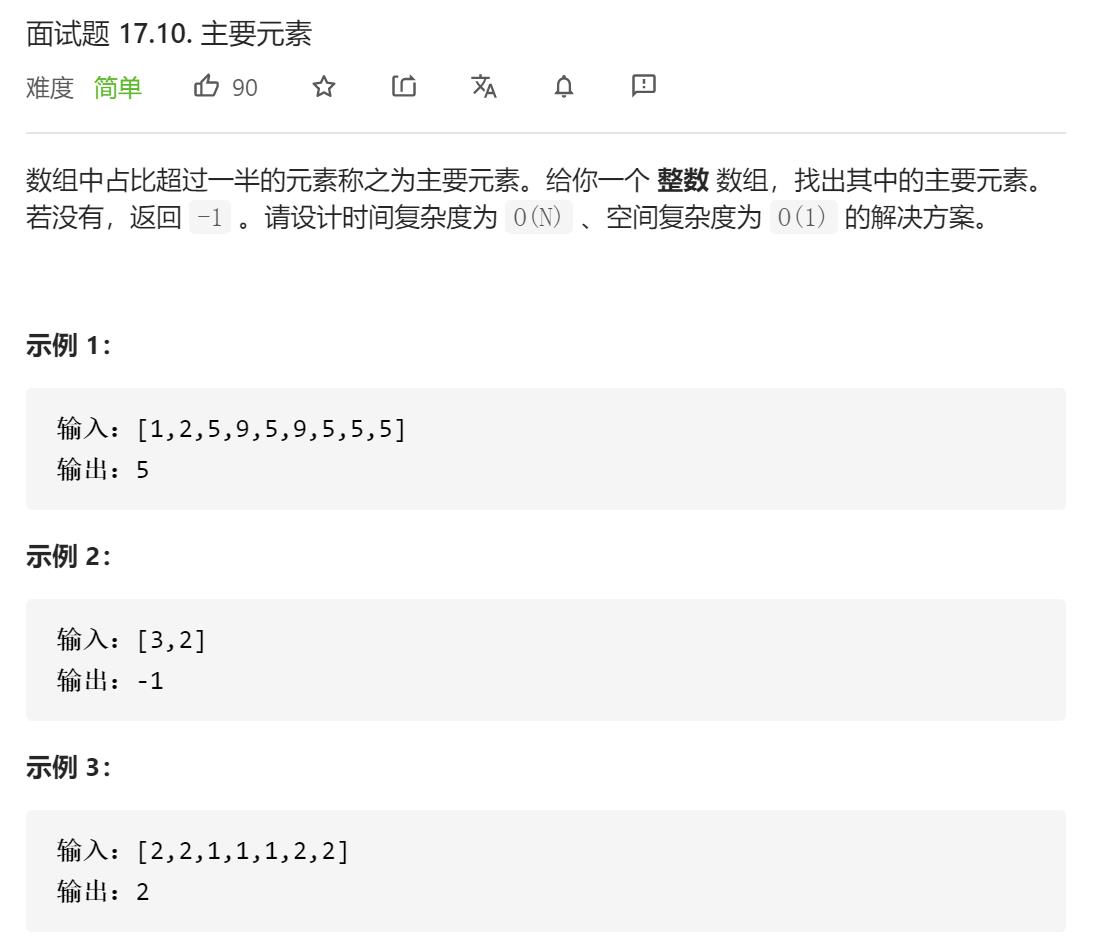
题目
题目解析
依据题意,主要元素一定是众数(因为主要元素出现次数一定大于数组的一半大小),但是众数不一定就是主要元素,所以我们的思路是先求出众数,再通过确定的众数扫描次数是否符合主要元素的情况。
关于寻找众数,一直有一个非常好的算法–摩尔投票法(能实现
时间复杂度O(n),空间复杂度O(1))
-
曾经在评论区看到过的形象描述:
摩尔投票法: -
核心就是对拼消耗。
玩一个诸侯争霸的游戏,假设你方人口超过总人口一半以上,并且能保证每个人口出去干仗都能一对一同归于尽。最后还有人活下来的国家就是胜利。
那就大混战呗,最差所有人都联合起来对付你(对应你每次选择作为计数器的数都是众数),或者其他国家也会相互攻击(会选择其他数作为计数器的数),但是只要你们不要内斗,最后肯定你赢。
最后能剩下的必定是自己人。
解题代码
效率还行
class Solution {
public:
int majorityElement(vector<int>& nums) {
int count = 1;
int res = nums[0];
int sz = nums.size();
//防止特殊情况i+1溢出,在后面加一个最后数字。
int a = nums.back();nums.push_back(a);
for(int i = 1;i<sz;i++){
//友军,增加兵力
if(res == nums[i])
count++;
else{//敌军,开始对拼消耗
count--;
//当敌军和友军正好同归于尽,则呼叫下一轮兵种
if(count==0)
res = nums[i+1];
}
}
//最终对拼得出的res就是众数,再来一层for循环寻找众数出现的次数,如果次数大于sz的一半便是主要元素
count = 0;
for(int i=0;i<sz;i++){
if(nums[i]==res)
count++;
}
return count>(sz/2)?res:-1;
}
};
以上是关于高频面试考点--主要元素(用O(n)+O解决)的主要内容,如果未能解决你的问题,请参考以下文章
