信息学赛培 | 09 总览全局的算法——广度优先搜索算法与实例详解

Posted 2021-07-24 AI与区块链技术

戳一戳！和我一起走进信息学的世界

导读

信息学能够有助于孩子未来工作发展，提升孩子的综合能力。

昨天我们学习了深度优先搜索算法，今天我们来看一下广度优先搜索算法算法，为什么老师会把广度优先搜索算法看作是总览全局的算法呢，广度优先搜索又有哪些趣味的案例呢？让我们走进本文看一下吧！

往期回顾

【NOIP竞赛/CSP认证】

▶  

▶  

▶  

【信息学精华帖】

▶  

▶  

▶  

▶  

▶  

【信息学集训】

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

【信息学集训】

▶  

▶   

▶   

▶   

▶   

▶   

▶   

▶   

▶   

▶   

▶  

▶  

▶  

▶  

▶  

▶  

【数据结构前导课】

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

【C++提高班教程】

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶   

▶   

▶   

【C++基础班教程】

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶  

▶    

1 深度优先搜索回顾

首先我们先来复习一下深度优先搜索。

深度优先搜索是不断往深入搜索，到达尽头返回上一层重新搜索，所以深度优先搜索需要两个过程：

搜索回溯

深度优先搜索思想如下：

搜索每一种情况如果不满足某些搜索条件，就跳出；如果满足某些搜索条件：1、搜索这种情况2、递归搜索和这种情况相关的其他情况3、回溯

两种比较常用的深度优先搜索结构如下：

int Search(int k){ for (i=1;i<=情况数;i++) if (满足条件){　　　　 保存结果　　　　 if (到目的地) 输出解;  else Search(k+1);　　　　     恢复：保存结果之前的状态　 　      }}

int Search(int k){　  if(到目的地) 输出解;　　　 else for(i=1;i<=情况数;i++)    if(满足条件){ 保存结果; Search(k+1); 恢复：保存结果之前的状态 }}

2 广度优先遍历

接下来我们来看一下广度优先遍历！

1 总览全局的视野

广度优先遍历不会“陷入”到某条路径中，每到一个顶点，就会总览全局，把所有相关的全部考虑到。然后再分别考虑进去。

广度优先遍历具有全局视野，深度优先遍历考虑局部视野。所以广度优先遍历更广，深度优先遍历更深。

2 广度优先遍历理论回顾

我们对于下图进行广度优先遍历：

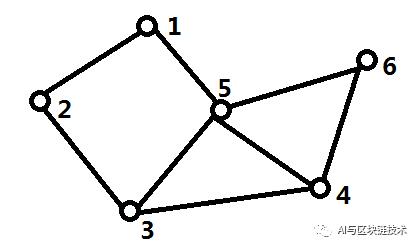
大家应该还记得，我们使用广度优先遍历的时候，要用到队列结构。

假如我们从1开始遍历，先让1入队，当前的队头是1，然后将1出队并把和1相邻的入队。队列元素如下：

25

当前的队头是2，然后将2出队并把和2相邻且没有访问过的入队。队列元素如下：

53

当前的队头是5，然后将5出队并把和5相邻的入队。队列元素如下：

346

一种停止的情况是当我们入队个数和顶点个数相同，那么我们就可以停止，然后出队到队空为止。

另一种就是我们一直遍历完队列中的所有顶点。

当前的队头是3，然后将3出队并把和3相邻且没有访问过的入队。并没有新的元素入队，队列元素如下：

46

当前的队头是4，然后将4出队并把和4相邻且没有访问过的入队。并没有新的元素入队，队列元素如下：

6

当前的队头是6，然后将6出队并把和6相邻且没有访问过的入队。并没有新的元素入队，队为空，图的遍历结束。

3 广度优先遍历实现

接下来我们来实现一下上面的过程。

首先我们需要定义图结构，然后实现图的输入和输出：

#include<string.h>
#include<iostream>
using namespace std;

int n,m,k; 
int x,y;

struct Edge {
  int v; //边的终点
  int next; //当前边在邻接表中的下一条边
}e[100];
int vFirst[100]; //每个节点指向的第条边，没有存为-1，邻接表指针
int vis[100]; //表示节点是否被访问过 

void e_push_back(int u,int v)
{
  e[k].v=v; //输入终点
  e[k].next=vFirst[u]; //以u为起点，指向的next是vFirst[u]。
  vFirst[u]=k; //更新u的目前第一个指向的边
  k++; //k为边的序号
}

void print(){ //从顶点的角度输出
  for(int i = 1;i<=n;i++){
    cout<<"["<<i<<"]->"<<e[vFirst[i]].v;
    k = vFirst[i];
    while(e[k].next != -1){
      k = e[k].next;
      cout<<"->"<<e[k].v;
    }
    cout<<endl;
  }
}

int main() {
  memset(vFirst,-1,sizeof(vFirst)); //-1表示空
  cin>>n>>m;
  for(int i=0;i<m;i++) {
    cin>>x>>y;
    e_push_back(x,y);
    e_push_back(y,x); //有向图要存两次
  }
  
  print();
}

上面的代码基本上就相当于我们未来参加信息学竞赛中，图论相关题目的模板了，剩下的就是在上面的基础上做相关调整即可。

我们需要一个队列来辅助进行深度优先遍历，所以我们先定义队列相关的结构和函数：

struct Q{
  int e[100];
  int front,rear; // 队头和队尾 
};

void initQ(Q &q){
  memset(q.e,0,sizeof(q.e));
  q.front = 0;
  q.rear = 0;
} 

void push(Q &q, int a){
  vis[a] = 1;
  q.e[q.rear] = a;
  q.rear++; 
} 

int pop(Q &q){
  q.front++;
  return q.front-1; //保证能获取队头；
}

接下来就是我们的BFS函数了。

首先我们需要先把第一个顶点入队，我们先定义一个队列，然后初始化，然后就可以将第一个顶点入队了：

Q q;
initQ(q);
push(q, x);

然后，我们就可以使用循环的方式不断地将相连的边入队：

void bfs(int x) {
  Q q;
  initQ(q);
  push(q, x);
  while(q.front!=q.rear){
    
  } 
}

在循环体中，我们每次获取队头，将队头出队并输出：

void bfs(int x) {
  Q q;
  initQ(q);
  push(q, x);
  while(q.front!=q.rear){
    x = pop(q);
    cout<<q.e[x]<<" ";
    
  } 
}

通过队头获得目前我们遍历到的顶点，然后将和该顶点相连的其他顶点中未访问的顶点通过循环方式入队：

void bfs(int x) {
  Q q;
  initQ(q);
  push(q, x);
  while(q.front!=q.rear){
    x = pop(q);
    cout<<q.e[x]<<" ";
    for(int i=vFirst[q.e[x]]; i!=-1; i=e[i].next){//遍历每一个相邻的顶点入队 
      if(vis[e[i].v]==0){ //未访问才能入队 
        push(q, e[i].v);
      }
    }
  } 
}

这样我们广度优先遍历算法就完成啦！

整体代码如下：

#include<string.h>
#include<iostream>
using namespace std;

int n,m,k; 
int x,y;

struct Q{
  int e[100];
  int front,rear; // 队头和队尾 
};

struct Edge {
  int v; //边的终点
  int next; //当前边在邻接表中的下一条边
}e[100];
int vFirst[100]; //每个节点指向的第条边，没有存为-1，邻接表指针
int vis[100]; //表示节点是否被访问过 

void e_push_back(int u,int v)
{
  e[k].v=v; //输入终点
  e[k].next=vFirst[u]; //以u为起点，指向的next是vFirst[u]。
  vFirst[u]=k; //更新u的目前第一个指向的边
  k++; //k为边的序号
}

void initQ(Q &q){
  memset(q.e,0,sizeof(q.e));
  q.front = 0;
  q.rear = 0;
} 

void push(Q &q, int a){
  vis[a] = 1; //说明节点访问过 
  q.e[q.rear] = a;
  q.rear++; 
} 

int pop(Q &q){
  q.front++;
  return q.front-1; //保证能获取队头；
}

void print(){ //从顶点的角度输出
  for(int i = 1;i<=n;i++){
    cout<<"["<<i<<"]->"<<e[vFirst[i]].v;
    k = vFirst[i];
    while(e[k].next != -1){
      k = e[k].next;
      cout<<"->"<<e[k].v;
    }
    cout<<endl;
  }
}

void bfs(int x) {
  Q q;
  initQ(q);
  push(q, x);
  while(q.front!=q.rear){
    x = pop(q);
    cout<<q.e[x]<<" ";
    for(int i=vFirst[q.e[x]]; i!=-1; i=e[i].next){//遍历每一个相邻的顶点入队 
      if(vis[e[i].v]==0){ //未访问才能入队 
        push(q, e[i].v);
      }
    }
  } 
}

int main() {
  memset(vFirst,-1,sizeof(vFirst)); //-1表示空
  cin>>n>>m;
  for(int i=0;i<m;i++) {
    cin>>x>>y;
    e_push_back(x,y);
    e_push_back(y,x); //有向图要存两次
  }
  
  bfs(1); //默认从第一个顶点开始访问 
}

例如对于上面的图，输入如下：

6 81 21 52 33 43 54 54 65 6

输出如下：

在这个代码里，我们所有的结构都是自己写的， 我们也可以使用STL库中的函数。

3 广度优先搜索

接下来我们看一下广度优先搜索！

1 广度优先搜索概念

广度优先搜索算法是和深度优先搜索算法类似的非常经典的搜索算法，广度优先遍历算法就是广度优先搜索算法在图论中的直接应用。这一算法也是很多其他重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和广度优先搜索类似的思想。

广度优先算法的核心思想是：

从某一节点开始做如下操作：1、搜索当前节点是否满足需求，2、搜索和第一个节点相关的其他节点；3、循环搜索和上一层节点相关的其他未搜索过的节点。直到达到目标或者全部搜索完为止。‍

‍

2 广度优先搜索框架

根据上面的思想，我们可以写如下的框架：

void bfs(初始节点) {
  初始化队列；
  将初始节点加入队列中
  while(队列不空){
    获取队头节点并出队；
    搜索队头节点；
    for(遍历队头节点相关所有节点) {
      if(当前节点没有搜索过) 将当前节点入队 
    } 
  } 
}

这个框架做法并不唯一，只要思想一致即可。

4 广度优先搜索应用

本节课的作业，就是复习上面的所有知识，并完成下面两道题目！

1 收费站

某个城市有多个收费站；每经过一个收费站，车主就要缴纳一定的费用。

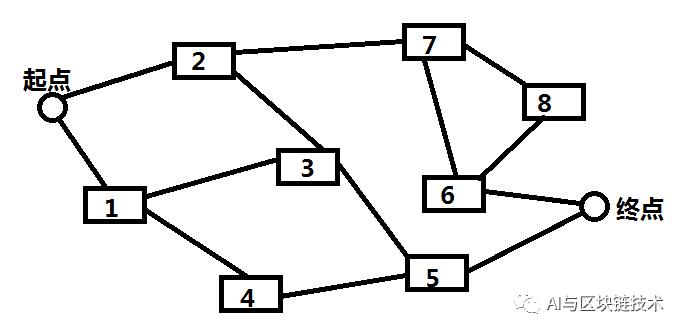
对于上面的这幅图，某个车主得知每个收费站的收费都是a元的，现在需要我们帮助他规划一条路径，告诉他最少的收费情况。

【分析】

这道题目，我们就可以使用广度优先遍历来实现。我们令起点为0，终点为9。我们就可以用如下方式输入，其中，第一行前两个参数表示图的顶点个数和边数，第三个参数是价格a，后面的多行是存在边的顶点：

10 13 100 10 21 31 42 32 73 54 55 96 76 86 97 8

我们知道，每次访问一个节点所有相关的节点，就相当于我们访问比当前节点更深的一层。

当我们第一次访问到终点的时候，当前的层次就是最浅的层次。所以我们记录一下层次，起点的层次设为0。

然后，我们就可以基于上面的代码去完成相关操作了。只需要修改bfs函数即可。

在广度优先遍历过程中，我们要记录每个顶点的层次，其中起点的层次为0，其他顶点的层次就是其相连的第一个顶点的层次+1。假设终点的层次为k，那么就经过了k-1个收费站。

具体代码如下：

int bfs(int x) {
  Q q;
  initQ(q);
  push(q, x);
  while(q.front!=q.rear){
    x = pop(q);
// cout<<q.e[x]<<" ";
    for(int i=vFirst[q.e[x]]; i!=-1; i=e[i].next){//遍历每一个相邻的顶点入队 
      if(vis[e[i].v]==0){ //未访问才能入队 
        push(q, e[i].v);
        dis[e[i].v] = dis[q.e[x]] + 1;
      }
      if(e[i].v == 9){
// cout<<dis[e[i].v]-1<<endl;
        return dis[e[i].v]-1;
      }
    }
  } 
}

全部代码如下：

#include<string.h>
#include<iostream>
using namespace std; 
int n,m,a,k,dis[100]; 
int x,y;
struct Q{
  int e[100];
  int front,rear; // 队头和队尾 
};
struct Edge {
  int v; //边的终点
  int next; //当前边在邻接表中的下一条边
}e[100];
int vFirst[100]; //每个节点指向的第条边，没有存为-1，邻接表指针
int vis[100]; //表示节点是否被访问过 
void e_push_back(int u,int v) {
  e[k].v=v; //输入终点
  e[k].next=vFirst[u]; //以u为起点，指向的next是vFirst[u]。
  vFirst[u]=k; //更新u的目前第一个指向的边
  k++; //k为边的序号
}
void initQ(Q &q){
  memset(q.e,0,sizeof(q.e));
  q.front = 0;
  q.rear = 0;
} 
void push(Q &q, int a){
  vis[a] = 1; //说明节点访问过 
  q.e[q.rear] = a;
  q.rear++; 
} 
int pop(Q &q){
  q.front++;
  return q.front-1; //保证能获取队头；
}
void print(){ //从顶点的角度输出
  for(int i = 1;i<=n;i++){
    cout<<"["<<i<<"]->"<<e[vFirst[i]].v;
    k = vFirst[i];
    while(e[k].next != -1){
      k = e[k].next;
      cout<<"->"<<e[k].v;
    }
    cout<<endl;
  }
}

int bfs(int x) {
  Q q;
  initQ(q);
  push(q, x);
  while(q.front!=q.rear){
    x = pop(q);
// cout<<q.e[x]<<" ";
    for(int i=vFirst[q.e[x]]; i!=-1; i=e[i].next){//遍历每一个相邻的顶点入队 
      if(vis[e[i].v]==0){ //未访问才能入队 
        push(q, e[i].v);
        dis[e[i].v] = dis[q.e[x]] + 1;
      }
      if(e[i].v == 9){
// cout<<dis[e[i].v]-1<<endl;
        return dis[e[i].v]-1;
      }
    }
  } 
}

int main() {
  memset(vFirst,-1,sizeof(vFirst)); //-1表示空
  cin>>n>>m>>a;
  for(int i=0;i<m;i++) {
    cin>>x>>y;
    e_push_back(x,y);
    e_push_back(y,x); //有向图要存两次
  }
  
  int num = bfs(0); //默认从第一个顶点开始访问 
  cout<<num*a<<endl;
}

执行结果如下：

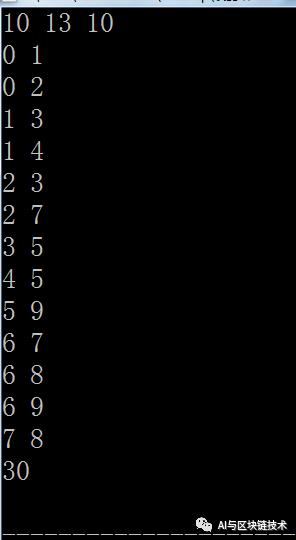
6 作业

本节课的作业，就是复习上面的所有知识，并完成下面的题目！

1 走迷宫

下图是一个迷宫，现在我们需要走一条路径，从左上角走到右下角。其中0表示这个格子可以走，1表示这个格子不能走。

现在要求输出这个地图从起点走到终点最短的路径长度。（每个格子代表1，起点和终点也算到路径中）

AI与区块链技术

长按二维码关注