信息学赛培 | 03 二叉树实战
Posted AI与区块链技术
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了信息学赛培 | 03 二叉树实战相关的知识,希望对你有一定的参考价值。
戳一戳!和我一起走进信息学的世界
导读
信息学能够有助于孩子未来工作发展,提升孩子的综合能力。
上一节课我们系统学习了二叉树的相关理论,了解了相关的性质,掌握了三种遍历方式。这一节课,我们通过代码来更加深入了解二叉树,并实现简单的小功能。
往期回顾
【NOIP竞赛/CSP认证】
【信息学精华帖】
▶
▶
▶
▶
▶
【信息学集训】
【信息学集训】
▶
▶
▶
▶
▶
▶
【数据结构前导课】
▶
【C++提高班教程】
【C++基础班教程】
1 二叉树回顾
上节课,我们学习了树的相关概念,学习了二叉树的相关理论,其中最重要的是二叉树的性质和遍历方法,让我们来回顾一下吧!
1 二叉树的性质
二叉树有如下几条性质:
性质1:有n(n>0)个结点的二叉树的分支数为n-1。
性质2:若二叉树的高度为h(h≥0),则该二叉树最少有h个结点,最多有
性质3:含有n个结点的二叉树的高度最大值为n,最小值为
性质4:具有 n 个结点的完全二叉树的高度为
性质5:如果将一棵有n个结点的完全二叉树自顶向下,同一层自左向右连续给结点编号0、1、2、…、n-1。则第i个结点的左孩子结点的编号是
二叉树有四种遍历方式,分别是:
先序遍历中序遍历后序遍历层次遍历
先序遍历是说对于根节点和左右子节点,先访问根节点,再访问左右子节点。即顺序为根左右。
中序遍历的顺序为左根右;后序遍历的顺序是左右根。
层次遍历是按照层次从上往下,从左往右。
2 二叉树实战
我们通过C++来实现一下二叉树吧!
1 二叉树结构定义
首先我们来定义二叉树的结构。我们围绕两个存储结构,一个是使用顺序表(数组)存储。另一个是使用链式结构存储。
使用顺序表存储非常简单,但是这种方法比较浪费空间。当然,我们只使用单个数组是不行的,我们不知道其子节点对应位置为0时,我们不知道该位置是值为0还是这个位置没有值。我们可以找一个辅助数组,来存放其是否有左右子节点。
struct BiTree{
int data[100];
int child[100]; //无左右为0,只有左为1,只有右为2,左右均有为3
};在竞赛中,我们更多使用链式结构,所以我们着重讲解链式结构。链式结构比较复杂,但是空间占用较小。我们首先需要先定义二叉树的节点,一个比较完整的节点需要有如下几部分:
该节点存放的数据该节点的编号该节点是否被访问该节点的左右子节点该节点的父节点
具体实现如下:
struct BiTNode {
int data; //当前节点的数据
int number; //节点序号,可以没有
int isAsk; //节点是否被访问。
BiTNode * lChild, * rChild, * parent; //左右子节点和父节点指针
};在竞赛中,我们可以使用顺序表辅助构建二叉树,会使得代码更加简洁。
我们把所有的节点存到一个数组中,通过访问索引获得其左右子节点和父节点:
struct BiTNode {
int data; //当前节点的数据
int num; //节点序号
bool isAsk; //节点是否被访问。
int l, r, pr; //左右子节点和父节点指针
};
struct BiTree {
BiTNode a[100];
int num;
} t;一般来说为了方便遍历,我们存储数据,是按照层次遍历存储的。
我们存储使用的初始化输入函数如下:
void init(BiTree &BT){
cin>>BT.len;
for(int i=1;i<=BT.len;i++){
cin>>BT.a[i].num;
cin>>BT.a[i].data;
cin>>BT.a[i].l;
cin>>BT.a[i].r;
cin>>BT.a[i].pr;
BT.a[i].isAsk = 0;
}
}后面我们要对二叉树进行遍历,我们以下面这棵树为例:
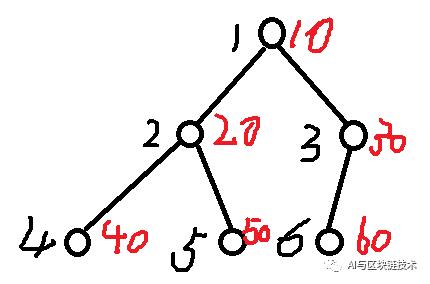
二叉树的先序遍历是按照根左右遍历。
我们采用递归的方式实现,即在每层递归中,先访问当前节点,再递归访问左子节点,再递归访问右子节点:
//先序遍历
void PreOrder(int node) {
if (node)
{
Visit(node);
PreOrder(t.a[node].l);
PreOrder(t.a[node].r);
}
}思想是非常简单的,我们使用编号作为参数去访问。
然后有了这个,我们就可以根据自己的需要去设计Visit函数。例如我们只需要输出其序号和数据:
void Visit(int node) {
cout<<t.a[node].num<<" "<<t.a[node].data<<endl; //也可以输出其他信息
}全部代码如下:
#include<iostream>
using namespace std;
struct BiTNode {
int data; //当前节点的数据
int num; //节点序号
bool isAsk; //节点是否被访问。
int l, r, pr; //左右子节点和父节点指针
};
struct BiTree {
BiTNode a[100];
int len;
} t;
void init(BiTree &BT){
cin>>BT.len;
for(int i=1;i<=BT.len;i++){
cin>>BT.a[i].num;
cin>>BT.a[i].data;
cin>>BT.a[i].l;
cin>>BT.a[i].r;
cin>>BT.a[i].pr;
BT.a[i].isAsk = 0;
}
}
void Visit(int node) {
cout<<t.a[node].num<<" "<<t.a[node].data<<endl; //也可以输出其他信息
}
//先序遍历
void PreOrder(int node) {
if (node)
{
Visit(node);
PreOrder(t.a[node].l);
PreOrder(t.a[node].r);
}
}
int main(){
init(t);
PreOrder(1);
return 0;
}执行结果如下:
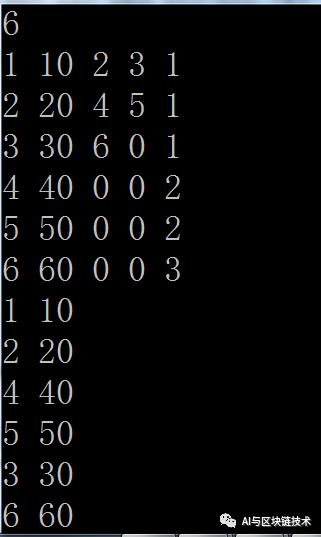
二叉树中序遍历是左根右,我们使用递归方式实现,就是先递归访问左子树,然后访问当前节点,然后递归访问右子树。
所以,递归实现中序遍历只需要在先序遍历的基础上简单修改顺序即可,具体代码如下:
//中序遍历
void InOrder(int node) {
if (node)
{
InOrder(t.a[node].l);
Visit(node);
InOrder(t.a[node].r);
}
}执行结果如下:
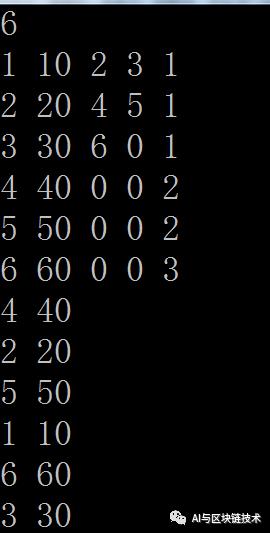
4 二叉树的后序遍历
后序遍历也是一样,先递归访问左子树,然后递归访问右子树,最后访问当前节点。
代码如下:
//后序遍历
void PostOrder(int node) {
if (node)
{
PostOrder(t.a[node].l);
PostOrder(t.a[node].r);
Visit(node);
}
}执行结果如下:
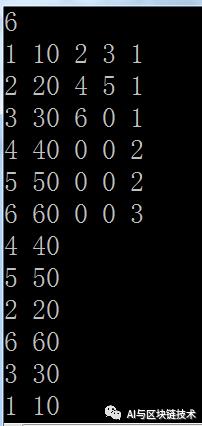
层次遍历最简单,因为我们存储过程中就是按照层次存储的,所以我们就相当于遍历数组即可:
//层次遍历
void LevelOrder() {
for(int i = 1;i<=t.len;i++){
Visit(i);
}
}执行结果如下:
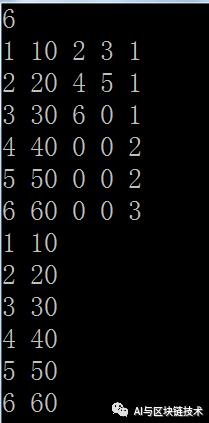
3 二叉树应用
基于上面的代码,我们来做一个简单的应用!
1 判断二叉树是否为完全二叉树
分析
一棵完全二叉树要满足一个节点有子节点,那么其前面的节点必然有两个子节点,如果这个节点只有一个子节点,则必然为左子节点。
如果一棵树不是完全二叉树,我们通过层次遍历,依次访问每个节点的左右子节点,如果我们访问到某个节点的子节点为空,如果后面还有节点,则说明该树不是完全二叉树。
所以我们可以使用层次遍历统计,如果当前节点有左子节点就加1,有右子节点也加一,如果没有,就退出统计,最后比较统计得到的个数和树中节点个数。如果不相等,这说明该树不是完全二叉树。否则就是完全二叉树。
代码
代码如下:
#include<iostream>
using namespace std;
struct BiTNode {
int data; //当前节点的数据
int num; //节点序号
bool isAsk; //节点是否被访问。
int l, r, pr; //左右子节点和父节点指针
};
struct BiTree {
BiTNode a[100];
int len;
} t;
void init(BiTree &BT){
cin>>BT.len;
for(int i=1;i<=BT.len;i++){
cin>>BT.a[i].num;
cin>>BT.a[i].data;
cin>>BT.a[i].l;
cin>>BT.a[i].r;
cin>>BT.a[i].pr;
BT.a[i].isAsk = 0;
}
}
bool isFBT(BiTree BT){
int sum=1; //至少一个根节点
for(int i=1;i<=BT.len;i++){
if(BT.a[i].l) sum++;
else break;
if(BT.a[i].r) sum++;
else break;
}
if(sum == BT.len) return true;
else return false;
}
int main(){
init(t);
if(isFBT(t)) cout<<"是完全二叉树"<<endl;
else cout<<"不是完全二叉树"<<endl;
return 0;
}执行结果如下:
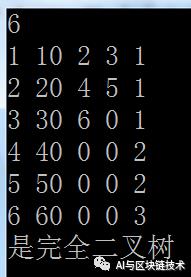
如果我们删除掉一个节点,比如4这个节点,执行结果如下:
6 作业
本节课的作业,就是复习上面的所有知识,并完成下面的题目!
1 求二叉树的高
输入一棵二叉树,求这棵二叉树的高;
AI与区块链技术
长按二维码关注
以上是关于信息学赛培 | 03 二叉树实战的主要内容,如果未能解决你的问题,请参考以下文章
信息学赛培 | 09 总览全局的算法——广度优先搜索算法与实例详解