恋上数据结构与算法第一季笔记——二叉搜索树

Posted 2021-07-24 Johnny*

二叉搜索树

• 二叉搜索树
• • 二叉搜索树的接口实现
• BinarySearchTree
• • BinarySearchTree 属性与构造方法
  • size()
  • isEmpty()
  • add()
• Main类测试
• • 匿名内部类

二叉搜索树

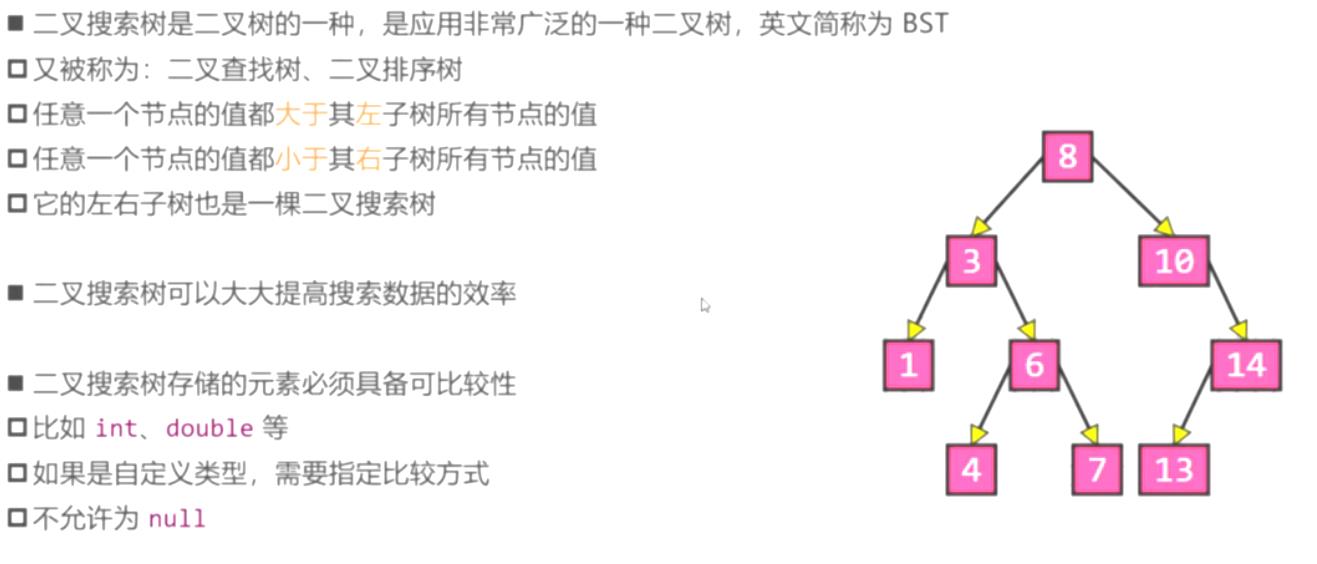
二叉搜索树的接口实现

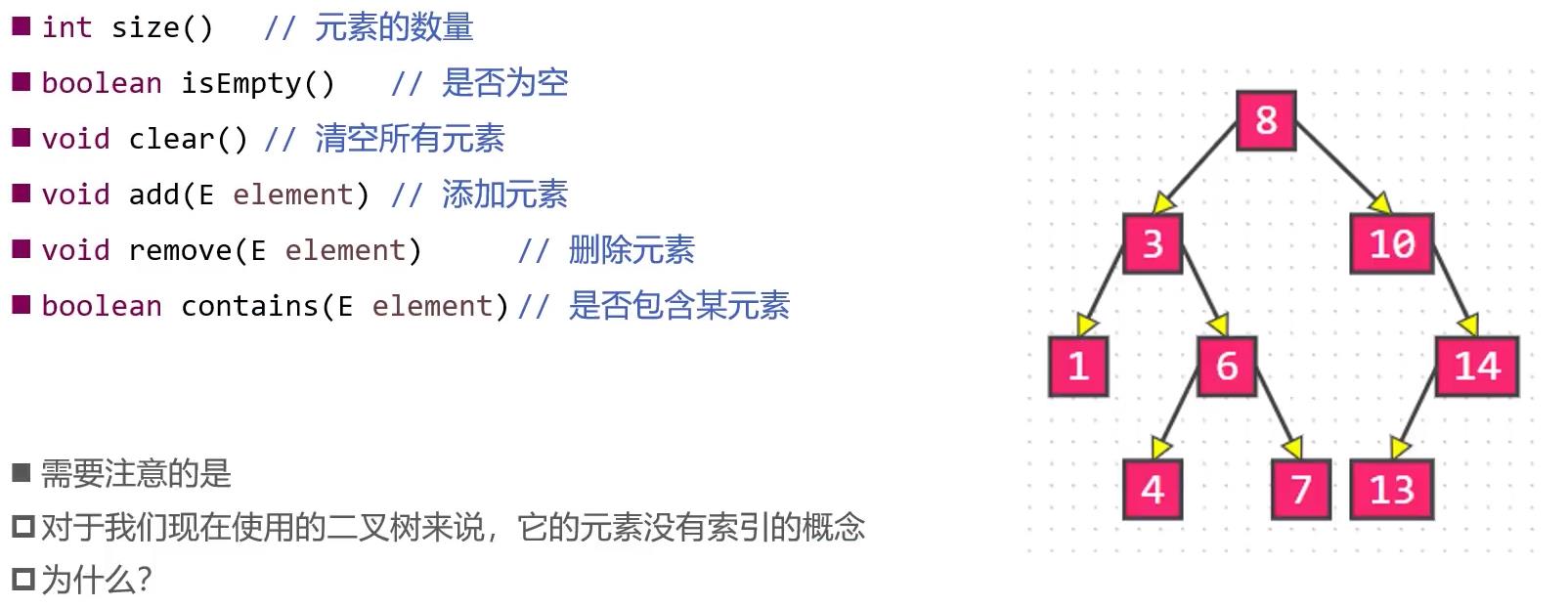
BinarySearchTree

BinarySearchTree 属性与构造方法

 //元素数量
    private int size;
    //二叉搜索树根节点
    private Node root;

    //比较器：由外部定义比较规则，并将比较器传进来使用
    private Comparator comparator;

    //带比较器的构造方法
    public BinarySearchTree(Comparator comparator){
        this.comparator = comparator;
    }

    //不带比较器则默认使用comparable的比较方法
    public BinarySearchTree(){
        this(null);
    }

    //内部类
    private static class Node<E>{

        private Node<E> parent;
        private Node<E> left;
        private Node<E> right;
        private  E element;

        public Node(Node<E> parent, E element){
            this.parent = parent;
            this.element = element;
        }


    }

这里若外部构造BinarySearchTree时使用不传入比较器，则使用Comparable的比较方法，这样比较规则是由内部定义的，除非进入Comparable接口修改比较规则，否则是无法按自定义比较的。
若想自定义比较，则用户可在外部定义比较规则，再使用使用带比较器的构造方法将构造器传进来。

size()

  /**
     * 元素数量
     * @return
     */
    public int size(){
        return size;
    }

isEmpty()

/**
 * 二叉搜索树是否为空
 * @return
 */
public boolean isEmpty(){
    return size == 0;
}

add()

public void add( E element){
        //二叉树树不允许节点为空 插入前先判断
        elementNotNullChck(element);

        //添加第一个节点
        if( root == null){
            root = new Node<>(null, element);
            size ++;
            return ;
        }
        int cmp = 0;
        Node<E> node = root;
        Node<E> parent = root; //记录待插入节点的父节点位置

        //找到待插入节点的父节点
        while( node != null){//非叶子节点的下层

            parent = node;
            cmp = compare( element , node.element);
            /**
             * 待插入节点元素 与当前节点元素值比较：
             * 1.小于则进入左子树
             * 2.大于则进入右子树
             * 3.等于则直接返回
             */
            if( cmp < 0 ) node = node.left;
            else if( cmp > 0) node = node.right;
            else return;

        }
        Node newNode = new Node<>(parent, element);
        if( cmp < 0) parent.left = newNode;
        else parent.right = newNode;
        //最后不要忘记了： 节点数目++
        size ++;


    }
private void elementNotNullChck(E element){
        if( element == null)
            throw  new IllegalArgumentException("element must not be null");
    }
    public int compare(E e1, E e2){
        if( this.comparator == null)
            return ((Comparable)e1).compareTo(e2);
        else
            return this.comparator.compare(e1, e2);

    }

Main类测试

匿名内部类

Comparator是一个接口，本身是不能new的，实际上是有一个匿名类实现的了该接口然后再new。

import java.util.Comparator;



public class Main {
    public static void main(String[] args) {

        //匿名内部类
        BinarySearchTree<Person> bst1 = new BinarySearchTree<>(new Comparator<Person>() {
            @Override
            public int compare(Person o1, Person o2) {
                return o1.getAge() - o2.getAge();
            }
        });

    }
}

作用于上面等效不过，上面代码较为紧凑，不用声明类PesonComparator 实现Comparator接口

import java.util.Comparator;



public class Main {

    static class PesonComparator implements Comparator<Person> {
        @Override
        public int compare(Person o1, Person o2) {
            return o1.getAge() - o2.getAge();

        }
    }
    public static void main(String[] args) {



        BinarySearchTree<Person> bst = new BinarySearchTree<>( new PesonComparator()) ;
        bst.add( new Person(52));
        bst.add( new Person(25));

    }
}