数据结构与算法（二叉搜索树）~ 介绍二叉搜索树以及力扣上几道二叉搜索树题目的方法和套路

Posted 2021-10-27 一乐乐

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构与算法（二叉搜索树）~ 介绍二叉搜索树以及力扣上几道二叉搜索树题目的方法和套路相关的知识，希望对你有一定的参考价值。

数据结构与算法（二叉搜索树）~ 介绍二叉搜索树以及力扣上几道二叉搜索树题目的方法和套路

1，二叉树的数据结构：

请参考文章：《数据结构与算法（二叉树）~ 介绍二叉树以及力扣上几道二叉树题目的方法和套路~ 第一部分》

❀ 二叉搜索树的特点：

● 整个二叉搜索树非常有特点，根大于左子树，小于右子树

● 二叉搜索数的中序遍历是有序的~升序的

✿ 总结一些小套路吧（没有通用的套路，就讲一下方法哈）：

（1）108_将有序数组转换为二叉搜索树的方法和套路：

方法一：利用二叉搜索树特点：根大于左，小于右【将数组不断地按中间点划分成左右子树】

（2）173_二叉搜索树迭代器的方法和套路：

方法一：迭代器（容器，提前存储了按照一定规则摆放的数据~ 中序遍历（递归））,然后定义一个全局索引变量来辅助是否有next和进入next

方法二：迭代器（容器，提前存储了按照一定规则摆放的数据~ 中序遍历（迭代））,然后定义一个全局索引变量来辅助是否有next和进入next~因为题意要最小的，所以next方法，next到最后一层后【左为null】，该值【根】便是所求，然后切换到右边

（3）230_二叉搜索树中第K小的元素的方法和套路：

方法一：中序遍历【递归法~辅助变量，递归到第k次便是所求】

方法二：中序遍历【迭代法~辅助变量，pop掉k个数，便是所求】

（4）450_删除二叉搜索树中的节点的方法和套路：

方法一：

//删除值大于根值，则只能在左子树删除目标，删除值小于根值，只能子啊右子树删除目标。

//当删除的目标就是根值时，考虑：① 根是叶子【根置空】 ② 有右子树【根用后驱结点值覆盖，然后对右子树的重复结点进行删除】

③ 没有右子树【只能到左子树找了，根用前驱结点值覆盖，然后对左子树的重复结点进行删除】

（5）530_二叉搜索树的最小绝对差的方法和套路：

方法一：

方法二：

套路一：

（6）700_二叉搜索树中的搜索的方法和套路：

方法一：

方法二：

套路一：

（7）701_二叉搜索树中的插入操作的方法和套路：

方法一：

方法二：

套路一：

（8）783_二叉搜索树节点最小距离的方法和套路：

方法一：

方法二：

套路一：

（9）938_二叉搜索树的范围和的方法和套路：

方法一：

方法二：

套路一：

（10）98_验证二叉搜索树的方法和套路：

方法一：

方法二：

套路一：

（11）99_恢复二叉搜索树的方法和套路：

方法一：

方法二：

套路一：

数据结构与算法通俗易懂讲解二叉搜索树插入删除

在二叉搜索树查找（请戳我）一文中主要介绍了二叉搜索树的查找,本文将继续介绍其插入和删除操作。二叉搜索树的插入和删除关键在于在插入和删除的过程中如何继续保持二叉搜索树的性质。
二叉搜索树结点定义如下：

typedef struct BSTreeNode{
    Type   key;                 // 关键字(键值)
    struct BSTreeNode *left;    // 左孩子
    struct BSTreeNode *right;   // 右孩子
    struct BSTreeNode *parent;  // 父结点
}Node, *BSTree;

插入结点

插入结点的位置对应着查找过程中查找不成功时候的结点位置，因此需要从根结点开始查找带插入结点位置，找到位置后插入即可。下图所示插入结点过程：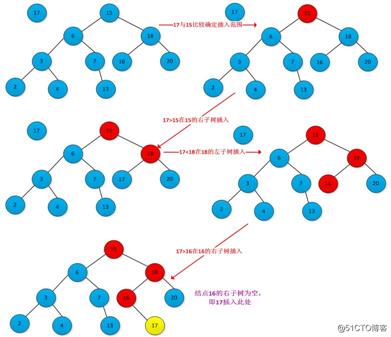
技术图片

插入结点代码如下

//往树tree的插入结点z
Node* bstree_insert(BSTree tree, Node *z)
{
    Node *y = NULL;
    Node *x = tree;

    // 查找z的插入位置
    while (x != NULL)
    {
        y = x;
        if (z->key < x->key)
            x = x->left;
        else
            x = x->right;
    }

    z->parent = y;
    if (y==NULL)
        tree = z;
    else if (z->key < y->key)
        y->left = z;
    else
        y->right = z;

    return tree;
}

删除结点

二叉搜索树删除结点可以说是二叉搜索树中最为复杂的操作，要考虑的情况比较多，下面分情况讨论。
（1）要删除的结点z为叶子结点，这是最简单的一种情况，直接修改其父节点相应指针为NULL。删除过程如下图所示：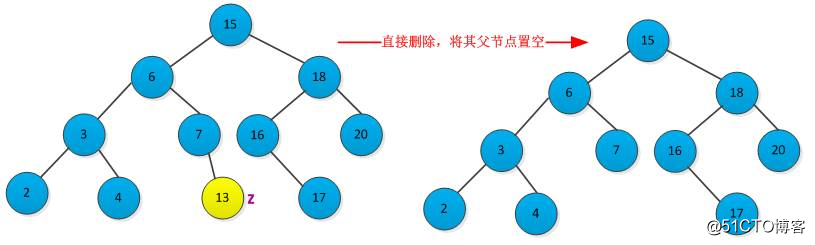
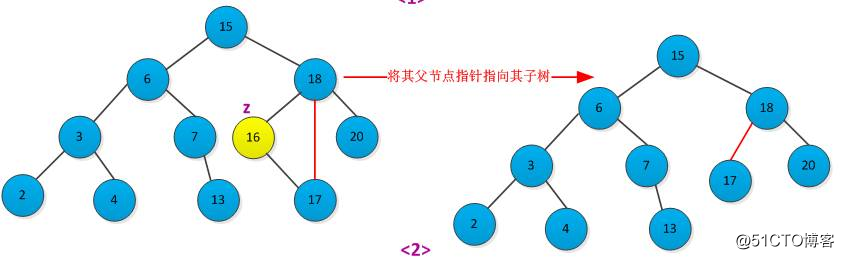
技术图片

（2）要删除的结点z为只有一个子树，让z的子树与z的父亲节点相连，删除z即可，删除过程如下图所示：

技术图片
（3）要删除的结点z为有两个子树，则先找到z的后继结点y，y肯定是没有左子树的(如果y还有左子树，那么y就肯定不是z的后继结点)，所以现在可以按照上面两种情况删除y结点，最后用y的值代替z的值。整个删除过程如下图所示：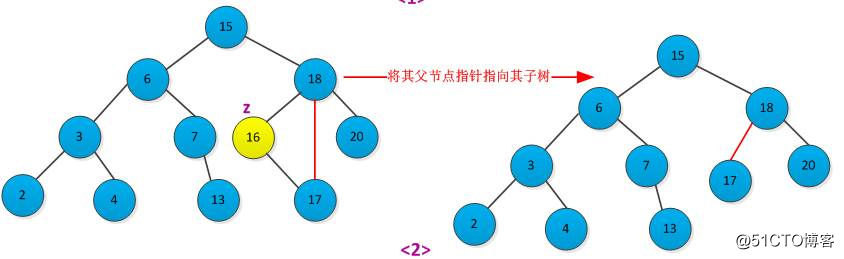
技术图片

二叉搜索树删除结点的代码实现如下。

//删除树tree的结点z
Node* bstree_delete(BSTree tree, Node *z)
{
    Node *x=NULL;
    Node *y=NULL;

    if ((z->left == NULL) || (z->right == NULL))
        y = z;
    else
        y = bstree_successor(z);//找到z的后继结点

    if (y->left != NULL)
        x = y->left;
    else
        x = y->right;

    if (x != NULL)
        x->parent = y->parent;

    if (y->parent == NULL)
        tree = x;
    else if (y == y->parent->left)
        y->parent->left = x;
    else
        y->parent->right = x;

    if (y != z) 
        z->key = y->key;

    if (y!=NULL)
        free(y);

    return tree;
}

代码中的bstree_successor(z)函数功能是找到结点z的后继结点，至于什么是后继结点以及其实现，前文二叉搜索树查找（请戳我）已有总结，此处不再详述。

上面就是二叉搜索树的插入和删除结点的思路和代码，大家在看代码的时候可以对着图将每种情况在自己脑中运行，比如说对于删除操作的第一种情况，它在代码中的运行流程是什么，这样可能更加容易理解。