算法---动态规划（背包问题分割回文串）

Posted 2021-07-18 Moua

第9题：背包问题

问题分析

• 问题分解

      

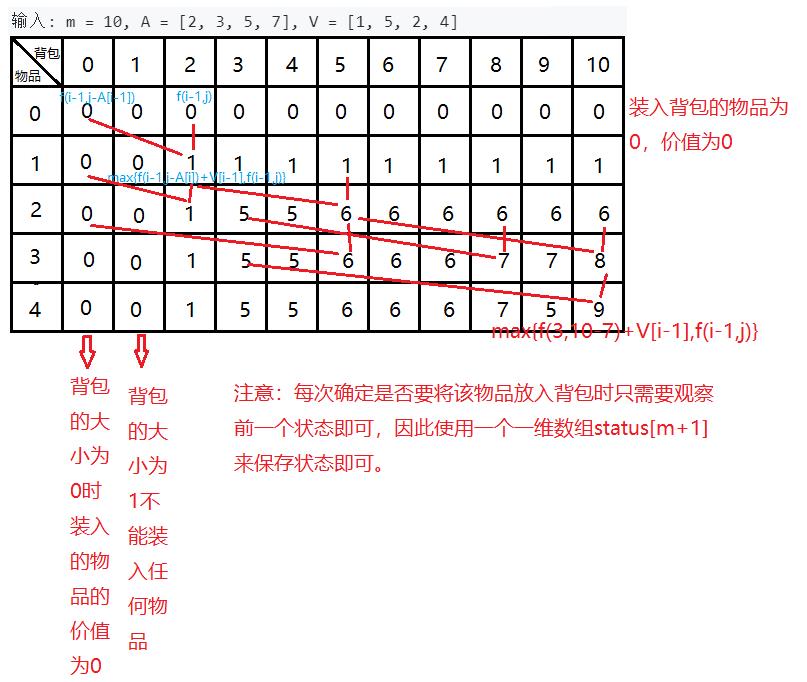
• 状态定义：将i个物品放入大小为j的背包中可以放入的最大总价值f(i,j)
• 状态之间的转化方程

        

• 初始状态：f(0,j) = f(j,0) = 0;即包的大小为0或者放入的物品价值为0时，总价值为0.
• 返回结果：f(n,m)将n个物品放入大小为j的背包的最大总价值
• 举例分析：n = 4,m = 10,A = {2,3,5,7} ,V = {1,5,2,4}

       

代码描述

class Solution {
public:
    /**
     * @param m: An integer m denotes the size of a backpack
     * @param A: Given n items with size A[i]
     * @param V: Given n items with value V[i]
     * @return: The maximum value
     */
    int backPackII(int m, vector<int> &A, vector<int> &V) {
        int len = A.size();
        vector<int> status(m+1,0);//保存状态,初始状态：当放入背包的物品为0时总价值为0
        vector<int> ret(m+1,0);//返回结果：ret[m]
        //状态之间的转换：f(i,j) = max{f(i-1,j),f(i-1,j-A[i-1])+V[i-1]}
        for(int i = 1;i <= len;i++)
        {
            for(int j = 1;j <= m;j++)
            {
                if(A[i-1] > j)
                    ret[j] = status[j];
                else
                    ret[j] = max(status[j],status[j-A[i-1]]+V[i-1]);
            }
            //更新状态
            status = ret;//将ret保存在status中（ret的大小会变成0）
            if(i != len-1)
                ret.resize(m+1,0);//重新对ret初始化
        }
        return ret[m];
    }
};

第10题：分割回文串II

题目分析

• 状态定义：将前i个字符分割成回文串的最小分割次数。
• 状态之间的转移方程：f(i) = f(j)+1;(1 <= j <= i)

将字符串分割成回文串的最小分割次数可以转化为将字符串前i个字符分割成回文串的最小分割次数。

当i = i+1时，有以下几种情况：

1. 第i+1个字符可以和前i个字符组成回文串

         存在一个j，j<i，1~j可以分成回文串，且j+1,i+1可以分割成回文串。j越小f(i+1)就越大，当j = 1时，f(i+1) = 1取最小值。

         因此，有f(i+1) = f(j)+1,(j < i && i < length)

1. 第i+1个字符不可以和前i个字符组成回文串

         f(i+1) = f(i)+1，表示前i个字符的分割次数不变，将第i+1个字符单独分成一个。

• 初始状态：f(1) = 0，将第一个字符分割成回文串的最小分割次数为0.
• 返回结果：f(n)，n为字符串的长度

代码描述

class Solution {
public:
    /**
     * 
     * @param s string字符串 
     * @return int整型
     */
    bool isPalindrome(string& s,int beginIndex,int endIndex)
    {
        while(beginIndex < endIndex)
        {
            if(s[beginIndex] == s[endIndex])
            {
                beginIndex++;
                endIndex--;
            }
            else
                return false;
        }
        return true;
    }
    int minCut(string s) {
        int len = s.size();
        vector<int> minCutI(len+1,0);//保存状态,初始状态f(1) = 0;
        for(int i = 2;i <= len;i++)
        {
            //先判断[1,i]整体是否是回文串
            if(isPalindrome(s,0,i-1))
            {
                minCutI[i] = 0;
            }
            else
            {
                //判断j,i是否为回文串的最小分割次数
                int min = i-1;
                for(int j = 2;j <= i;j++)
                {
                    if(isPalindrome(s,j-1,i-1))
                    {
                        if(minCutI[j-1]+1 < min)
                            min = minCutI[j-1]+1;
                    }
                }
                minCutI[i] = min;
            }
        }
        return minCutI[len];
    }
};