二叉树的中后序遍历构建及求叶子

Posted 2021-07-18 一腔诗意醉了酒

题目描述
按中序遍历和后序遍历给出一棵二叉树，求这棵二叉树中叶子节点权值的最小值。

输入保证叶子节点的权值各不相同。

输入
第一行输入一个整数t，表示有t组测试数据。

对于每组测试数据，首先输入一个整数N (1 <= N <= 10000)，代表二叉树有N个节点，接下来的一行输入这棵二叉树中序遍历的结果，最后一行输入这棵二叉树后序遍历的结果。

输出
对于每组测试数据，输出一个整数，代表二叉树中叶子节点权值最小值。

样例输入
3
7
3 2 1 4 5 7 6
3 1 2 5 6 7 4
8
7 8 11 3 5 16 12 18
8 3 11 7 16 18 12 5
1
255
255
样例输出
1
3
255

解题关键：
先明确，我们建树一般是通过前序遍历的顺序建的。

前序遍历： 根–>左孩子 --> 右孩子
中序遍历： 左孩子–>根 --> 右孩子
后序遍历： 左孩子 --> 右孩子–>根

所以，当我们已知中序遍历以及后序遍历的结果时，我们就可以通过找出一定的规律解题，比如后序遍历的结果的最后一个元素一定是根节点。
如图：

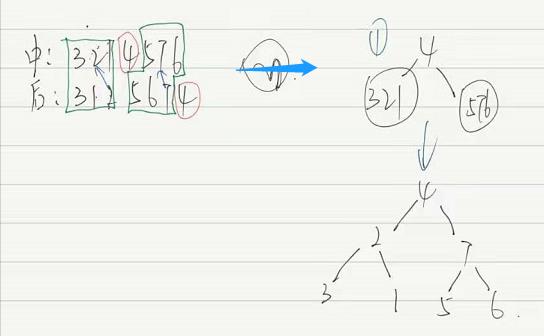
我们发现，在中序遍历结果中，根节点的左边元素为左子树，右元素是右子树。故可以递归得出最后的建树结果。

附：例题C++代码

#include<iostream>
#include<algorithm>

using namespace std;
int *m;
int *h;
int len;
int ans;

class BiTreeNode{
	public:
		int data;
		BiTreeNode *lChild;
		BiTreeNode *rChild;
		BiTreeNode():lChild(NULL),rChild(NULL){};
		~BiTreeNode(){};
};

class BiTree{
	private:
		BiTreeNode *root;
		BiTreeNode * createBiTree(int *mid, int *last, int n);
		void getMin(BiTreeNode *t);
	public:
		BiTree(){};
		~BiTree(){};
		void createTree(); 
		void getMin();
};

void BiTree::createTree(){
	root = createBiTree(m,h,len);
}

BiTreeNode* BiTree::createBiTree(int *mid, int *last, int n){
    if(n==0){
        return NULL;
    }
    BiTreeNode* T = new BiTreeNode();
    int i;
    T->data = last[n-1];
    for(i=0; mid[i]!=last[n-1]; i++);
    T->lChild = createBiTree(mid,last,i);
    T->rChild = createBiTree(mid+i+1,last+i, n-i-1);
	return T;
}

void BiTree::getMin(){
	getMin(root);
}

void BiTree::getMin(BiTreeNode *t){ 
    if(t){
        if(!t->lChild && !t->rChild){
            ans = min(ans,t->data);
        }
        getMin(t->lChild);
        getMin(t->rChild);
    }
}

int main(){
	int Nt;
	cin >> Nt;
	while(Nt--){
        ans = 99999999;
        cin>>len;
        m = new int[len];
        h = new int[len];
        for(int i=0; i<len; i++){
            cin>>m[i]; 
        }
        for(int i=0; i<len; i++){
            cin>>h[i];
        }	
        
        BiTree *bt = new BiTree();
        bt->createTree();
        bt->getMin();
        cout<<ans<<endl;

	}


	return 0;
}