MLP多层感知器pytorch实现过程

Posted 2021-07-17 黑丝太白

参考博客：
https://blog.csdn.net/xholes/article/details/78461164
https://www.pianshen.com/article/1392309515/

代码github地址
使用pytorch框架实现MLP。为了深入了解源码，没有使用pytorch中torch.nn.Module类和其它现有的方法，大部分功能手写实现。

data文件夹中是数据集。

ReLU_CELF.py 是代码，激活函数使用ReLU，损失函数使用交叉熵。

”MLP文档“文件夹中有实现过程与编写代码时遇到的错误，实现过程中的内容与下文一致，实现过程中包括手写。

多层感知机：Multi-Layer Perceptron

多层感知机构建步骤：

1. 构建网络模型
2. 权重初始化
3. 前向传播
4. 计算损失
5. 反向传播求梯度
6. 更新权重

1. 构建网络模型

多层神经网络中第一层称之为输入层，最后一层称之为输出层，中间的层称之为隐层。在分类模型中，输出层的每一个变量对应一个类别。层与层之间两两单元之间存在连接。

在本模型中输入是一个$28\times 28$的图片，所以输入层大小是784，中间两个隐层大小分别是512，128。因为该模型用于识别MNIST手写集，相当于十分类，输出层大小为10。

2. 权重初始化

使用python中的randn来进行权重初始化。

$torch.randn$ 返回一个包含了从标准正态分布中抽取的一组随机数的张量。

def init_parameters(self):
    self.W.append(torch.randn(self.hidden1_size, self.input_size))
    self.W.append(torch.randn(self.hidden2_size, self.hidden1_size))
    self.W.append(torch.randn(self.output_size, self.hidden2_size))
    self.b.append(torch.randn(self.hidden1_size, 1))
    self.b.append(torch.randn(self.hidden2_size, 1))
    self.b.append(torch.randn(self.output_size, 1))

在使用ReLU函数时，权值初始化出现问题。如果输入的x比较大，初始化权值w也比较大，那么就会导致计算出的a比较大，会出现很大的负数或者正数。导致最终计算经过softmax函数后的输出层时，会出现很多值为0，一个值为1的情况，这样对计算loss值是非常不利的，因为会计算$log(0)$。

同时，如果w值比较大的话，还可能会出现梯度爆炸的问题。

最后使用 小随机数或者除$\sqrt{n}$ 的方法来解决，将权重初始化为比较小的值。

def init_parameters(self):
        self.W.append(
            0.01 * torch.randn(self.hidden1_size, self.input_size))
        self.W.append(
            0.01 * torch.randn(self.hidden2_size, self.hidden1_size))
        self.W.append(
            0.01 * torch.randn(self.hidden3_size, self.hidden2_size))
        self.W.append(
            0.01 * torch.randn(self.output_size, self.hidden3_size))
        self.b.append(0.01 * torch.randn(self.hidden1_size, 1))
        self.b.append(0.01 * torch.randn(self.hidden2_size, 1))
        self.b.append(0.01 * torch.randn(self.hidden3_size, 1))
        self.b.append(0.01 * torch.randn(self.output_size, 1))

3. 前向传播

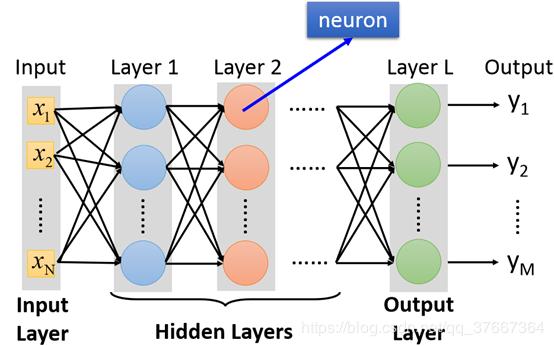
设变量的上标代表所处的神经网络的第几层。

$W^l$连接第$l$层到第$l-1$层的权重矩阵中，其中$W_{ji}^l$表示第$l-1$层的第$i$个节点与第$l$层的第$j$个节点的权重。

$z_j^{l+1}={\sum }_{i=1}^n{w}_{ji}^{l+1}{a}_i^l=w_{j1}^{l+1}{a}_1^l+w_{j2}^{l+1}{a}_2^l+w_{j3}^{l+1}{a}_3^l+...+w_{jn}^{l+1}{a}_n^l$

$a_j^l=f(z_j^l)$，其中$f(\cdot )$为激活函数。

将上述式子转化成矩阵表达式
$$\{\begin{array}{l}{\mathbf{Z}}^l={\mathbf{W}}^l{\mathbf{a}}^{l-1}+{\mathbf{b}}^l\\ {\mathbf{a}}^l=f({\mathbf{z}}^{\mathbf{l}})\end{array}$$

4. 计算损失

使用交叉熵作为损失函数

设我们预测的结果是$\hat{Y}$是我们预测的结果，$Y$是真实分类情况的one-hat编码。

则 $L=-\sum _{i=1}^n{y}_{i}log{\hat{y}}_i$

注意这里的$\hat{Y}$应该是经过softmax函数处理之后的输出，这样能保证 $\sum _{i=1}^n=1$

5. 反向传播与更新参数

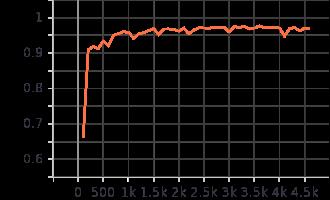
训练过程可视化

使用pytorch内置的Tensorboard进行绘图

训练过程展示，每100个batch绘制一个点

Train_Loss

Train_Accuracy

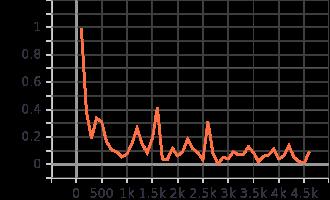
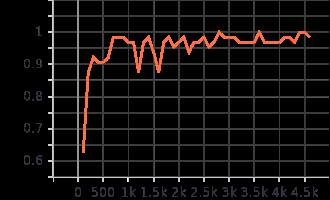
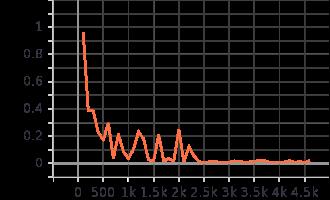
测试过程展示，每100个batch绘制一个点

Test_Loss

Test_Accuracy

​