matlab基于差分进化算法的函数优化分析matlab优化算法九

Posted 2021-06-30 张叔zhangshu

差分进化算法概述

20世纪60年代初，美国 Michigan大学的.Holland教授借鉴与生物进化机制提出了自适应机器人学习，即成为后来广受人们关注的遗传算法； I Rechenberg和 LL.Foge等人都面临着各自研究领域所遇到的复杂问题，受生物种群进化过程和生物习性的启发，分别提岀了进化策略（ES evolutionary strategies）和进化规则（ EP–evolutionary programming）。后来学者们把这类仿生算法统一称为“进化计算”（ evolutionary computation）。
现行的智能算法的普及与应用，得力于计算机技术的普及，计算机性能的提升，使得生物进化算法得意蓬勃发展。生物进化算法能够解决传统算法所不能解决的问题，用户只需要根据自己的工程问题，建立好相应的数学模型，这个数学模型对变量的个数无限制，对于变量约束条件无限制（
前提是合理的约束条件），对于目标函数的多重性无限制，运行进化算法能够很轻易的进行求解，并且给岀较为精确的解以及满意解。经过大量的学者应用研究，基于生物智能算法，利用计算机帮助寻找和判断最佳方案或最优参数，已经在科学硏究、工程设计、经济管理中发挥着越来越大的作用，并且产生了直接、巨大的经济效益。
差分进化算法（DE算法）的主要特性是通过个体间的差异实现个体变异。变异向量由随机选取的个体向量与另外两个随机选取的个体间的差向量求和得到。相比于经典的变异算子，更加贴近个体重组的变异算子的差分是DE算法特有的。DE算法的这个主要特性是由于在它进行变异的时候有一个自我参照的变异向量，使得它在搜索空间内能够循序渐进的搜索。
由于进化算法自身的特点，是基于优胜劣汰的自然选择原理对种群中的个体进行淘汰和保留，因此算法本身具有一定的自组织、自学习、自适应等特点，其寻优方式很容易在多种领域中得到应用差分进化算法（DE算法）和其它生物智能算法（粒子群算法PSO、遗传算法GA等）一样，也容易陷入局部最优，主要归结为生物进化算法均类比于暴力搜索算法，采用初始的种群进行有限的迭代寻优，进而找出相对有效的最优解作为用户满意解。当然这个过程是有增益的，然而当寻优次数增大时，生物智能算法是全局收敛的，因此保证生物个体的多样性以及增大生物进化代数都极大的影响着算法全局寻优能力。

差分进化算法的基本原理

DE算法的实现步骤如下对于求解具有n个连续变量的全局优化问题。可将全局优化问题转化为求解如下函数的最小值问题

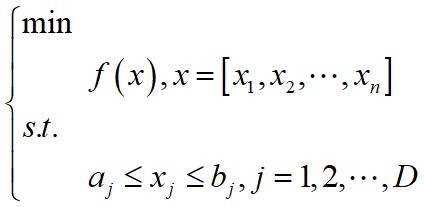
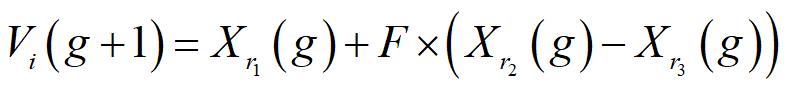
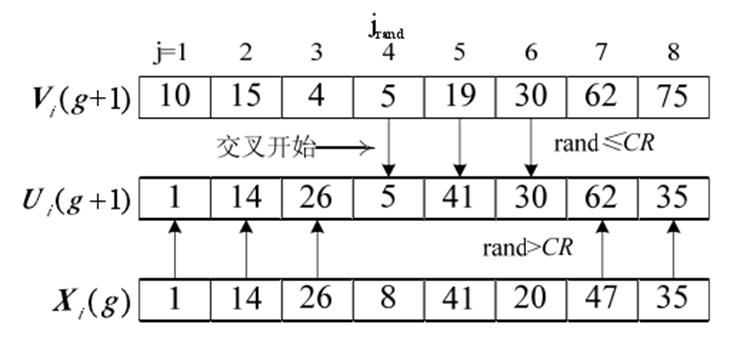
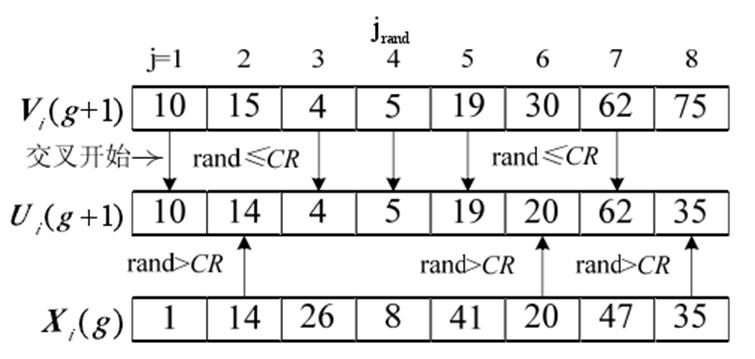
算法流程图

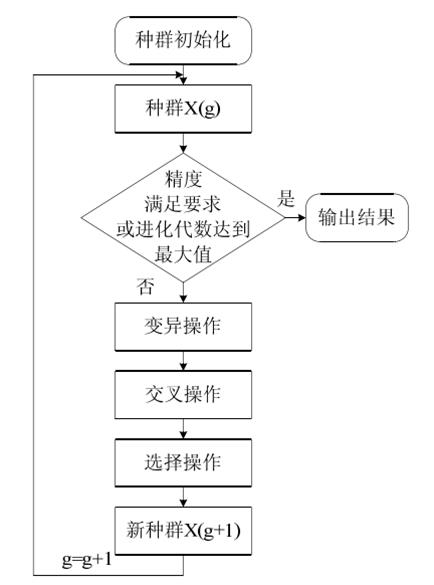
基于DE算法的函数优化与 MATLAB实现

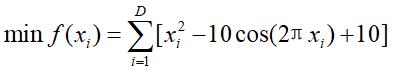
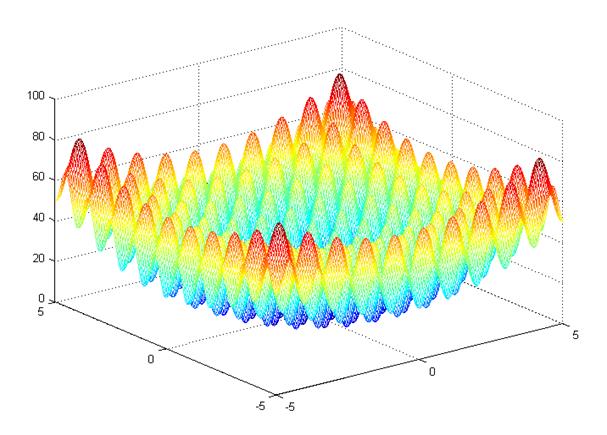
%% DE
%% 清空环境变量
clc,clear,close all
warning off
feature jit off
F0 = 0.5;  % 是变异率    
Gm = 100;  % 最大迭代次数
Np = 100;  % 种群规模
CR = 0.9;  % 杂交参数
G = 1;     % 初始化代数
N = 10;    % 所求问题的维数，即待求解未知数个数
ge = zeros(1,Np);    % 各代的最优目标函数值
bestx = zeros(Np,N); % 各代的最优解
% 解范围
xmin = -5.12; % 下限
xmax = 5.12;  % 上限
% 产生初始种群
X0 = (xmax-xmin)*rand(Np,N)+xmin;
X = X0;
% 候选解初始化
X1new = zeros(Np,N);  % 初始化
X1_new = zeros(Np,N); % 初始化
X1 = zeros(Np,N);     % 初始化
value = zeros(1,Np);  % 初始化
while G<=Gm   % 迭代开始
    disp(['迭代次数：  ',num2str(G)])
    
    for i=1:Np
        %产生j,k,p三个不同的数
        a=1;b = Np;
        dx = randperm(b-a+1)+a-1;
        j=dx(1);k=dx(2);p=dx(3);
        if j==i
            j=dx(4);
        elseif k==i
            k=dx(4);
        elseif p==i
            p=dx(4);
        end

        % 变异算子
        namd=exp(1-Gm/(Gm+1-G));
        F=F0*2.^namd;

        bon = X(p,:)+F*(X(j,:)-X(k,:)); % 个体更新
        if (bon>xmin)&(bon<xmax)        % 防止变异超出边界
            X1new(i,:)=bon;
        else
            X1new(i,:)=(xmax-xmin)*rand(1,N)+xmin;
        end
    end
    % 杂交操作
    for i=1:Np
        if rand>CR   % 利用二项分布来交叉
            X1_new(i,:)= X(i,:);
        else
            X1_new(i,:) = X1new(i,:);
        end
    end
    % 竞争操作
    for i=1:Np
        if fitness(X1_new(i,:))<fitness(X(i,:))
            X1(i,:)=X1_new(i,:);
        else 
            X1(i,:)=X(i,:);
        end
    end
   % 找出最小值
    for i=1:Np
        value(i)=fitness(X1(i,:));
    end
    [fmin,nmin]=min(value);
    ge(G)=fmin;
    bestx(G,:) = X1(nmin,:); 
    G=G+1;
    X = X1;
end
bestx(end,:)  % 函数最优解
ge(end)

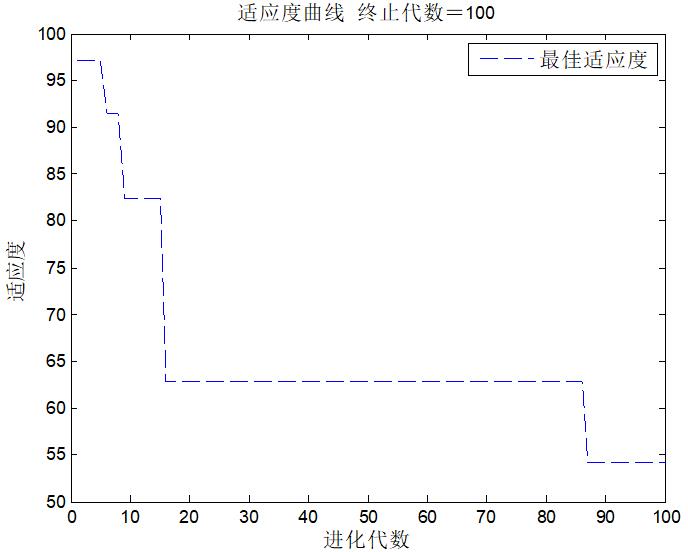
%% 差分进化算法结果分析 
figure('color',[1,1,1]),
plot(1:length(ge),ge,'b--');
title(['适应度曲线  ' '终止代数＝' num2str(Gm)]);
xlabel('进化代数');   ylabel('适应度');
legend('最佳适应度');

下载地址https://download.csdn.net/download/weixin_46567845/19814272