log likelihood为负
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了log likelihood为负相关的知识,希望对你有一定的参考价值。
用stata做logit回归,Log likelihood 值为多少比较正常?说明什么问题?对300多个数据做回归,十几个变量,log likelihood是负的一百多
参考技术A -100多可以的,如果significant的话问题不大二次代价函数交叉熵(cross-entropy)对数似然代价函数(log-likelihood cost)
二次代价函数
$C = frac{1} {2n} sum_{x_1,...x_n} |y(x)-a^L(x) |^2$
其中,C表示代价函数,x表示样本,y表示实际值,a表示输出值,n表示样本的总数;整个的意思就是把n个y-a的平方累加起来,再除以2求一下均值。
为简单起见,先看下 一个样本 的情况,此时二次代价函数为:$C = frac{(y-a)^2} {2}$
$a=sigma(z), z=sum w_j*x_j +b$ ,其中a就代表激活函数的输出值,这个符号$sigma$代表sigmoid函数将变量映射到0-1的$S$型光滑的曲线,z是上一层神经元信号的总和
假如我们使用梯度下降发(Gradient descent)来调整权值参数的大小,权值w和权值b的梯度推到如下(求导数):
$frac {partial C} {partial w} = (a-y)sigma‘ (z)x$ $frac {partial C} {partial b} = (a-y)sigma‘ (z)$
其中,z表示神经元的输入,$sigma$表示激活函数sigmoid。可以看出,w和b的梯度跟激活函数的梯度成正比,激活函数的梯度越大,w和b的大小调整越快,训练收敛的就越快。
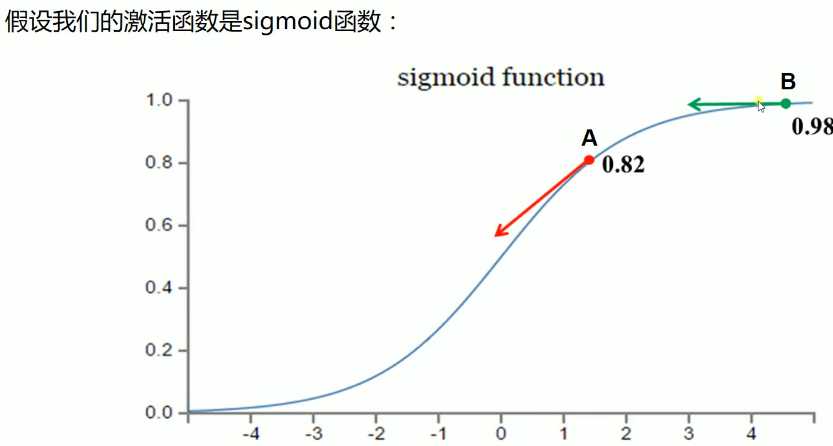
假设我们激活函数输出的值目标是收敛到1,A点离目标较远,梯度较大,权值调整比较大。B点为0.98离目标比较近,梯度比较小,权值调整比较小,调整方案合理。
假设我们激活函数输出的值目标是收敛到0,A点离目标较远,梯度较大,权值调整比较大。B点为0.98离目标比较远,梯度比较小,权值调整比较小,调整方案不合理,B点要经过非常长的时间才会收敛到0,而且B点很可能成为不收敛的点。
交叉墒代价函数(cross-entropy)
由于上边的问题,我们换一种思路,我们不改变激活函数,而是改变代价函数,改用交叉墒代价函数:
$C = -frac{1}{n} sum_{x_1,,,x_n}, [yln a + (1-y) ln(1-a)]$
其中,C表示代价函数,x表示样本,y表示实际值,a表示输出值,n表示样本的总数。
$a=sigma(z), z=sum w_j*x_j +b $ $ sigma‘(z) = sigma(z)(1-sigma (x))$ sigmod函数的导数比较好求,这也是为什么大家用sigmoid做激活函数的原因,接下来我们看一下求导的过程
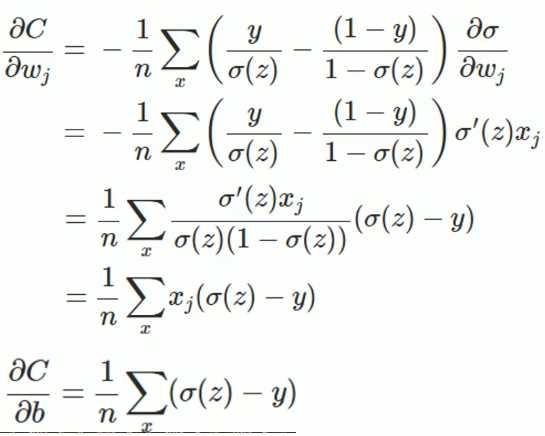
懒得敲了,直接贴个图过来,之后闲了在敲一遍,上边就是求导的推导过程,从最后的式子可以看出:权值w和偏执值b的调整与$sigma ‘(z)$无关,另外,梯度公式中的$sigma (z)-y$表示输出值与实际值放入误差。所以当误差越大时,梯度就越大,参数w和b的调整就越快,训练的速度也就越快。
总结:当输出神经元是线性的,那么二次代价函数就是一种合适的选择。如果输出神经元是S型函数,那么比较适合交叉墒代价函数。
对数似然代价函数(log-likelihood cost)
对数似然函数常用来作为softmax回归的代价函数,如果输出层神经元是sigmoid函数,可以使用交叉墒代价函数。而深度学习中更普遍的做法是将softmax作为最后一层,此时常用的代价函数是对数似然代价函数。
对数似然代价函数与softmax的组合和交叉墒与sigmoid函数的组合非常相似。对数似然代价函数在二分类时可以化简为交叉墒代价函数的形式。
在TensorFlow中用:
tf.nn.sigmoid_cross_entropy_with_logits()来表示跟sigmoid搭配使用的交叉墒。
tf.nn.softmax_cross_entropy_with_logits()来表示跟softmax搭配使用的交叉墒。
以上是关于log likelihood为负的主要内容,如果未能解决你的问题,请参考以下文章
R语言构建logistic回归模型并使用对数似然(log likelihood)评估概率模型:对数似然(log likelihood)会惩罚预测和真实类标签之间的不匹配预测模型与空模型的对数似然对比
二次代价函数交叉熵(cross-entropy)对数似然代价函数(log-likelihood cost)