Dijkstra单源最短路径算法

Posted 2021-06-29 博主QQ2449341593

目录

 

一、算法原理

 

一、算法原理

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。
以下图为例，首先介绍Dijstra的原理。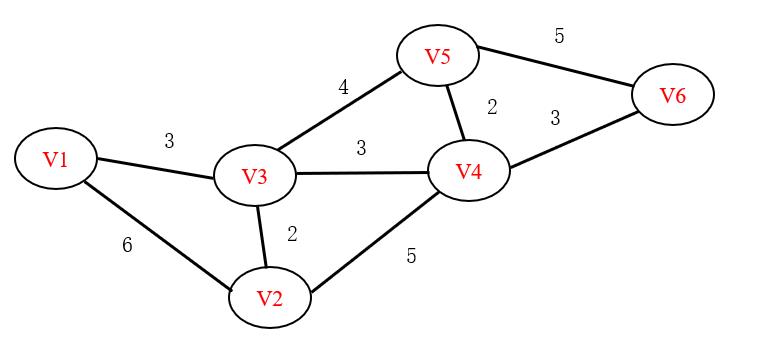

红字为各结点的编号，黑字为各结点之间的距离。

 

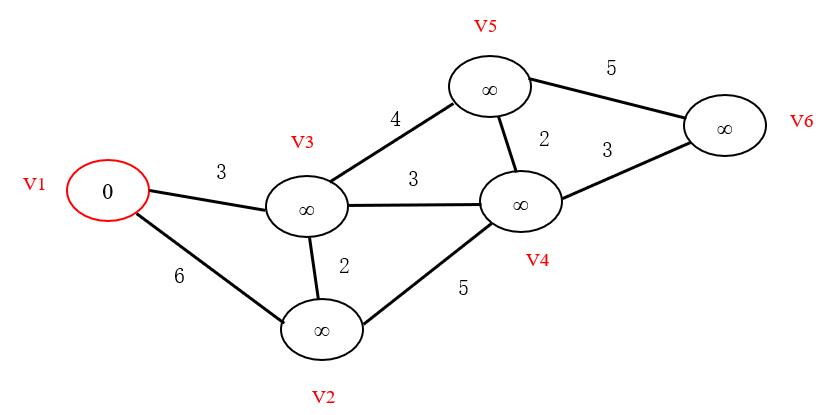
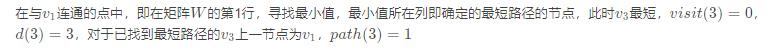
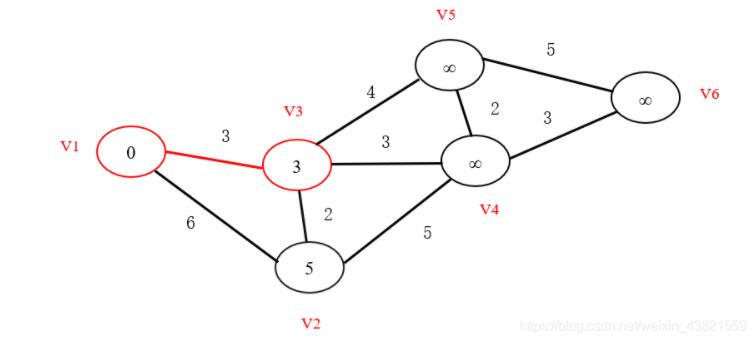
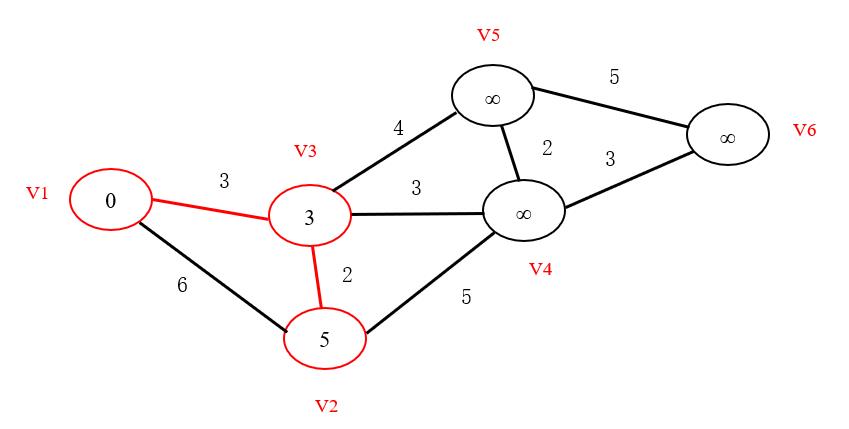
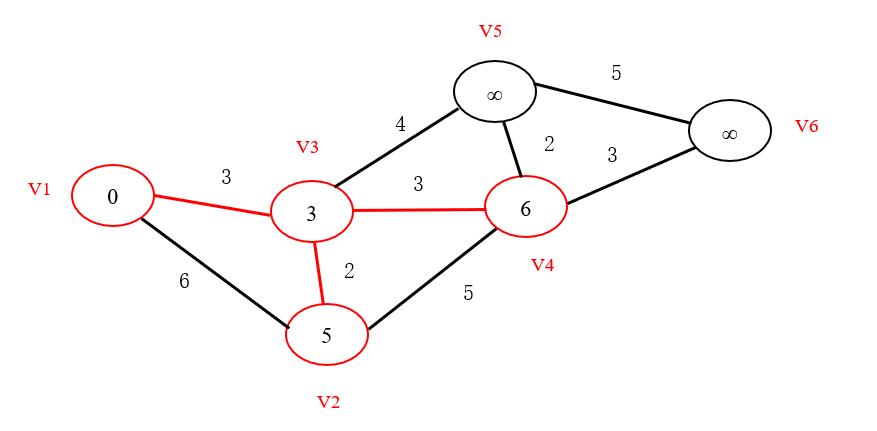
1. 我们可以发现，所要寻找的最短路径即为对于已找到最短路径的点（包括初始结点），在与其连通的，未找到最短路径的结点中，将之间距离与圆圈中的距离（即上一结点已找到的最短路径）相加，求得的最小值。 如果有多个相同的最短距离，任取其中一个。 最终最短路径和距离如下图所示。
   

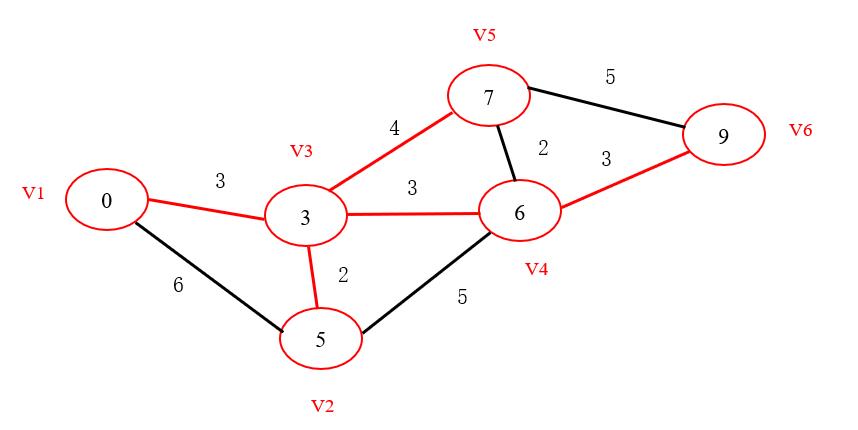
二、MATLAB实现

dijkstra函数如下：

function [distance, path] = dijkstra(W, st, e)
%% dijkstra单源最短路径算法
% 输入：W  权值矩阵   st 搜索的起点   e 搜索的终点
% 输出：distance 路径距离  path  最短路径
n = length(W);          % 节点数
D = W(st, :);
visit = ones(1, n);
visit(st) = 0;          % 已访问  0；未访问  1
parent = zeros(1, n);   % 记录每个节点的上一个节点
path = [ ];
for i = 1:n-1
    temp = [ ];  
    % 从起点出发，找最短距离的下一个点，每次不会重复原来的轨迹，设置visit判断节点是否访问
    for j = 1:n
        if visit(j)
            temp = [temp, D(j)];
        else
            temp = [temp, inf];
        end
    end
    [value, index] = min(temp);
    visit(index) = 0; 
    % 更新：如果经过index节点，从起点到每个节点的路径长度更小，则更新，记录前驱节点，方便后面回溯循迹
    for k = 1:n
        if D(k) > D(index)+W(index, k)
            D(k) = D(index)+W(index, k);
            parent(k) = index;
        end
    end
end
distance = D(e);             % 最短距离
% 回溯法：从尾部往前寻找搜索路径
t = e;
while t ~= st && t > 0
    path =[t, path];
    p = parent(t);
    t = p;
end
path = [st, path];           % 最短路径

测试用例代码如下：

clear;clc;
% 权值表
W = [0 6 3 inf inf inf;
    6 0 2 5 inf inf;
    3 2 0 3 4 inf;
    inf 5 3 0 2 3;
    inf inf 4 2 0 5;
    inf inf inf 3 5 0];
[distance, path] = dijkstra(W, 1, 4)

Command Window中显示的结果为：

distance =

     6


path =

     1     3     4

三、参考文献

[1] 小东和小凤. 最短路径Dijkstra算法原理及Matlab实现. CSDN博客.
[2] 郝搞笑. 详解 Dijkstra算法以及实现. CSDN博客.