单源最短路径Dijkstra算法
Posted 算法入门
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了单源最短路径Dijkstra算法相关的知识,希望对你有一定的参考价值。
一、前言
Dijkstra算法又称单源最短路径算法,顾名思义此算法限定了只有一个源点。这种算法就不适用于求任意两点的最短路径。同时,Dijkstra算法只能处理不存在负权回路的图,这点会在下面细讲。
二、概念
这里我们讲解最短路径,需要掌握几个基本的概念:
对于有向图G=(V,E),权值函数W: E→R(即每条边的权值都为一个实数)
1、路径
p:v1->v2->v3->...vk
表示从v1到vk的一条路径
2、最短路径:
从u到v的一条路径,使w(p)最小,w(p)。
3、最短路径权值:
注意,最短路径可能不存在
(1)当图中存在负权回路,例如: 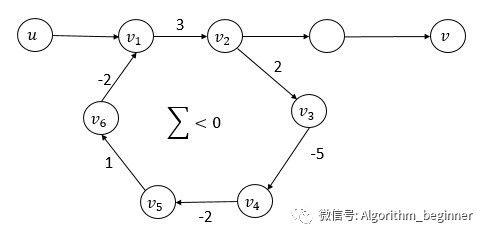
可以看出,存在v1到v6的负权回路,它的权值为-3,如果我们想找从u到v的最短路径,那么无限循环地走这个负权回路可以使最短路径越来越小,最后达到负无穷,那么就说明找不到从u到v的最短路径。
(2)不存在从u到v的路径,这个是肯定不会存在最短路径的。
三、最优子结构
求解源点到某一顶点的最短路径,其实不比求解源点到所有顶点的路径简单。这个时候我们要引入全局的概念,能不能找出所有的顶点的最短路径,然后再去查看到目标点的最短路径呢?很多人就会想到动态规划这一思想,说道动态规划,自然我们首先要考虑的问题是最优子结构。
最短路径满足最优子结构性质:最短路径的子路径是最短路径。 
前提:u到v是最短路径。
证明:(剪贴法)
假设:x到y不是最短路径,那么存在一条更短的路径从x到y(假设为下面的弯箭头),这样,删去原路径中从x到y的路径,用新找到的路径替代(弯箭头),那么就得到了一条比u到v的权值更短的路径,这与前提u到v是最短路径相矛盾,因而x到y是最短路径,即最短路径满足最优子结构性质。
引入三角不等式的概念:(从u到v的最短路径权值,小于等于从u到x的最短路径权值加上从x到v的最短路径权值) 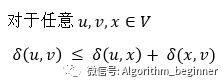
这个性质根据最优子结构性质而来,非常重要。
四、Dijkstra算法思想
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将 加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
五、简单例子说明
初始情况: 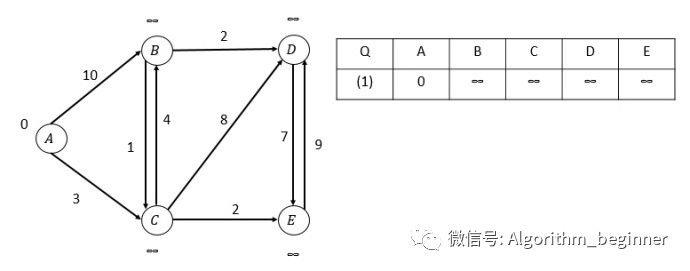
第一次松弛,选取A顶点: 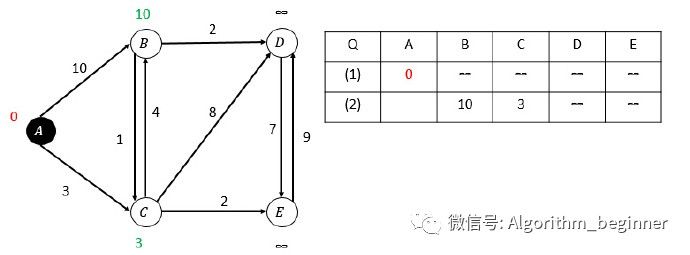
第二次松弛,C的估算距离最小,选取C顶点: 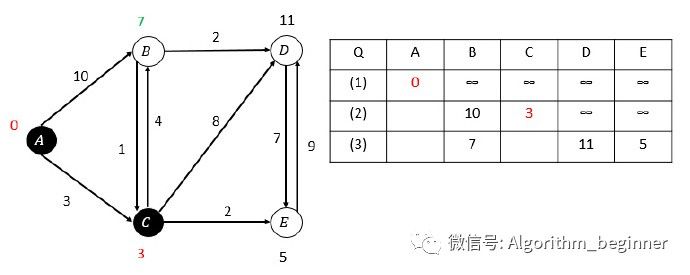
第三次松弛,E的估算距离最小,选取E: 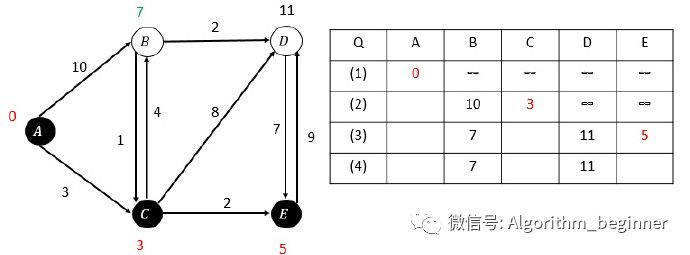
第四次松弛,B的估算距离最小,选取B: 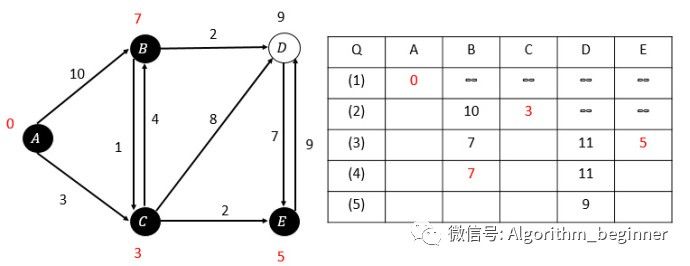
第五次松弛:(最后一个点,完成)
经过所有的松弛操作之后,我们就得到了所有顶点的最短路径(表格中红字部分)。
举个例子
HDU2544
在每年的校赛里,所有进入决赛的同学都会获得一件很漂亮的t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候,却是非常累的!所以现在他们想要寻找最短的从商店到赛场的路线,你可以帮助他们吗?
输入包括多组数据。每组数据第一行是两个整数N、M(N<=100,M<=10000),N表示成都的大街上有几个路口,标号为1的路口是商店所在地,标号为N的路口是赛场所在地,M则表示在成都有几条路。N=M=0表示输入结束。接下来M行,每行包括3个整数A,B,C(1<=A,B<=N,1<=C<=1000),表示在路口A与路口B之间有一条路,我们的工作人员需要C分钟的时间走过这条路。 输入保证至少存在1条商店到赛场的路线。
对于每组输入,输出一行,表示工作人员从商店走到赛场的最短时间
input:
2 1
1 2 3
3 3
1 2 5
2 3 5
3 1 2
0 0
output:
3
2
思路:直接Dijkstra
Dijkstra算法和prime算法的代码差不多,就多了lowcost[k];
代码数据结构用邻接矩阵实现,当然还可以用邻接表实现,,优先队列优化
次版本时间复杂度O(N^2)
int edge[110][110];
int lowcost[110];
int vis[110];
int n,m;
void Dj(int cur)
{
cle(vis);
vis[cur]=1;
for(int i=1;i<=n;i++)
lowcost[i]=edge[cur][i];
int k,Min;
while(1)
{
Min=INF;
for(int j=1;j<=n;j++)
if(!vis[j]&&Min>lowcost[j])
{
Min=lowcost[j];k=j;
}
if(Min==INF)break;
vis[k]=1;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&lowcost[j]>lowcost[k]+edge[k][j])
lowcost[j]=lowcost[k]+edge[k][j];
}
}
cout<<lowcost[n]<<endl;
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
int a,b,c;
while(cin>>n>>m)
{
if(n==0&&m==0)break;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{ if(i==j){edge[i][j]=0;edge[j][i]=0;}
else {edge[i][j]=INF;edge[j][i]=INF;}
}
for(int i=1;i<=m;i++)
{
cin>>a>>b>>c;
if(c<INF)
{ edge[a][b]=c;
edge[b][a]=c;
}
}
Dj(1);
}
return 0;
}
//年轻的代码
欢迎关注:)
以上是关于单源最短路径Dijkstra算法的主要内容,如果未能解决你的问题,请参考以下文章