机器学习梯度消失和梯度爆炸的原因分析表现及解决方案

Posted 2021-06-27 Better Bench

目录

• 1 基本概念
• 2 原因分析
• • 2.1 直接原因
  • 2.2 根本原因
• 3 表现
• 4 解决方案

1 基本概念

（1）梯度不稳定
在深度神经网络中的梯度是不稳定的，在靠近输入层的隐藏层中或会消失，或会爆炸。这种不稳定性才是深度神经网络中基于梯度学习的根本问题。
产生梯度不稳定的根本原因是前面层上的梯度是来自后面层上梯度的乘积。当存在过多的层时，就会出现梯度不稳定场景，比如梯度消失和梯度爆炸。所以梯度消失和梯度爆炸属于梯度不稳定的范畴。
（2）梯度消失和梯度爆炸
BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，计算梯度包含了是对激活函数进行求导，如果此部分大于1，那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸，如果此部分小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减，即发生了梯度消失。
都表现为当前面隐藏层的学习速率低于后面隐藏层的学习速率，即随着隐藏层数目的增加，分类准确率反而下降了。

2 原因分析

2.1 直接原因

（1）梯度消失

• 隐藏层的层数过多
• 采用了不合适的激活函数(更容易产生梯度消失，但是也有可能产生梯度爆炸)

（2）梯度爆炸

• 隐藏层的层数过多
• 权重的初始化值过大

2.2 根本原因

（1）隐藏层的层数过多
从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。因此，梯度消失、爆炸，其根本原因在于在于反向传播算法的不足。
多个隐藏层的网络可能比单个隐藏层的更新速度慢了几个个数量级
（2）激活函数
BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，计算梯度包含了是对激活函数进行求导，如果此部分大于1，那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸，如果此部分小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减，即发生了梯度消失。
sigmoid激活函数和tanh激活函数，其导数的图像如下图所示：

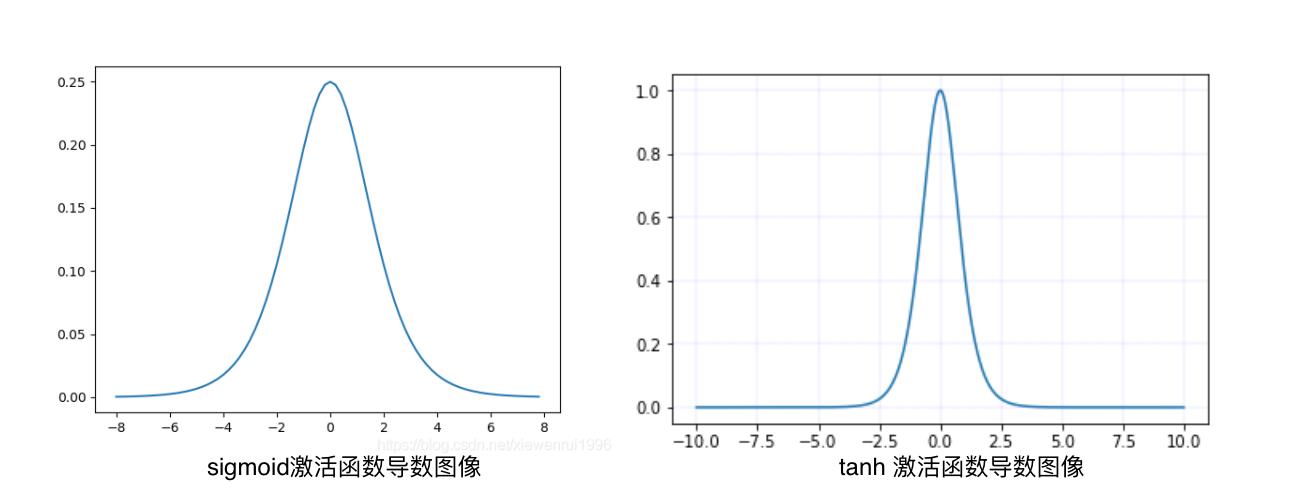
可见左边是sigmoid导数的图像，最大值0.25，如果使用sigmoid作为激活函数，其梯度是不可能超过0.25的，这样经过反向传播的链式求导之后，很容易发生梯度消失。所以说，sigmoid函数一般不适合用于神经网络中。
同理，tanh作为激活函数，它的导数如右图，可以看出，tanh比sigmoid要好一些，但是它的导数仍然是小于1的。也可能会发生梯度消失问题。
（3）初始权重过大
当网络初始权重比较大的情况下，当反向传播的链式相乘时，前面的网络层比后面的网络层梯度变化更快，最终的求出的梯度更新将以指数形式增加，将会导致梯度爆炸。所以，在一般的神经网络中，权重的初始化一般都利用高斯分布(正态分布)随机产生权重值。

3 表现

（1）梯度消失的表现：

• 模型无法从训练数据中获得更新，损失几乎保持不变

（2）梯度爆炸的表现：

• 模型型不稳定，更新过程中的损失出现显著变化
• 训练过程中，模型损失变成 NaN

4 解决方案

梯度消失和梯度爆炸问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题，可以考虑一下以下方案解决：
（1）用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等替代sigmoid函数。
思想也很简单，如果激活函数的导数为1，那么就不存在梯度消失爆炸的问题了，每层的网络都可以得到相同的更新速度。
（2）用Batch Normalization。
那么反向传播过程中权重的大小影响了梯度消失和爆炸，BN就是通过对每一层的输出规范为均值和方差一致的方法，消除了 权重带来的放大缩小的影响，进而解决梯度消失和爆炸的问题，或者可以理解为BN将输出从饱和区拉到了非饱和区(比如Sigmoid函数)。
（3）LSTM的结构设计也可以改善RNN中的梯度消失问题。
在RNN网络结构中，由于使用Logistic或者Tanh函数，所以很容易导致梯度消失的问题，即在相隔很远的时刻时，前者对后者的影响几乎不存在了，LSTM的机制正是为了解决这种长期依赖问题。
（4）ResNet残差网络
相比较以往的网络结构只是简单的堆叠，残差中有很多跨层连接结构，这样的结构在反向传播时具有很大的好处。
（5）预训练加微调
此方法来自Hinton在2006年发表的一篇论文，Hinton为了解决梯度的问题，提出采取无监督逐层训练方法，其基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，此过程是逐层预训练；
在预训练完成后，再对整个网络进行“微调”（fine-tunning）。此思想相当于是先寻找局部最优，然后整合起来寻找全局最优。
（6）梯度剪切
梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
（7）权重正则化
权重正则化（weithts regularization）是一种解决梯度爆炸的方式。正则化是通过对网络权重做正则限制过拟合，仔细看正则项在损失函数的形式：
$$Loss=(y-W^{T}x{)}^2+\alpha ||W(x)|{|}^2$$
其中， $\alpha$是指正则项系数，因此，如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。