Pytorch Note14 激活函数(Activation Function)

Posted 2021-06-27 Real&Love

Pytorch Note14 激活函数(Activation Function)

文章目录

• Pytorch Note14 激活函数(Activation Function)
• 激活函数(Activation Function)
• • Sigmoid
  • tanh
  • ReLU
  • Leaky ReLU
  • ELU
  • Maxout
• Conclusion

全部笔记的汇总贴：Pytorch Note 快乐星球

激活函数(Activation Function)

在之前，我们使用Logistics回归的时候，其中一层就是用了Sigmoid激活函数，可以看到激活函数还是占据了比较重要的地位，下面会介绍一下神经网络中常用的激活函数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ts4Ex8we-1623506929258)(C:\\Users\\86137\\AppData\\Roaming\\Typora\\typora-user-images\\image-20210612212458420.png)]

Sigmoid

Sigmoid 非线性激活函数的数学表达式是$\sigma (x)=\frac{1}{1+e^{-x}}$。我们知道Sigmoid i散活函数是将一个实数输入转化至u 0 ~ 1 之间的输出， 具体来说也就是将越大的负数转化到越靠近0 ，越大的正数转化到越靠近l 9 历史上Sigmoid 函数频繁地使用，因为其具有良好的解释性。

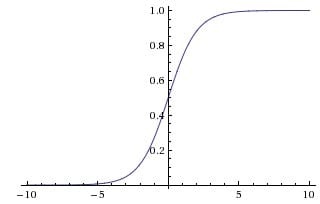
但是最近几年， Sigmoid 激活函数已经越来越少地被人使用了，主要是因为Sigmoid函数有以下两大缺点

1. Sigmoid 函数会造成梯度消失兰一个非常不好的特点就是Sigmoid 函数在靠近1 和 0 的两端时，梯度会几乎变成 0 ，我们前面讲过梯度下降法通过梯度乘上学习率来更新参数，因此如果梯度接近 0 ，那么没有任何信息来更新参数，这样就会造成模型不收敛。 另外，如果使用Sigmoid 函数，那么需要在初始化权重的时候也必须非常小心。

   如果初始化的时候权重太大，那么经过激活函数也会导致大多数神经元变得饱和，没有办法更新参数。

2. Sigmoid 输出不是以0 为均值，这就会导致经过Sigmoid 激活函数之后的输出，作为后面一层网络的输入的时候是非0 均值的，这个时候如果输入进入下一层神经元的时候全是正的，这就会导致梯度全是正的，那么在更新参数的时候永远都是正梯度。怎么理解呢?比如进入下一层神经元的输入是x，参数是w 和b ， 那么输出就是$f=wx+b$，这个时候$\nabla f(w)=x$,所以如果x是0均值的数据，那么梯度就会有正有负， 但是这个问题并不是太严重，因为一般神经网络在训练的时候都是按batch (批)进行训练的，这个时候可以在一定程度上缓解这个问题，所以说虽然0 均值这个问题会产生一些不好的影响，但是总体来讲跟上一个缺点:梯度消失相比还是要好很多。

Conclusion

• Saturated neurons “kill” the gradients
• Sigmoid outputs are not zero centered
• exp() is a bit compute expensive

tanh

Tanh 激活函数是上面Sigmoid 激活函数的变形，其数学表达为$tanh(x)=2\sigma (2x)-1$

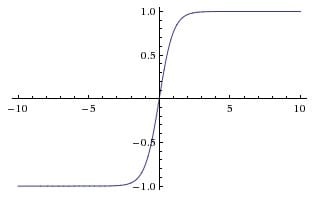
它将输入的数据转化到 -1 ~ 1 之间，可以通过图像看出它将输出变成了 0 均值，在一定程度上解决了Sigmoid 函数的第二个问题，但是它仍然存在梯度消失的问题。因此实际上Tanh 激活用数总是比Sigmoid 激活函数更好。

Conclusion

• Squashes numbers to range [-1,1]
• zero centered (nice)
• still kills gradients when saturated

ReLU

ReLU 激活函数( Rectified Linear Unit )近几年变得越来越流行，它的数学表达式为$ReLU(x)=max(0,x)$，，换句话说，这个激活函数只是简单地将大于 0 的部分保留，将小于 0 的部分变成0

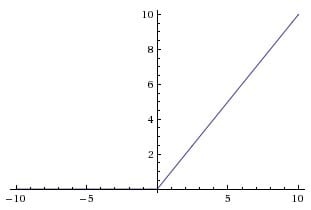
ReLU 的优点:

1. 相比于Sigmoid 激活函数和Tanh 激活函数， ReLU 激活函数能够极大地加速随机梯度下降法的收敛速度，这因为它是线性的，且不存在梯度消失的问题。
2. 相比于Sigmoid 激活民l数和Tanh 激活函数的复杂计算而言， ReLU 的计算方法更加简单.只需要一个闽值过滤就可以得到结果，不需要进行一大堆复杂的运算。

ReLU 的缺点:

• 训练的时候很脆弱，比如一个很大的楠度经过ReLU 激活函数，更新参数之后，会使得这个神经元不会对任何数据有激活现象。如果发生这种情况之后，经过ReLU 的梯度永远都会是0 ，也就意味着参数无法再更新了，因为ReLU 激活函数本质上是一个不可逆的过程，因为它会直接去掉输入小于 0 的部分。在实际操作中可以通过设置比较小的学习率来避免这个小问题。

Conclusion

DisAdvantage

• Does not saturate (in +region)
• Very computationally efficient
• Converges much faster than sigmoid/tanh in practice

Advantage

• Not zero-centered output

• ReLU units can “die”

Leaky ReLU

Leaky ReLU 激活函数是ReLU 激活函数的变式，主要是为了修复ReLU 激活函数中训练比较脆弱的这个缺点.不将x < 0 的部分变成 0 ，而给它一个很小的负的斜率，比如0.01 ，它的数学形式可以表现为$f(x)=I(x<0)(\alpha x)+I(x\ge 0)(x)$，其中$\alpha$一个很小的常数，这样就可以使得输入小于0的时候也有一个很想小的梯度。

关于LeakyReLU 激活函数的效果，众说纷纭， 一些实验证明很好，些实验证明并不好。

同时也有人提出可以对α 进行参数化处理，也就是说可以在网络的训练过程巾对α 也进行更新，但是再对所有情况都有效，目前也不清楚。
$$f(x)=max(0.01x,x)$$

Conclusion

• Does not saturate
• Computationally efficient
• Converges much faster than sigmoid/tanh in practice! (e.g. 6x)
• will not “die”.

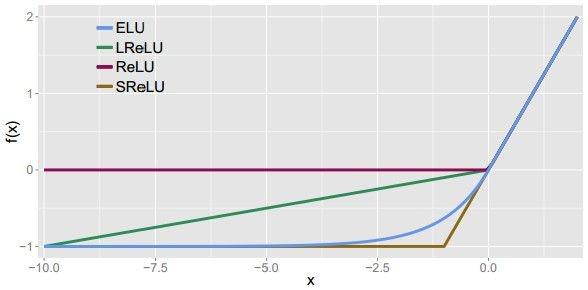
ELU

ELU函数是针对ReLU函数的一个改进型，相比于ReLU函数，在输入为负数的情况下，是有一定的输出的，而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题，不过还是有梯度饱和和指数运算的问题。

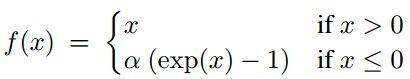
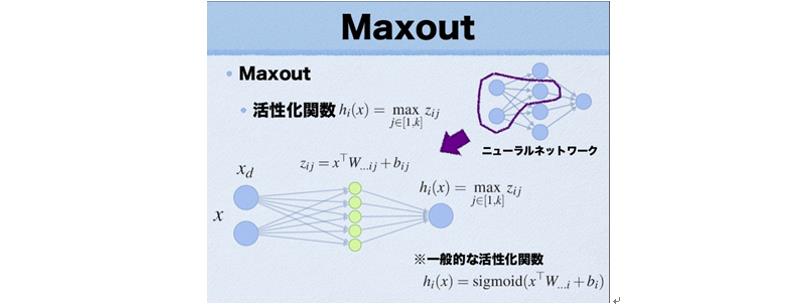
Maxout

另外一种激活函数的类型并不是f( wx + b) 作用在一种输山结果的形式，而是$max(w_{1}x十b_1，w_{2}x十b_2)$这种Maxout 的类型，可以发现ReLU 激活函数只是Maxout中ω1 = 0, b1 = 0 的特殊形式。因此Maxout 既有着ReLU 激活函数的优点，同时也避免了ReLU 激活函数训练脆弱的缺点。不过，它也有一个缺点，那就是它加倍了模型的参数，导致了模型的存储变大。

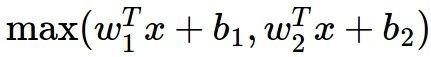
Conclusion

• Use ReLU. Be careful with your learning rates 如果要用ReLU，要注意学习率
• Try out Leaky ReLU / Maxout / ELU 尝试用Leaky ReLU / Maxout / ELU
• Try out tanh but don’t expect much 尝试用tanh但不要期望太大
• Don’t use sigmoid 不要用sigmoid

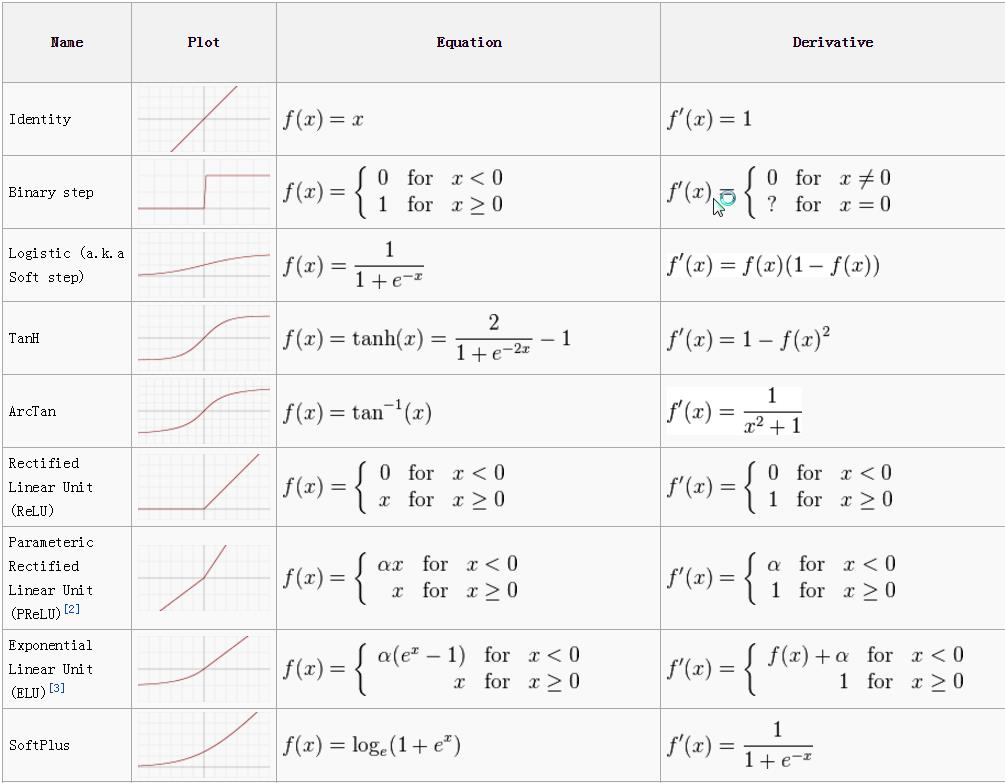
我们可以看一下许多激活函数

下一章传送门：Note15 优化算法1 梯度下降（Gradient descent varients）