Python描述数据结构之最短路径篇
Posted 夏小悠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python描述数据结构之最短路径篇相关的知识,希望对你有一定的参考价值。
前言
本篇章主要介绍图的最短路径问题,包括Dijkstra算法和Floyd算法,并用Python代码实现。
1. 创建图
在开始之前,我们先创建一个图,使用邻接矩阵表示有向网:
class Graph(object):
"""
以邻接矩阵为存储结构创建有向网
"""
def __init__(self, kind):
# 图的类型: 无向图, 有向图, 无向网, 有向网
# kind: Undigraph, Digraph, Undinetwork, Dinetwork,
self.kind = kind
# 顶点表
self.vertexs = []
# 边表, 即邻接矩阵, 是个二维的
self.arcs = []
# 当前顶点数
self.vexnum = 0
# 当前边(弧)数
self.arcnum = 0
def CreateGraph(self, vertex_list, edge_list):
"""
创建图
:param vertex_list: 顶点列表
:param edge_list: 边列表
:return:
"""
self.vexnum = len(vertex_list)
self.arcnum = len(edge_list)
for vertex in vertex_list:
vertex = Vertex(vertex)
# 顶点列表
self.vertexs.append(vertex)
# 邻接矩阵, 初始化为无穷
self.arcs.append([float('inf')] * self.vexnum)
for edge in edge_list:
ivertex = self.LocateVertex(edge[0])
jvertex = self.LocateVertex(edge[1])
weight = edge[2]
self.InsertArc(ivertex, jvertex, weight)
def LocateVertex(self, vertex):
"""
定位顶点在邻接表中的位置
:param vertex:
:return:
"""
index = 0
while index < self.vexnum:
if self.vertexs[index].data == vertex:
return index
else:
index += 1
def InsertArc(self, ivertex, jvertex, weight):
"""
创建邻接矩阵
:param ivertex:
:param jvertex:
:param weight:
:return:
"""
if self.kind == 'Dinetwork':
self.arcs[ivertex][jvertex] = weight
有关邻接矩阵中顶点结点
Vertex()的定义可以参考这篇博客,这里就不在贴出相应的代码了。
2. 问题来源
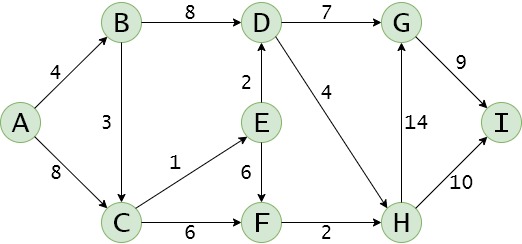
假如我从城市
A
A
A出发坐火车去其他城市旅游,那么如何规划路线使所花费的车票钱最少呢?若将上述图中的城市看成有向网中的顶点,并将两城市之间所需要的车票钱看做对应弧的权值,那么这一问题的本质就是求两个顶点之间权值最小的路径,简称最短路径
(
S
h
o
r
t
e
s
t
(Shortest
(Shortest
P
a
t
h
)
Path)
Path)。
3. Dijkstra算法
D
i
j
k
s
t
r
a
Dijkstra
Dijkstra算法,中文名叫迪杰斯特拉算法,它常用于求解源点到其余顶点的最短路径。
假设
G
=
{
V
,
{
A
}
}
G=\\{V, \\{A\\}\\}
G={V,{A}}是含有
n
n
n个顶点的有向网,以该图中的顶点
v
v
v为源点,使用
D
i
j
k
s
t
r
a
Dijkstra
Dijkstra算法求顶点
v
v
v到图中其余各顶点的最短路径的基本思路如下:
(1) 使用集合
S
S
S记录已求得最短路径的终点,初始时
S
=
{
v
}
S=\\{v\\}
S={v};
(2) 选择一条长度最短的路径,该路径的终点
w
∈
V
−
S
w\\in V-S
w∈V−S,将
w
w
w并入
S
S
S,并将该最短路径的长度记为
D
w
D_w
Dw;
(3) 对于
V
−
S
V-S
V−S中任一顶点
s
s
s,将源点到顶点
s
s
s的最短路径长度记为
D
s
D_s
Ds,并将顶点
w
w
w到顶点
s
s
s的弧的权值记为
D
w
s
D_{ws}
Dws,若
D
w
+
D
w
s
<
D
s
D_w+D_{ws}<D_s
Dw+Dws<Ds,则将源点到顶点
s
s
s的最短路径的长度修改为
D
w
+
D
w
s
D_w+D_{ws}
Dw+Dws;
(4) 重复执行上述操作,直到
S
=
V
S=V
S=V。
D
i
j
k
s
t
r
a
Dijkstra
Dijkstra算法有些
P
r
i
m
Prim
Prim算法的影子,这里使用一个辅助列表Dist,用来存储源点到每一个终点的最短路径长度,列表Path来存储每一条最短路径中倒数第二个顶点的下标(弧尾下标),除此之外还需要一个列表flag来记录顶点是否已求得最短路径。下面结合着
D
i
j
k
s
t
r
a
Dijkstra
Dijkstra算法来分析一下上面的那个有向网:
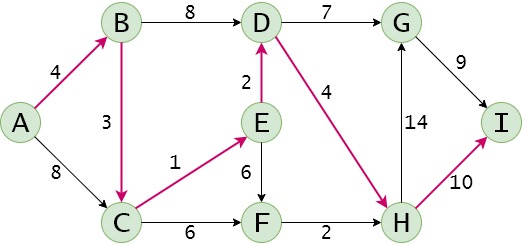
(1) 这里要做的就是更新列表 以上是关于Python描述数据结构之最短路径篇的主要内容,如果未能解决你的问题,请参考以下文章Dist和列表Path,假如以顶点
A
A
A为起始点,先将它加入
S
S
S中,然后寻找以顶点
A
A
A为弧尾的最短路径,这里找到了顶点
B
B
B,然后继续找下一个顶点。这个时候就要做一个判断了,即
D
w
+
D
w
s
<
D
s
D_w+D_{ws}<D_s
Dw+Dws<Ds是否成立,这里的顶点
s
s
s有两种选择,要么是顶点
C
C
C,要么是顶点
D
D
D,因为这两个顶点都是以顶点
w
w
w(即顶点
B
B
B)为弧尾,按照顺序,这个时候先选择了顶点
C
C
C,经判断:
D
A
B
+
D
B
C
<
D
A
C
D_{AB}+D_{BC}<D_{AC}
DAB+DBC<DAC(即
4
+
3
=
7
<
8
4+3=7<8
4+3=7<8)成立,然后更新源点到顶点
s
s
s(即顶点
C
C
C)的距离为7。这个时候顶点
s
s
s又选择了顶点
D
D
D,经判断:
D
A
B
+
D
B
D
<
D
A
D
D_{AB}+D_{BD}<D_{AD}
DAB+DBD<DAD(即
4
+
8
=
12
<
∞
4+8=12<\\infty
4+8=12<∞)成立,然后更新源点到顶点
s
s
s(即顶点
D
D
D)的距离为12。
(2) 然后寻找以顶点
C
C
C为弧尾的最短路径,这里找到了顶点
E
E
E,然后做一个路径长度判断,经判断:
D
A
C
+
D
C
E
<
D
A
E
D_{AC}+D_{CE}<D_{AE}
DAC+DCE<DAE(即
7
+
1
=
8
<
∞
7+1=8<\\infty
7+1=8<∞)成立,然后更新源点到顶点
s
s
s(即顶点
E
E
E)的距离为8,然后又找到了顶点
F
F
F,然后做一个路径长度判断,经判断:
D
A
C
+
D
C
F
<
D
A
F
D_{AC}+D_{CF}<D_{AF}
DAC+DCF<DAF(即
7
+
6
=
13
<