2021 泰迪杯 A 题

Posted 2021-06-26 zhuo木鸟

泰迪杯 A 题

• 思路
• 数据读取
• 分析数据
• • 数据类型和缺失值
  • 缺失值处理（FLAG 除外）
  • 画图与统计描述
  • • 计算各列的统计信息
    • 转换数据集（省内存走起）
    • 画图
    • • KDE 图
      • 频率柱状图
• 数据预处理
• • 对 int、类别（category） 类型的数据，查看其取值个数：
  • 报告截止日期 vs 截止日期？——单位是天吗？
• 第一问（以‘制造业’为例）
• • 给数据加上行业标签
  • 离群数据处理
  • 标准化处理
  • 筛选指标
  • • 根据偏相关系数进行筛选
    • 配合 FLAG 筛选
    • • 原始数据？
      • 不变？显著大于？
      • 机器学习模型？
      • 特征权重？
      • 结果
• 第一问最终结果
• • 过程
  • 结果
• 第二问
• • 时序性？
  • 机器学习方法解决
  • • 筛选最佳参数
    • 筛选最佳算法
    • 效果评价 + 挑出第6年数据造假的企业（股票编号）
  • 深度学习方法
  • • 筛选网络拓扑
    • 结果输出
• 第三问
• • 可以筛选出指标、且数据充足的行业，造假判断结果：
  • 数据不足，无法筛选指标的行业，造假预测结果：
  • • 标准化+聚类
    • • Kmeans 聚类 + 折臂图
    • 筛选影响指标
    • 机器学习方法
    • 意外
• 代码与提问
• 附件
• • IQR 诊断法
  • 偏相关系数
  • 类别不均衡问题
  • • 单边选择
    • ADASYN
  • 交叉验证
  • 网格寻优
  • KMeans 聚类

---

本人专挑数据挖掘、机器学习和 NLP 类型的题目做，有兴趣也可以逛逛我的数据挖掘竞赛专栏。

本人不会回访，不互关，不互吹，以及谢绝诸如此类事

赛题官网：https://www.tipdm.org/

思路

https://blog.csdn.net/weixin_42141390/article/details/116423465

返回目录

数据读取

原本这里采用 dask 库读取 csv 文件。因为 dask 库的好处是：1、分块；2、并行化计算

然而：我先尝试了用 pandas 读取数据，读入整个 CSV 占用内存 76 MB。算是比较小的了。鉴于其可直接放入内存之中，因此就不需要分块了，因为反而会因为与硬盘交互，消耗 CPU 资源。

经过测试，用 dask 读取数据，虽然可以分块，但需要启动并行化客户端，所以占用内存共 490 MB，而用 pandas 读取，仅占用了 230 MB，因此，选择 pandas 库。

%%time
df = dd.read_csv(r'../泰迪杯/泰迪杯 A 题/附件/附件2.csv')
df    # 可视化头五行数据

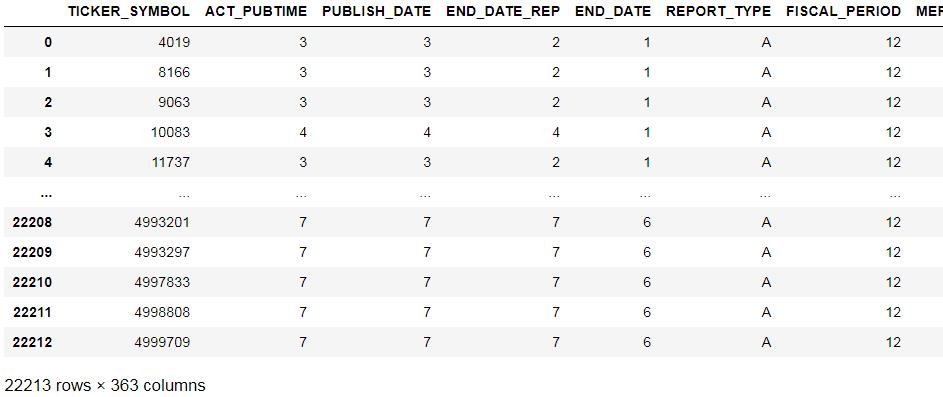
（补：本人读取完数据后，CPU 已经占用 78% 了… 惭愧）

返回目录

分析数据

数据类型和缺失值

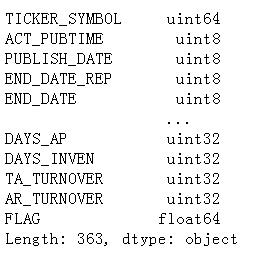
print(df.dtypes)    # 查看各行的类型

各列的类型如下所示：

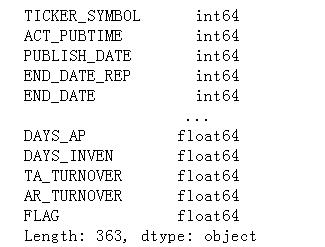
为何要没事找事，打印出数据类型呢？为了节省内存呀…，这里先按下不表。

再看数据各列的缺失值数量如何：

print(df.isna().sum())    #缺失值计算 

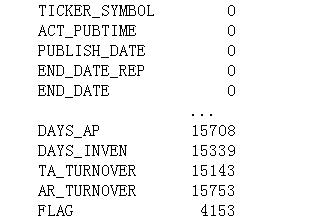
经过详细分析，可以看到附件二还是挺良心的。那些类型为 int 的数据，没有缺失值，但一些类型为 float 的数据，就有较多的缺失值了。如下图所示，下面给出的这些列，类型都是 int 或者 category，他们都没有缺失值：

再看， FLAG（有无造假标签）居然也有缺失值。结合题目，那些 FLAG 带有缺失值的， 应该是需要我们在第二题、第三题中求解的 。所以，在数据预处理完毕后，我们还需要对表格，根据有无 FLAG 进行拆分。

先来看一下有多少数据没有 FLAG 吧：

可以看到，有 4153 条数据是没有 FLAG 的。

返回目录

缺失值处理（FLAG 除外）

由于那些数据类型为字符串（object）的列不包括缺失值，因此，用 0 代替缺失值，不会造成过大影响。且用 0 代替，能与现有的数据情况相匹配，本人曾将数据转为 excel 表格，并从中发现，有些数据虽然没有缺失值，但却用 0 去代替了，如下图所示：

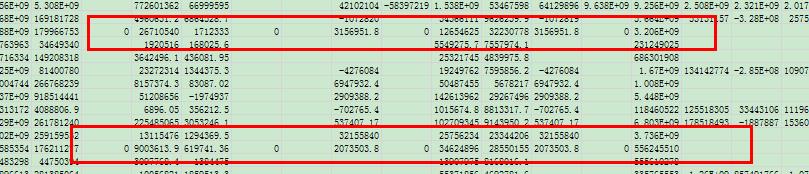
所以，这里也用 0 去替代缺失值。

返回目录

画图与统计描述

计算各列的统计信息

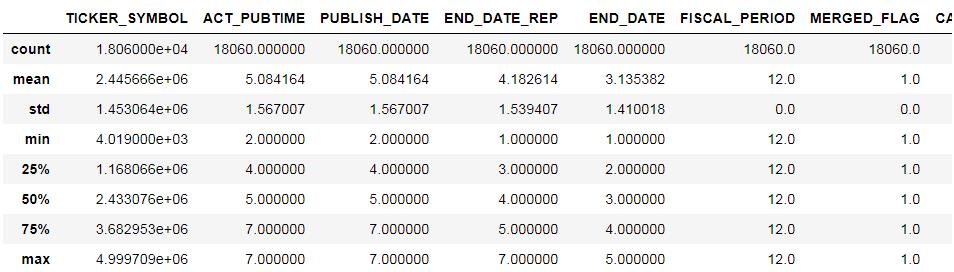
我们从中得出如下信息：

1. 由于股票代码最大编号＞65536，所以在接下来的内存转换中，要用 uint64。
2. 各列的量纲、以及方差都各不相同，需要我们进行标准化

返回目录

转换数据集（省内存走起）

根据各列的类型，我们可以在数据存储上再拉紧裤腰带，我们修改数据集的类型，将那些整数（单位为天、年、次）或者是类别型换成 int8、category 等等：

返回目录

画图

KDE 图

挑选 TFA_TURNOVER 列画出数据的 KDE 图（密度分布图）：

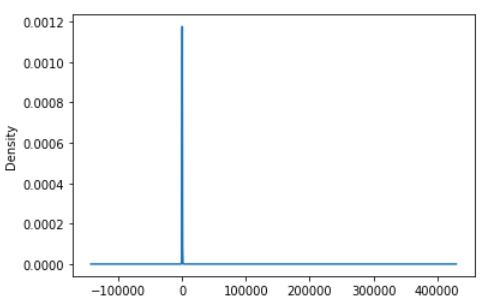
频率柱状图

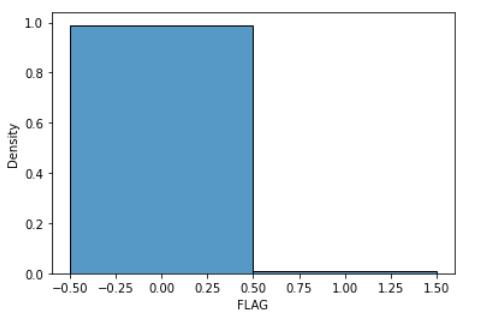
从这张图中可以看出：造假的企业和没有造假的企业，在数量上极度不均衡！

返回目录

数据预处理

对 int、类别（category） 类型的数据，查看其取值个数：

如下：

列 ACT_PUBTIME 即 实际披露时间 的取值个数共6个.
取值为：[3, 4, 2, 5, 6, 7]
列 PUBLISH_DATE 即 发布时间 的取值个数共6个.
取值为：[3, 4, 2, 5, 6, 7]
列 END_DATE_REP 即 报告截止日期 的取值个数共7个.
取值为：[2, 4, 3, 1, 5, 6, 7]
列 END_DATE 即 截止日期 的取值个数共6个.
取值为：[1, 2, 3, 4, 5, 6]
列 REPORT_TYPE 即 报告类型 的取值个数共1个.
取值为：[‘A’]
列 FISCAL_PERIOD 即 会计区间 的取值个数共1个.
取值为：[12]
列 MERGED_FLAG 即 合并标志：1-合并，2-母公司 的取值个数共1个.
取值为：[1]
列 ACCOUTING_STANDARDS 即 会计准则 的取值个数共1个.
取值为：[‘CHAS_2007’]
列 CURRENCY_CD 即 货币代码 的取值个数共1个.
取值为：[‘CNY’]

从这里大家可以看出什么呢？

1. 造假标准肯定和那些取值仅一个的无关，也即可以直接排除：{ 报告类型、会计区间 、合并标志、会计准则、货币代码 }
2. 第二题中的“第六年”，到底指的是：ACT_PUBTIME，还是 PUBLISH_DATE？ 个人觉得应取发布时间。这点大家可以在论文中声明一下。
3. 删除完 { 报告类型、会计区间 、合并标志、会计准则、货币代码 } 后，那些类型为 category 的列就没有了。所以，在后面的操作中，不需要进行 one-hot 编码。

大家也可以按照同样的方法，去判断权益乘数，但其取值有 6000+ 多个呢，所以就别将他转为类别变量了。

然后，大家请思考：那些没被删除的日期数据，他们可以转换为 category 类型吗？ 这个问题还是先挂着，下一节分晓。

这里，我们来看到，发布时间有 2-7 年。那么，是不是每一个企业，都有 2-7 年的数据呢？

这个问题还是比较重要的，最完美的情况是，每一家企业都有 2-7 年的数据。这种情况下，在接下来的分析中，就不得不考虑数据是否有时序性了。换句话说，今年造假，是否和去年的数据有关（即使去年没造假）。

基于这个理由，我们首先来看看，每一个企业是否真的都有2-7年的数据：

df.groupby(by='TICKER_SYMBOL').count()

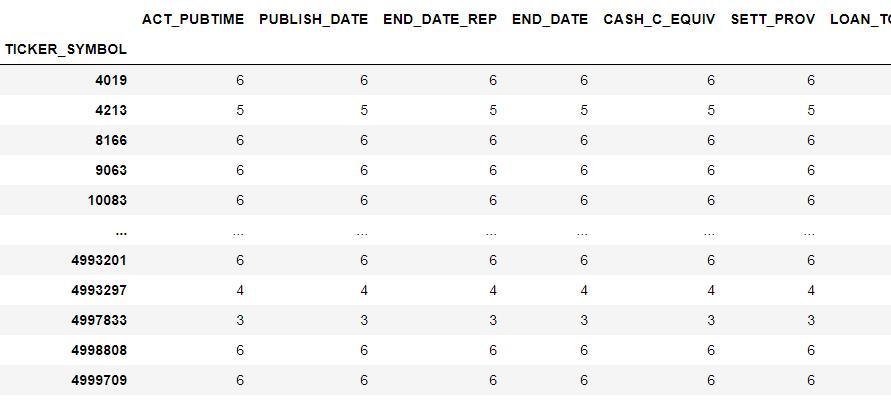很让人瑟瑟发抖的是：大部分的企业都有 6 组数据，$7-2+1=6$。所以，记住这个结论，之后我们解第二问、第三问，都应该要至少提到时序性的问题。

返回目录

报告截止日期 vs 截止日期？——单位是天吗？

报告截止日期与截止日期，咋看之下好像是一样的，但仔细观察可以发现：报告截止日期总是大于截止日期，我们验证一下：

np.any(df.END_DATE_REP > df.END_DATE)

结果为 True ！

换句话说：我们是否可以理解为，截止日期是规定的审计结束日期，而报告截止日期是审计结束之后，审计单位整理报告上报的日期？

如果是这样，那么（报告截止日期-截止日期），即企业拖拉症状，应该与截止日期无关才对，即两者作为随机变量应是相互独立的。于是，我们就可以用列联表的方式，用统计检验的方法，来考察两者的分布是否独立。

若独立，我们就可以将报告截止日期、截止日期，用（报告截止日期-截止日期）（即企业拖拉情况）来替换。因为一个企业拖拉的程度，更能够体现出这个企业造假的态度。

这样子的变换看上去似乎没有太大意义，但要知道，我们的数据只有 2W，而行业大约 20 个，每一个企业还有 300+ 的列数。平均下来，每一列仅有 3 个数据（不严谨的说法），因此数据的密度是非常低的。能够降低列数，不单单可以提高效率，也可以提高准确率！

闲话少说，我们取原假设为：截止日期、（报告截止日期-截止日期）（下面用$\Delta$代替）两个变量相互对立，首先构建用于独立检验的列联表：

df_for_table = df.loc[:,['END_DATE_REP','END_DATE']]
df_for_table['Delta'] = df_for_table.iloc[:,0] - df_for_table.iloc[:,1]
df_for_table = df_for_table.groupby(by=['END_DATE','Delta']).count()
df_for_table

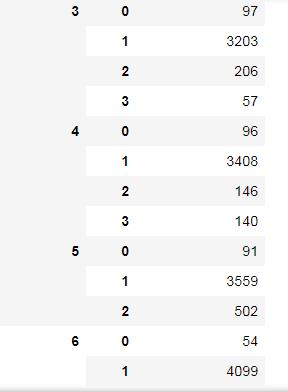
从结果表中，我们可以看出，END_DATE 取 5 和 6 的时候（此时单位我们还不知，可能是天、月、年），$\Delta$ 最大值分别是 2 和 1。即，END_DATE_REP 的最大取值为 7。仔细回忆，我们的发布时间、实际披露时间的最大值也是为 7 。

于是，不难得出，END_DATE 和 END_DATE_REP 的单位是年！

为了分析方便，我们将 END_DATE 为 5 和 6 的删除，并构建列联表：

obs = np.zeros((4,4))
for i in range(4):
    tmp = df_for_table[4*i:4*(i+1)].values.reshape(-1)
    obs[i,:] = tmp
obs

构建好列联表后，进行假设检验，结果如下：
检验统计量的值为 3521.1458225666274
p-值为 0.0

根据假设检验的结果，由于 p值为 0，所以很遗憾，我们需要拒绝原假设，并有100%的把握，可以说拖延时间$\Delta$ 和截止时间是相关的。

不过，为了提高模型的辨识度（数据密度实在太低了），我们可以用 $\Delta$ 去替换 END_DATE_REP。

同上述分析，我们也需要考虑 PUBLISH_DATE 和 ACT_PUBTIME 之间的关系。来判断两者之间，是不是实际发布时间，大于等于发布时间？

np.any(df.ACT_PUBTIME >= df.PUBLISH_DATE)

结果是 True。于是，我们是否也可以列一个发布拖延时间：（实际发布时间-发布时间）。

如果判断出发布拖延时间，与发布时间，作为随机变量是相互独立的。那么，不仅可以为我们省下一列，而且，如果我们不用考虑数据的时序性，至少在做简单分析的时候可以这样。之所以可以不考虑时序性，是因为延迟时间，一定程度上代表了时序性的作用！

话不多说，先搭建一个列联表，结果如下：

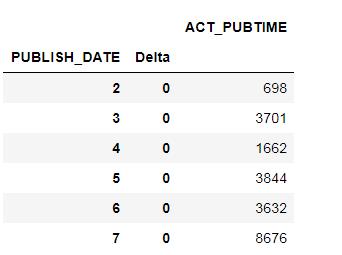
然而，从这个表可以看出，原来所有企业的实际发布时间，和发布时间都是相同的。不过也好，借此机会可以删除 ACT_PUBTIME 列。

同时我们也看到，PUBLISH_DATE 的取值为 2~7，应当是一个索引数据。用 SQL 语言的话说，它和 TICKET_SYMBOL 构成表格的主键。所以，不能将其转为 category 类型，更不用说对他进行 one-hot 编码了。

在接下来的问题中，它和股票代码应是用来识别数据，不参与运算的。同时，它们两个实际上对是否造假所起到的作用和信息量，都包含在其他列里面了。所以，在之后的分析中，这两列不参与分析。

但还是需要考虑，如果忽略了 PUBLISH_DATA（发布时间），那么就等于丢弃了数据的时序性，这样好吗？

对于第一问，我们不考虑时序性。因为我们的指标，是对整个行业来筛选的。若考虑时序性，那么结果只能局限于企业而非行业。

对于第二问和第三问，我们无法考虑时序性，因为我们需要解决类别不均衡问题，后文会谈到。

返回目录

第一问（以‘制造业’为例）

确定数据是否造假的决定指标，本质上是一个数据降维的问题。首先，为了便于数据的处理，首先要对数据进行标准化。

但在标准化前，首先应该考虑：数据标准化需不需要根据行业，采用不同的标准化基础？还是将整个表格直接标准化？答案当然是前者。毕竟，不同行业间，我们很有理由认为量纲各不同。

给数据加上行业标签

首先读取附件1：

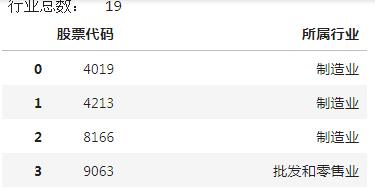
同时可以从附件1 中看出，给出的行业一共有 19 个。

要如何给数据附上标签呢？这就要用到 SQL 里的 join 操作了。但要怎么 join 呢？是左连接、右连接，还是内连接？

由于有些企业没有在附件一中有具体的分类，因此，可能有人再考虑用左连接的自然连接。但你要知道，问题二、问题三都是求其他行业的，所以如果你狠心一点，直接用 inner join（内连接），将那些没有归入行业的企业划掉！！

（本人用内连接）附上标签以后，就要着手标准化数据了。

准化的方式一般有两种：

1. 用最大值、最小值
2. 用均值、方差

由于上述标准化都对离群值敏感，所以首先要排除离群数据：

离群数据处理

离群值数据，当然要以行业为单位考虑。毕竟，有些行业某个列的总体数值偏高，总不能把他们都删了吧。

据分析，这些报表造假也好，详细记录的也好，应该都不会偏离正常值太多。但如果详细记录却出现离群值的，一般是因为数据录入出现错误。此外，造假与否本身也会产生离群值，所以，在离群值识别的时候，我们要制定一个很宽松的标准。
然后，我们将离群数据删除！

这里采用的离群值识别算法是：IQR 方法。若一整行中，若果全部行通过 IQR 诊断为离群值，则删去。

标准化处理

这里采用均值、方差标准化（标准化后均值=0，方差=1）处理。之所以采用这种方法，是因为最大、最小标准化难以体现数据的差异性。

在标准化时，要根据行业分组进行，原因在于，每一个行业可能的量纲不同。

我们把数据拆分成两部分：

1. df_flag ： 指那些带有 FLAG 标签的数据
2. df_noflag：指那些 FLAG 为 NAN 的数据

然后，将 df_flag、df_noflag 按照行业，拆分成 19 个子集（行业共19个嘛）。再对每一个子集进行标准化。

注意，标准化时候，是将 df_flag、df_noflag 一起标准化（同一行业）：
$$x_{ij}^{\prime }=\frac{x_{ij}-\overline{x_i}}{std(x_i)}$$

返回目录

筛选指标

筛选指标其实，就是叫我们进行数据降维，为了方便阐述，以后都会把输入变量称为特征¹。

根据偏相关系数进行筛选

第一问叫我们找决定指标，而我们知道，一些指标（特征）自身相互决定。因此，或多或少带有一定的冗余，所以在进行进一步地筛选之前，我们需要先删除多余的指标。

偏相关系数度量了两个变量，在刨除其他变量后的线性相关特性²。所以，这里计算了指标两两的相关性，构成一个偏相关系数矩阵：

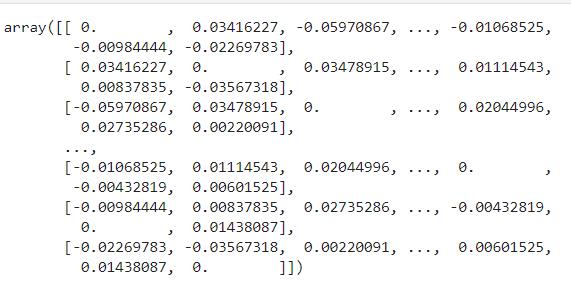
（上述矩阵将自身与自身的相关系数设为 0）然后，再根据相关系数矩阵，遍历所有特征，若两个特征相关性大于 0.8 ，则删除其中一个。

一顿操作下来，数据变成这样（以制造业为例）：

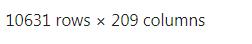
209 列还是加上了 （发布时间、股票代码、所属行业和 FLAG 的），所以最后特征只剩下 205 列，不过这个数字还是比较大的。

返回目录

配合 FLAG 筛选

根据相关性的筛选是一种“窝里斗”的筛选。现在我们要结合 FLAG 来筛选了。

我们要找的是，决定企业是否造假的决定性指标。所以，如果我们搭建一个机器学习模型，而这个机器学习模型根据现有特征，和 FLAG 构成的数据进行训练，然后得出模型的精确度为 $s$。然后再删除一些特征，再重复上一个过程。若模型的精确度不变，则删去特征，直到精确度明显降低为止：

返回目录

原始数据？

在进行机器学习模型训练的时候，由于数据的类别不均衡，所以需要我们通过采样的方法，减少主类别的数量；增加次类别的数量，从而达到主类别、次类别的平衡。

举个例子，假如 1% 的企业造假，99%的企业不造假。那么，一个只会回答 不造假 的模型，就能达到 99% 的精确度…

为了解决这个问题，这里采用单边选择法，先进行欠采样，再用 ADASYN 法进行过采样。最后得出 造假：不造假 = 1:1.

一顿操作下来，数据变成这样（以制造业为例）：

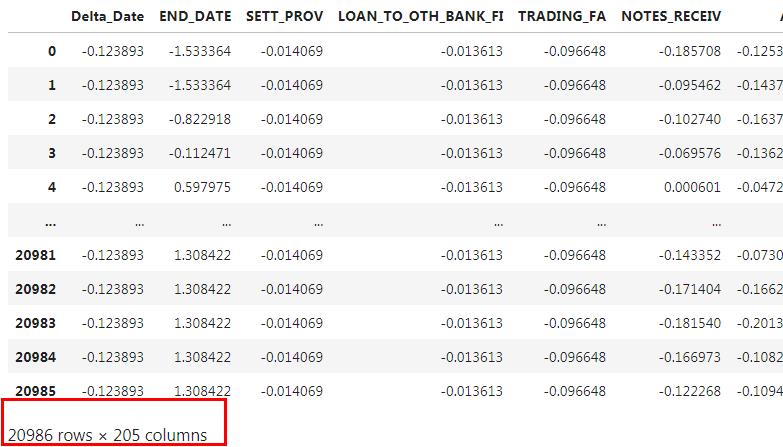
数据量大约翻了一倍

返回目录

不变？显著大于？

若模型的精确度在删除特征前后不变，则保留？那么不变是什么意思呢？我们知道，模型的训练算法的收敛是具有偶然性的。所以每一次训练的结果都不相同，精确度也自然不同，那么怎么才能叫不变呢？

首先，在训练模型，获得精确度的时候，当然不能做一次。这个过程，要重复做 10 次，怎么做呢？交叉验证，最后得到 10 个精确度。删除特征后，再重复一次，再得到 10 个精确度。

然后，将这两组精确度，进行单边 T 检验。原假设为：两组数据的均值不变；备选假设为：删除前精确度的均值 > 删除后。

返回目录

机器学习模型？

用什么机器学习模型呢？应该考虑如下几点：

1. 简单，快速
2. 能进行非线性分类
3. 能评估每一个特征的权重（对结果的重要性）

综上，我觉得可以用决策树、SVC。但是 SVC 在非线性分类方面做得不是很好，且训练比较复杂，所以本文用的决策树。

返回目录

特征权重？

若采用决策树的话，特征权重就可以用每个特征的 Gini 系数来代替了。

若用 SVC 的话，可以考虑使用 SVC 模型的每个特征的系数。

返回目录

结果

以“制造业”为例（强调了3次了），使用上述算法，最后的筛选结果是：

迭代终止，终止原因是：特征只剩一个啦！
筛选过后的数据： [[-1.59929924 1.30480919]
[-1.59929924 -0.05784333]
[-1.0068208 -0.34304967]
…
[ 0.77061452 -0.34358523]
[ 0.77061452 -0.27621283]
[ 0.77061452 -0.366081 ]]
筛选过后的数据矩阵的大小： (20940, 2)
决定指标： Index([‘END_DATE’, ‘BASIC_EPS’], dtype=‘object’)
筛选前，模型的精确度： 0.847898758357211
最后一次筛选，模型的精确度：（本次筛选不采纳） 0.8322349570200573
相差： 0.015663801337153616
历史精确度： [0.847898758357211, 0.8554441260744985, 0.8534383954154728, 0.8585482330468004, 0.8681470869149951, 0.8322349570200573]

所以，最终筛选的指标是：[‘END_DATE’, ‘BASIC_EPS’]

筛选过程中，平均精确度如下：

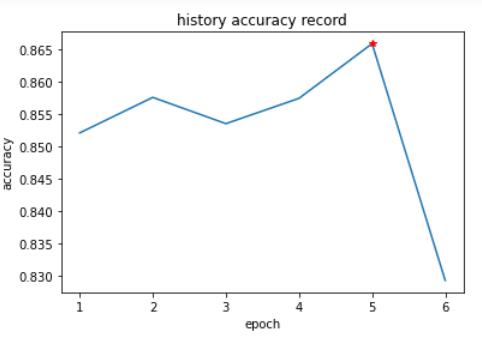
返回目录

第一问最终结果

不是所有行业的数据都像制造业那样，都有 1W+ 的数据。有一些行业的数据，只有个位数。对于这些数据，我们在考虑解决类别不均衡的问题时，要特别注意。比如不能再用欠采样了，过采样时，用于产生新数据的 K 近邻个数肯定不能大于样本量。

过程

解决的过程如“制造业”一样：

返回目录

结果

对于那些数据量比较少的，我们往结果前加一个感叹号。

制造业 行业财务数据造假的决定指标有： END_DATE, OTH_NCA, BASIC_EPS, ASSETS_IMPAIR_LOSS
批发和零售业 行业财务数据造假的决定指标有： C_FR_CAP_CONTR, BASIC_EPS, NOPERATE_EXP
信息传输、软件和信息技术服务业 行业财务数据造假的决定指标有： C_FR_OTH_FINAN_A, N_C_PAID_ACQUIS, BASIC_EPS
！建筑业 行业财务数据造假的决定指标有： GOODWILL, REFUND_OF_TAX, N_C_PAID_ACQUIS, C_FR_MINO_S_SUBS, OTH_GAIN
房地产业 行业财务数据造假的决定指标有： AVAIL_FOR_SALE_FA, BASIC_EPS, NCL_WC, N_TAN_A_TL
！交通运输、仓储和邮政业 行业财务数据造假的决定指标有： N_CF_FA_PROPT, R_TR
！采矿业 行业财务数据造假的决定指标有： Delta_Date, R_D
金融业 行业财务数据造假的决定指标有： LT_AMOR_EXP, AP, C_FR_OTH_INVEST_A, C_FR_OTH_OPERATE_A
农、林、牧、渔业 行业财务数据造假的决定指标有： OTH_RECEIV, MINORITY_INT
教育 行业数据太少, 难以筛选
！电力、热力、燃气及水生产和供应业 行业财务数据造假的决定指标有： INVEST_REAL_ESTATE, OTH_COMPRE_INCOME, ASSETS_DISP_GAIN
文化、体育和娱乐业 行业数据太少, 难以筛选
卫生和社会工作 行业数据太少, 难以筛选
水利、环境和公共设施管理业 行业数据太少, 难以筛选
！科学研究和技术服务业 行业财务数据造假的决定指标有： N_CF_FR_INVEST_A, N_CF_IA_PROPT, N_CF_OPA_PS_YOY, INV_INC_TR
租赁和商务服务业 行业数据太少, 难以筛选
综合 行业数据太少, 难以筛选
住宿和餐饮业 行业数据太少, 难以筛选
居民服务、修理和其他服务业 行业数据太少, 难以筛选

返回目录

第二问

求“第六年”财务造假的企业，也就是要求我们，根据第7年发布的报表，来判断企业是否造假。

注意，这里用的一定要是 发布时间为 7（第7年）的报表。因为报表是一般是年底的呀，而企业是否造假，指的是在出报表之前的那段时间。

其实这一点，数据也告诉我们了。我查了一下，那些 FLAG 为 NAN（带预测），但发布时间为 6 的数据，结果一条都没有。有的只是发布时间为 7 的。

返回目录

时序性？

在筛选数据和特征的时候，特别是筛选特征时，我们需要解决类别不均衡问题。另外，在训练机器学习的时候，当然也需要解决这个问题。

而，在解决类别不均衡问题时，欠采样、过采样早已破坏了数据的时序性。所以，在完后的分析中，便不再考虑数据的时序性了。

返回目录

机器学习方法解决

根据“天下没有免费午餐”定律，在选择一个特定的机器学习算法时，需要从大量的算法中筛选最佳的算法。

我们从下面这些算法中筛选最优算法：

算法	逻辑回归	k近邻算法	朴素贝叶斯分类器	支持向量机分类	决策树	随机森林	AdaBoost
符号	lg	kNN	NB	SVC	dtc	rf	ada

返回目录

筛选最佳参数

不过要从上述算法中，筛选最佳算法，首先要筛选算法的最合适参数。筛选的方法是网格寻优法：

算法	参数网格
lg	无
kNN	{‘n_neighbors’:[3,5,7,9,11,13,15,17,19,21,23,25,27]}
NB	无
SVC	grid = { ‘C’:[0.1,0.25,0.5,0.75,1,1.25,1.5,1.75,2,2.25,2.5,2.75,3,3.25,3.5],‘kernel’:[‘linear’,‘rbf’,‘poly’] }
dtc	grid = {‘max_depth’:[4,9,14,19,24,29,34,39,44,49,54,59,64,69,74,79], ‘ccp_alpha’: [0,0.00025,0.0005,0.001,0.00125,0.0015,0.002,0.005,0.01,0.05,0.1]}
rf	基模型个数：5,15,25,35,45,50,65,75,85,95
ada	基模型个数：5, 15,25,35,45,50,65,75,85,95,105,115,125,135,145,155

最佳结果如下：

返回目录

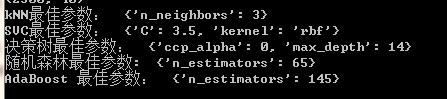
筛选最佳算法

得到最佳参数之后，就可以筛选最佳的算法了。这里我们将所有的最佳参数，用交叉验证，对每一个算法，算出 10 组精确度和均值，结果如下：

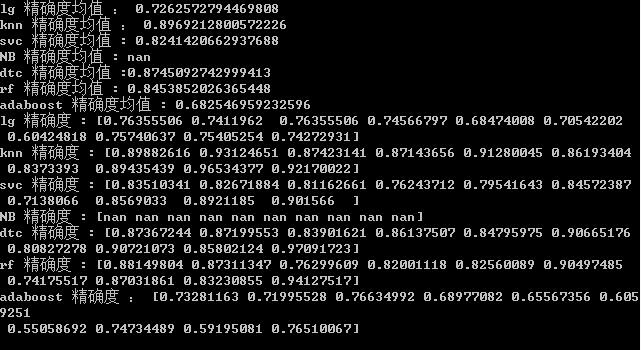
可见：knn 和 dtc 的效果最好。虽然看起来 knn 最好，但记住，我们解决类别不均衡时，用的过采样 ADASYN 产生新数据。所以，用 knn 的效果好，不一定用在其他数据好。所以，这里选择 dtc。

返回目录

效果评价 + 挑出第6年数据造假的企业（股票编号）

将数据按 7:3 拆分成训练集、测试集。用训练集训练 dtc，用测试集评价模型，评价指标还用精确度。之后，用模型求解造假的股票，结果如下所示：

（制造业为例）

返回目录

深度学习方法

这里将构建一个简单的多层感知器，来搭建深度学习模型。

筛选网络拓扑

当然，如何搭建多层感知器呢？神经网络的拓扑结构如何？

根据“没有午餐”定律，我们需要根据模型效果参数。同上，这里再次使用 5 折交叉验证+网格寻优，来筛选最合适的网络拓扑和参数。

参数表格如下：

参数	取值	含义
units_list	[[8,16,8],[5,10,5],[3,8,3]]	隐藏层的层数和对应的神经元个数
‘optimizer’	rmsprop, adam	寻优算法
activation	‘relu’, ‘sigmoid’	激活函数
init	init_uniform, init_normal	节点参数初始化方法
epochs	150, 100, 50	训练迭代次数
batch_size	200, 100, 50	batch 大小
rate	0, 0.1, 0.2	dr 以上是关于2021 泰迪杯 A 题的主要内容，如果未能解决你的问题，请参考以下文章 2021 泰迪杯 C 题 2021 泰迪杯 C 题 2021 泰迪杯 C 题 2021 泰迪杯 A 题思路 2021 泰迪杯 A 题思路 第十一届泰迪杯数据挖掘挑战赛A 题：新冠疫情防控数据的分析 思路+代码（持续更新）