视觉三维重建 | 01 摄像机原理及坐标系转换
Posted AI 菌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了视觉三维重建 | 01 摄像机原理及坐标系转换相关的知识,希望对你有一定的参考价值。
最早接触视觉三维是本科毕设的时候,当时做的是目标检测与三维定位。所以一直想有机会也分享一下视觉三维重建的知识,最近有空,索性就将一些零碎的知识整理分享出来,有问题欢迎大家评论区留言!
一、摄像机针孔模型
如下图所示,是为人熟知的小孔成像模型。相机成像是三维空间中的光线映射到二维图像平面上形成的。
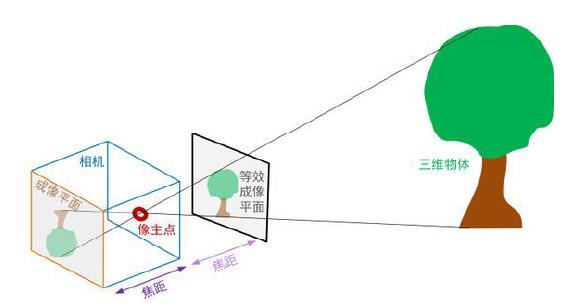
如果将上述模型进行简化,以一个箭头为例,那么它的成像模型如下的:
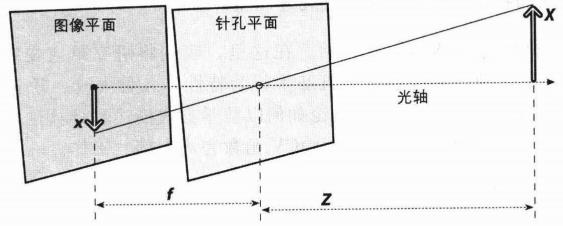
注意:光轴与图像平面的角点被称为主点
由相似三角形,易得: x = f X / Z x=f X/Z x=fX/Z
对于更一般的情况,可得到物体在图像平面上的坐标 (x,y) 和相机坐标系中的坐标
(
X
c
,
Y
c
,
Z
c
)
(X_c, Y_c, Z_c)
(Xc,Yc,Zc) 之间的关系:
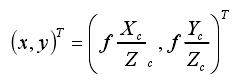
写成矩阵的形式,可表示为:
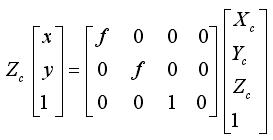
二、像素坐标系到相机坐标系
由于安装过程中的精度,主点往往不在图像平面的正中心位置,所以需要引入偏移量 c x 、 c y c_x、c_y cx、cy 进行建模,即:
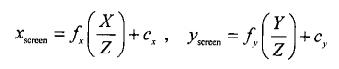
将这个过程更加标准化一下,可写成如下的矩阵形式:
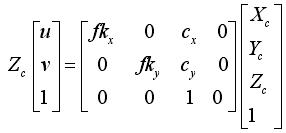
其中,主点在图像的像素坐标为(
c
x
、
c
y
c_x、c_y
cx、cy) ;u、v 分别为 u 轴(x 轴)和 v 轴(y 轴)上的像素坐标;
k
x
k_x
kx 和
k
y
k_y
ky 是将物体单位转换为像素单位的尺度因子,即像素坐标系和像平面坐标系在 u 轴和 v 轴的比例关系。
令
f
x
=
f
k
x
,
f
y
=
f
k
y
f_x=fk_x, f_y=fk_y
fx=fkx,fy=fky,则上式可近一步简化为:
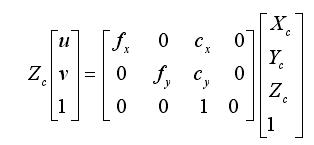
注:上述公式中的
f
f
f 都指代的是相机的实际物理焦距长度,而
f
x
、
f
y
f_x、f_y
fx、fy是相机的像素焦距长度。相机标定获得的是相机的像素焦距长度
f
x
、
f
y
f_x、f_y
fx、fy,而不是实际物理焦距长度
f
f
f。
一般,我们把如下的矩阵 K 称为相机的内参矩阵:

注:K是可以通过相机标定直接获得的,相机标定在后续文章中会具体来讲。
三、像素坐标系到世界坐标系
假设世界坐标系到相机坐标系的旋转矩阵为 R,平移矩阵为 T,则世界坐标系与相机坐标系间的转换关系为:
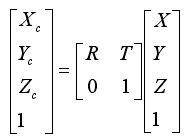
因为,像素坐标系与相机坐标系的关系是:
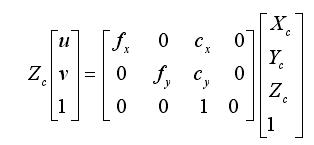
所以,世界坐标系与像素坐标系之间的关系是:
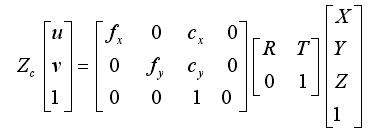
由于水平有限,博客中难免会有一些错误,有纰漏之处恳请各位大佬不吝赐教!

推荐文章
以上是关于视觉三维重建 | 01 摄像机原理及坐标系转换的主要内容,如果未能解决你的问题,请参考以下文章
初探三维计算机视觉(三维重建) —— 相机模型 + 双目系统 + 点云模型