三维视觉 | 04 双目定位/测距原理

Posted 2023-01-18 AI 菌

文章目录

• • 一、双目视觉模型
  • 二、双目标定
  • 三、消除畸变与图像校正
  • • （1） 图像校正
    • （2）图像校正
  • 四. 双目匹配

一、双目视觉模型

由上一节：摄像机原理及坐标系转换 可知，单个相机的像素坐标系与相机坐标系的关系为：

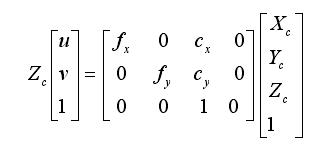
仅仅通过以上的矩阵关系，是无法准确求出目标点的三维位置的，可见单目测距是有局限性的。更一般地，通常会通过双目视觉系统来模拟人的“双眼”，从而判断距离的远近。

在双目视觉的实际应用中，大多数均采用基于平行光轴的视觉模型，如下图所示，$O_l$ 和 $O_r$ 分别是左右相机的光心，空间中的点$P(X_c,Y_c,Z_c)$为待求目标点。

假如我们以左相机的光心为世界坐标系的原点，那么对左相机进行建模可得：

假设右相机相对左相机的旋转矩阵和平移矩阵分别为 R 和 T，那么对右相机进行建模可得：

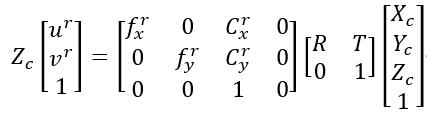
已知相机参数，旋转平移矩阵，左右两图中对应的像素$(u^l,u^l)$和 $(u^r,u^r)$，通过以上两个式子，其实就可以求解空间中的点$P(X_c,Y_c,Z_c)$。

那么，下面就具体来谈谈双目定位/测距的过程！

二、双目标定

通过双目标定可以获取左右相机自己的内部参数 R 和外部参数 T，具体获取方法可见：

• 三维视觉 | 03 MATLAB 单、双目相机标定

三、消除畸变与图像校正

（1） 图像校正

• 径向畸变：由于镜头形状造成的，比如正方形物体经过圆形的镜头，在图像平面上呈现是弯曲的。并且随着向边缘的移动，畸变越来越严重。
  消除方法：由于实际过程中畸变较小，可以用r=0位置进行泰勒级数展开：
  
• 切向畸变：当镜头不完全平行于图像平面的时候产生的。主要是在镜头制造过程中产生的。
  消除方法：用两个参数P1和P2来描述
  

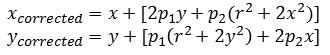
（2）图像校正

调整摄像机之间的角度和距离，输出行对准的校正图像。

四. 双目匹配

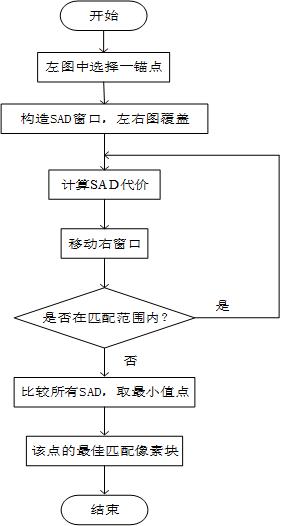
SAD(Sum of absolute differences)是一种简单的图像匹配算法，其基本流程为：

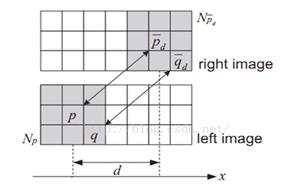
• 构造一个小窗口，类似与卷积核。
• 用窗口覆盖左边的图像，选择出窗口覆盖区域内的所有像素点。
• 同样用窗口覆盖右边的图像并选择出覆盖区域的像素点。
• 左边覆盖区域减去右边覆盖区域，并求出所有像素点差的绝对值的和。
• 移动右边图像的窗口，重复3，4的动作。（这里有个搜索范围，超过这个范围跳出）
• 找到这个范围内SAD值最小的窗口，即找到了左边图像的最佳匹配的像素块。