路径规划蚁群算法求解多中心vrp问题matlab

Posted 2021-06-24 MatlabQQ1575304183

​​​​​​

一、蚁群算法简介

　　蚁群算法(AG)是一种模拟蚂蚁觅食行为的模拟优化算法，它是由意大利学者Dorigo M等人于1991年首先提出，并首先使用在解决TSP（旅行商问题）上。

      之后，又系统研究了蚁群算法的基本原理和数学模型.

二、蚁群算法原理

1、蚂蚁在路径上释放信息素。

2、碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。

4、最优路径上的信息素浓度越来越大。

5、最终蚁群找到最优寻食路径。

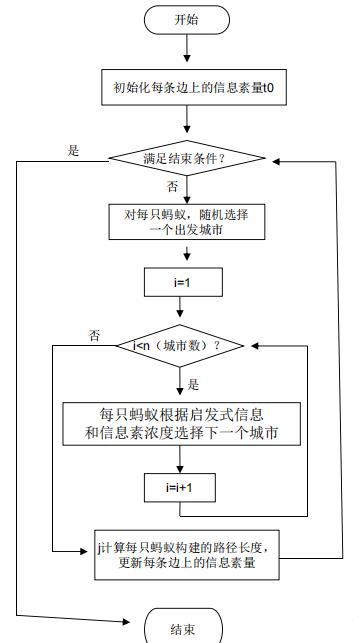
三、蚁群算法流程图

clc;
clear;
%% 多配送中心的车辆调度问题
%加载数据
load data.mat
%计算位置矩阵
m=size(X,1);
D=zeros(m,m);
for i=1:m
    for j=1:m
        D(i,j)=norm(X(i,:)-X(j,:));
        D(j,i)=D(i,j);
        D(i,i)=eps;
    end
end
%计算配送中心的位置
nume=zeros(20,20);
for i=1:20
    for j=1:20 
        temp=[D(:,i) D(:,j)];
        [num,pp]=min(temp,[],2);
        nume(i,j)=sum(num);
    end
end
[mum1,index1]=min(nume);
[mun2,index2]=min(mum1,[],2);
w1=index1(index2);
w2=index2;
%给各个配送中心分配顾客集
H=[];
S=[];
for i=1:20
    if D(i,w1)<D(i,w2)
        H=[H i];
    else 
        S=[S i];
    end
end
n1=size(H,2);
n2=size(S,2);
%蚁群算法求最小的车辆总行程
%设置参数
Pop=60;%蚁群数目
Alpha=1;%重要度系数
Beta=1;%Beta：能见度系数
gama=2;
Rho=0.15;%挥发度系数
MAXGEN=50;%迭代次数
Q=15;%信息更新参数
W=9;%W:车辆载重量
T=10;
w=[2.5,1.5,1.8,2.0,0.8,1.5,1.0,2.5,3.0,1.7,0.6,0.2,2.4,1.9,2.0,0.7,0.5,2.2,3.1,0.1];%每个客户所需的货物重量
t=[1.5,3.8,0.5,3,2.6,3.6,1.4,2.4,2,3.4,2,1.2,0.5,0.8,1.3,1.6,1.7,0.5,0.8,1.4];%每个客户所需的货物的容积
load_w_H=0;
load_t_H=0;
load_w_S=0;
load_t_S=0;
Eta=1./D;%启发因子，设为距离的倒数
Tau_H=ones(m,m);%信息素矩阵
Tau_S=ones(m,m);
Tabu_H=zeros(Pop,n1+10);%存储并记录路径的生成
iter=1;
G_best_route_H=[MAXGEN,n1+10];%各代最佳路线 
G_best_route_S=[MAXGEN,n2+10];
G_best_length_H=zeros(MAXGEN,1);
G_best_length_S=zeros(MAXGEN,1);
length_ave_H=zeros(MAXGEN,1);%各代路线的平均长度
length_ave_S=zeros(MAXGEN,1);
G_best_length=zeros(MAXGEN,1);
%开始进行迭代
while iter<=MAXGEN
    Tabu_H(:,1)=w1*ones(Pop,1);
    Tabu_S(:,1)=w2*ones(Pop,1);
 for i=1:Pop
        visited_H=Tabu_H(i,:);
        visited_H=visited_H(visited_H>0);
        to_visit_H=setdiff(H,visited_H);
        visited_S=Tabu_S(i,:);
        visited_S=visited_S(visited_S>0);
        to_visit_S=setdiff(S,visited_S);
        j=1;d=1;
 while j<=n1
 if ~isempty(to_visit_H)
%按照规则选下一个工厂或者是回到仓库
  x=to_visit_H;
 for k=1:length(to_visit_H)
  x(k)=(Tau_H(visited_H(end),to_visit_H(k))^Alpha)*(Eta(visited_H(end),to_visit_H(k))^Beta);
 end
 x=x/(sum(x)); 
%按概率原则选取下一个城市 
XC=cumsum(x); 
Select=find(XC>=rand);
if isempty(Select)
    Select=w1;
    load_w_H=load_w_H+w(Select);
    load_t_H=load_w_H+t(Select);
else
load_w_H=load_w_H+w(to_visit_H(Select(1)));
load_t_H=load_t_H+t(to_visit_H(Select(1)));
end
c1=min((load_w_H)-9,0);c2=min((load_t_H)-10,0);
if c1<0&&c2<0
    Tabu_H(i,length(visited_H)+1)=to_visit_H(Select(1)); 
else
    Select=w1;
       j=j-1;
    load_w_H=0;
    load_t_H=0;
    Tabu_H(i,length(visited_H)+1)=Select;
end
end
    visited_H=Tabu_H(i,:);
    visited_H=visited_H(visited_H>0);
    to_visit_H=setdiff(H,visited_H);
     if visited_H(end)~=w1
   Tabu_H(i,1:(length(visited_H)+1))=[visited_H,w1];
     end
           j=j+1;
 end
  %第二个配送中心
  while d<=n2
 if ~isempty(to_visit_S)
%按照规则选下一个工厂或者是回到仓库
  x=to_visit_S;
 for k=1:length(to_visit_S)
  x(k)=(Tau_S(visited_S(end),to_visit_S(k))^Alpha)*(Eta(visited_S(end),to_visit_S(k))^Beta);
 end
 x=x/(sum(x)); 
%按概率原则选取下一个城市 
XC=cumsum(x); 
Select=find(XC>=rand);
if isempty(Select)
    Select=w2;
    load_w_S=load_w_S+w(Select);
    load_t_S=load_w_S+t(Select);
else
load_w_S=load_w_S+w(to_visit_S(Select(1)));
load_t_S=load_t_S+t(to_visit_S(Select(1)));
end
c1=min((load_w_S)-9,0);c2=min((load_t_S)-10,0);
if c1<0&&c2<0
    Tabu_S(i,length(visited_S)+1)=to_visit_S(Select(1)); 
else
    Select=w2;
       j=j-1;
    load_w_S=0;
    load_t_S=0;
    Tabu_S(i,length(visited_S)+1)=Select;
end
end
    visited_S=Tabu_S(i,:);
    visited_S=visited_S(visited_S>0);
    to_visit_S=setdiff(S,visited_S);
     if visited_S(end)~=w2
   Tabu_S(i,1:(length(visited_S)+1))=[visited_S,w2];
     end
           d=d+1;
  end
    load_w_H=0;
    load_t_H=0;
    load_w_S=0;
    load_t_S=0;
    x=[];
 end
%% 第四步记录本代各种参数，计算各只蚂蚁的路程
L_H=zeros(Pop,1); 
L_S=zeros(Pop,1);
for i=1:Pop 
MM_H=Tabu_H(i,:); 
MM_S=Tabu_S(i,:);
R_H=MM_H(MM_H>0);
R_S=MM_S(MM_S>0);
for j=1:(length(R_H)-1)
L_H(i)=L_H(i)+D(R_H(j),R_H(j+1)); 
end 
for k=1:(length(R_S)-1)
L_S(i)=L_S(i)+D(R_S(k),R_S(k+1)); 
end 
end
%计算最短距离和最短路径 
[min_Length_H,index_H]=min(L_H);
[min_Length_S,index_S]=min(L_S);
G_best_length_H(iter)=min_Length_H;
G_best_length_S(iter)=min_Length_S;
G_best_route_H(iter,1:length(Tabu_H(index_H(1),:)))=Tabu_H(index_H(1),:);
G_best_route_S(iter,1:length(Tabu_S(index_S(1),:)))=Tabu_S(index_S(1),:);
%% 应用2-opt方法对最优解进行更新
%对第一个配送中心的最优解进行优化
select=find(G_best_route_H(iter,:)==w1);
FF_H=[];
LM_H=0;
for a=1:(length(select)-1)
   y_G_best_route_H=G_best_route_H(iter,select(a):select(a+1));%%每一个解中每一个车辆路径
   al=length(y_G_best_route_H);
   T=zeros((length(select)-1),1);
   for d=1:(al-1)
       T(a)=T(a)+D(y_G_best_route_H(d),y_G_best_route_H(d+1));%%每一个解中每一个车辆路程
   end
   %交换车辆顺序
   for b=2:(al-1)
       for c=(b+1):(al-1)
           DD=y_G_best_route_H;
           temp1=DD(b);
           temp2=DD(c);
           DD(b)=temp2;
           DD(c)=temp1;
           TT=zeros(1);
           for d=1:(al-1)
       TT=TT+D(DD(d),DD(d+1));% 得到的新解的路程
           end
           if TT<T(a)
               T(a)=TT;
            y_G_best_route_H=DD;
           end
       end
    end
   if a>=2
       y_G_best_route_H=y_G_best_route_H(2:al);
   end
   FF_H=[FF_H y_G_best_route_H];
   LM_H=LM_H+T(a);
end
   G_best_length_H(iter)=LM_H;
   G_best_route_H(iter,1:length(FF_H))=FF_H;
   G_best_length(iter)=G_best_length_H(iter)+G_best_length_S(iter);
   FF_H=[];
   LM_H=0;
 %第一个配送中心的2-opt优化完毕
length_ave(iter)=mean(L_H+L_S);
disp(['第',num2str(iter),'代']);
iter=iter+1;
%% 第五步更新信息素
Delta_Tau_H=zeros(m,m); 
Delta_Tau_S=zeros(m,m);
for i=1:Pop 
MM_H=Tabu_H(i,:); 
MM_S=Tabu_S(i,:);
R_H=MM_H(MM_H>0);
R_S=MM_S(MM_S>0);
for j=1:(length(R_H)-1) 
Delta_Tau_H(R_H(j),R_H(j+1))=Delta_Tau_H(R_H(j),R_H(j+1))+Q/L_H(i); 
end 
for k=1:(length(R_S)-1) 
Delta_Tau_S(R_S(k),R_S(k+1))=Delta_Tau_S(R_S(k),R_S(k+1))+Q/L_S(i); 
end 
end 
Tau_H=(1-Rho).*Tau_H+Delta_Tau_H;
Tau_S=(1-Rho).*Tau_S+Delta_Tau_S;
%% 第六步：禁忌表清零 
Tabu_H=zeros(Pop,n1); 
load_w_H=0;
Tabu_S=zeros(Pop,n2); 
load_w_S=0;
end
%% 第七步：输出结果 
[best_length_H,index_H]=min(G_best_length_H);
[best_length_S,index_S]=min(G_best_length_S);
best_length=best_length_H+best_length_S;
best_route_H=G_best_route_H(index_H(1),:);
best_route_H=best_route_H(best_route_H>0);
best_route_S=G_best_route_S(index_S(1),:);
best_route_S=best_route_S(best_route_S>0);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~');
disp(['最短路径为：',num2str(best_route_H)]);
disp(['           ',num2str(best_route_S)]);
disp(['最短路程为：',num2str(best_length)]);
%% 第八步：绘制散点图和巡游过程图
%画出散点图，并标注配送中心的位置
figure(1)
plot(X(:,1),X(:,2),'o');
hold on
plot(X(best_route_H,1),X(best_route_H,2),'o-');
plot(X(best_route_S,1),X(best_route_S,2),'o-');
%plot([X(w1,1),X(w2,1)],[X(w1,2),X(w2,2)],'rs','MarkerSize',9);
text([X(w1,1),X(w2,1)],[X(w1,2),X(w2,2)],'\\leftarrow 配送中心');
for i=1:m
    text(X(i,1),X(i,2),['  ' num2str(i)]); 
end
figure(2)
plot(1:MAXGEN,G_best_length) ;
hold on 
plot(1:MAXGEN,length_ave);
xlabel('迭代次数/次');
ylabel('路径长度/km');
legend('最优路径长度的变化 ',' 路径长度均值变化 ');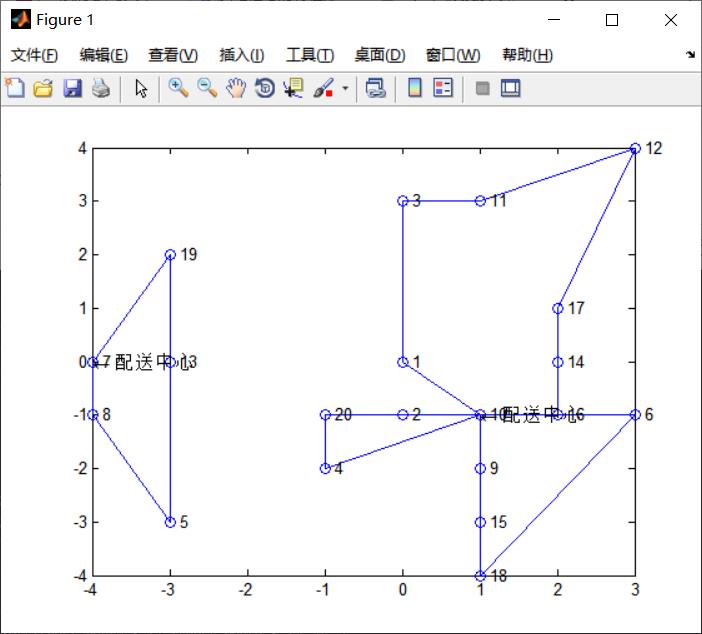

​

完整代码或者仿真咨询添加QQ1575304183