《数字图像处理》学习总结及感悟:第二章数字图像基础数学工具
Posted LaoYuanPython
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《数字图像处理》学习总结及感悟:第二章数字图像基础数学工具相关的知识,希望对你有一定的参考价值。


☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░
一、引言
本系列文章记录老猿自学冈萨雷斯《数字图像处理》的感悟和总结,不过估计更新会比较慢,白天要工作,都是晚上抽空学习,学习完一章再回头总结,想学的朋友可以自己下载英文原版(目前到第四版)和中文译本(目前应该到第三版)的电子版观看,如果想对照观看建议英文原版也找第三版。
这本《数字图像处理》不愧为数字图像处理的经典教程,知识范围广、内容详尽、案例贴近实践,至少很合老猿的口味。但中译本存在两个问题:
- 有些翻译得不够精准或流利,对于这样的内容如果在老猿总结知识中出现,会以斜体字标记,有些关键术语老猿会附上英文原词;
- 中译本的图像案例很多都比原版差很多,甚至差到影响对讲述内容的理解,因此就算不看原版文字,图像案例最好还是对照原版的。
二、知识概要: 数字图像处理所用数学工具( the Mathematical Tools Used in Digital Image Processing)
本部分简单介绍图形处理需要用到的数学知识和工具。
2.1、阵列和矩阵操作(Array versus Matrix Operations)
数字图像以行和列的方式存储像素的值,这种存储方式成为阵列(array),看起来与矩阵(matrix)存储数据是一样的,实际上图像的很多操作是基于矩阵方式执行的,但有时候基于阵列的图像操作和矩阵操作相差很大。
除非特别说明,在相关处理中都假设是阵列操作而不是矩阵操作。对于阵列的操作是将阵列的操作直接作用到阵列的每个像素元素上,如两个阵列相加就是两个阵列相同位置的元素直接相加,减法、乘法、除法一样,求幂运算就是对阵列中的每个元素求幂,所有图像的算术操作全部都是阵列操作。
以4个元素的阵列和矩阵乘法举例,阵列乘法运算和矩阵乘法的区别如下:
-
阵列乘法
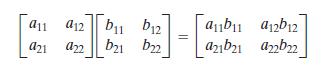
-
矩阵乘法
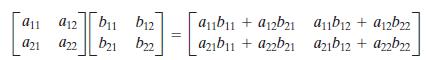
2.2、线性和非线性操作(Linear versus Nonlinear Operations)
假设作用在图像f(x,y)上的算子H使得:
H[f(x, y)] = g(x, y)
且满足:
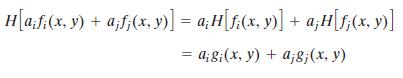
其中ai、aj是任意常数,fi和fj是任意两个大小相同的图像,则称H为线性操作。
非线性操作则比线性操作难以理解,使用不多,但有时性能会远优于线性操作,某些特定处理需要用到。
2.3、图像算术运算(Arithmetic Operations)
图像的算术操作全部都是阵列操作,具体操作内容很简单,在此老猿不多说。
在这里介绍一下它们的应用举例:
- 图像加法操作可用于图像降噪(noise reduction),这一般用于图像在各点的噪声是不相关的,是加性噪声,如天文学观察由于非常低的照度下成像会导致传感器噪声,导致单幅图像无法分析,通过多幅图像相加再平均即可以降噪
- 图像减法操作可以用于增强图像之间的差别,如血管造影照和造影前的血管照相减可以获得造影剂在血管内的分布情况
- 图像相乘可以用一个模板图像与对应图像相乘从而留下感兴趣的ROI区域,即ROI区域对应的模板区域元素设置为1,其他区域设置为0,再进行图像和模板相乘即可获得ROI区域。
- 图像相乘或相除可以用于阴影校正(shading correction),老猿理解阴影是由于光学折射不均匀导致的镜头周围出现阴影,例如一张白纸的照片打印出来时并不是白色或颜色一致的背景,而是有分布不均匀的背景色,下图左边是一个钨丝放置在颜色单一背景的情况照片、中间是单一背景的照片,照片中明显有阴影,右边是进行阴影校正后的图片:

采用左边图像除以中间图像再进行处理后就可以得到右边图像。
假设除法运算的结果图像为f(x,y),要保证运算结果最后落入某个固定比特数表示的范围的运算过程如下:
fmin = f - min(f)
fmin = fmin + v #加v是为了避免除数为0,v为一大于0的非常小的数,按具体数据类型来确认,如果为整型则v=1
fresult = K*(fmin/max(fmin)),k为一图像灰度所能达到的最大值,如图像灰度是8bit,则k=255
老猿认为上述处理就是归一化处理,不过该归一化处理算法与OpenCV的归一化处理不同,OpenCV归一化处理请见《OpenCV-Python图像乘法运算cv2.multiply函数详解及像素值溢出归一化处理》。
2.4、图像的集合运算和逻辑运算(Set Operations)
图像的灰度集合操作是针对一幅或多幅图像的整体进行的操作,包括图像像素位置和图像灰度的操作。
像素位置的集合操作
集合运算包括集合的子交并补运算,当集合运算是对图像的像素操作时,对应运算就是简单的子交并补。需要注意的是,一般将图像的全集(universe)定义为包含图像中所有像素的矩形,全集一般记为U。
当两个集合A和B相减时,其结果等于A和Bc(即B的补集)的交集。
灰度值的集合操作
- 两个图像灰度的并集取A/B每个相同位置对应像素的最大灰度作为结果图像同样位置的像素灰度
- 两个图像灰度的交集取A/B每个相同位置对应像素的最小灰度作为结果图像同样位置的像素灰度
- 补集操作为某个常数K减去每个像素的灰度值所得的图像(常数K为《数字图像处理》学习感悟:第二章(3)采样、量化和插值》所定义的图像灰度分辨率n的2n-1,n是表示该图像灰度值的比特数)。
另外图像中还会用到模糊集合(Fuzzy sets)的概念,这个暂时不展开多说。
2.5、图像的逻辑运算( Logical Operations)
逻辑运算包括与或非和异或,与或非三个运算是功能完备的,任何其他逻辑操作都可以通过这三个运算获得。两幅图像的逻辑操作就是这两幅图像的像素对之间的逻辑运算操作。
图像的或操作。而Not操作则是对灰度值的求补操作。
2.6、空间操作(Spatial Operations)
2.6.1、定义
空间操作是指操作直接作用于给定图像像素上的操作,包括单像素操作(single-pixel operations)、邻域操作(neighborhood operations)和几何空间变换(geometric spatial transformations)。
- 单像素操作:操作运算直接对图像每个像素的灰度值进行,不和其他像素发送关系
- 邻域操作:对图像的任意一点,其目标图像的灰度值由原图像中该点周围的邻域像素经指定操作处理决定
- 几何空间变换:几何变换是变换图像中像素间的空间关系(spatial relationship)。几何变换又称为橡皮膜变换(rubber-sheet transformations),可以看成将一副图像印刷在橡皮膜上,然后根据一定的规则拉伸该薄膜形成图像变换。
几何变换由坐标的空间变换(spatial transformation of coordinates)和对于空间变换后的像素的灰度使用灰度插值(intensity interpolation)进行计算组成。
2.6.2、空间操作案例–仿射变换
最常用的空间变换是仿射变换(affine transform),仿射变换公式表示如下:
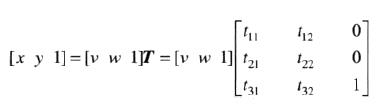
对于上述仿射变换公式,T称为仿射变换矩阵。
上述公式可以通过输入图像各像素的灰度值来计算输出图像中映射位置的灰度值,但这种方式可能存在多个输入图像像素映射到一个输出图像像素、或者某个输出图像像素没有计算出的值填入等问题,这种通过输入图像像素计算输出图像映射到的像素灰度值的方法称为前向映射(forward mapping)。
还有种方式,就是根据输出图像的像素位置,使用变换矩阵的逆矩阵计算该位置在输入图像中的像素位置,然后根据该输入图像像素的位置使用插值法来确认输出像素的灰度值,这种方式称为反向映射(inverse mapping)。反向映射比前向映射更有效,被许多商业软件所使用。
关于仿射变换更多的内容请参考《https://blog.csdn.net/LaoYuanPython/article/details/113832562 OpenCV-Python图像处理:仿射变换详解及案例》的介绍。
2.6.3、空间操作案例–图像配准(Image Registration)
2.6.3.1 定义
图像配准是用于对齐两幅或多幅相同景物(scene)的图像,在图像配准时,有可用的输入图像和输出图像,但怎么从输入图像变换到输出图像即变换函数是未知的,这里的输入图像就是要变换的图像,而输出图像就是参考图像,它用于配准输入图像的图像。
注:老猿认为这里说的输出图像仅是理论上的,如果真正在进行配准时,只能说是参考图像,否则已有输出图像,为什么还要配准呢?
之所以要配准图像,是因为在景物成像过程中,由于观察视角(viewing angle)、距离、方向、传感器分辨率、目标位置移动(shift)及其他因素导致图像几何畸变,对这些畸变进行修正就需要图像配准,通过配准后合并这些图像或执行图像的定量分析。
2.6.3.2、配准方法
进行图像配准的主要方法之一是使用约束点(tie points,也称为控制点,control points),这些点是输入图像和参考图像中期位置已知的相应点。约束点可以交互式选择或自动选择。有了足够约束点后,就可以推导出变换函数。
4个约束点的近似双线性变换公式如下:

其中v、w是原图像中像素的坐标,x、y是变换后的坐标。
如果四个点不能校准一个图像,可以将图像划分成多个不重叠的子图像,每个子图像用4个点来校准,这样叠加进行整个图像校准。
但是当畸变很严重时,使用约束点很难实现完美的匹配,另外手工选择约束点的误差一般比较大。

上面4个图像,按从左到右再从上到下编号为a、b、c、d,a是参考图像,b是产生了几何畸变的输入图像,c是配准后的输出图像,d是配准后的输出图像和参考图像的差异。
2.6.3.3 、老猿理解:
- 图像配准就是借助于出现不同畸变的图像中的相同景物相同位置的参考点,通过这些点在不同图像中的空间位置就可以获得对应的变换函数,然后将这个变换函数作用于整个输入图像,就可以获得输入图像与配准图像相同成像环境(包括视角、方向、距离、分辨率和位置等)的近似图像
- 这个过程有点类似求解n元k次方程的各个系数,求解前需要找到足够的未知数的值对代入,这样才能计算出相关系数。约束点的数量和变换函数模型的复杂度取决于要配准图像的畸变程度,例如如果只是景物平移导致的畸变,也许只需要有1个控制点的2元一次方程就可以了,如果是角度旋转的畸变,就需要4个约束点。
- 配准对应的变换实际上就是类似透视变换的变换,只是变换矩阵未知,需要通过约束点求变换矩阵(超过4个约束点求得的矩阵已经不是3×3的矩阵)
2.7、向量与矩阵操作(Vector and Matrix Operations)
多光谱图像处理(Multispectral image processing)是使用向量和矩阵操作的典型领域。一个RGB彩色图像的像素包含3个分量,这三个分量可以组成一个三维的列向量。
像素被表示为向量后,就可以使用向量和矩阵相关的处理理论和工具。有关向量的知识介绍请参考《https://blog.csdn.net/LaoYuanPython/article/details/112410587 人工智能数学基础-线性代数1:向量及向量加减法与数乘》和《https://blog.csdn.net/LaoYuanPython/article/details/112411742 人工智能数学基础-线性代数2:向量的点积、內积、数量积和外积》的介绍。
整个图像都可以被当作矩阵或向量来处理,例如图像的线性处理:
g = Hf + n
其中,f表示输入图像,是一个MN×1的向量。n表示M×N的噪声模式的MN×1向量,g表示输出图像,也是一个MN×1的向量。
2.8、图像变换(Image Transforms)
数字图像f(x,y)的坐标张成的实平面(real plane)称为空间域(spatial domain),x、y称为空间变量(spatial variables )或空间坐标(spatial coordinates),基于像素坐标到像素坐标的变换是基于空间域进行的变换。
而有些情况下,图像处理任务这样来构建最好(best formulated):变换输入图像、在变换域(transforms domain)执行特定任务,执行完后再将处理完成后的结果反变换(inverse transform)回到空间域。
如表示为T(u,v)的二维线性变换,其通用形式表示为:
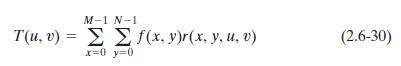
其中f(x,y)是M行N列的输入图像,r(x,y,u,v)称为正变换核(forward transformation kernel,也称为前向变换核),,对上述公式使用u=0,1,…,M-1,v=0,1,…,N-1进行计算,u、v称为变换变量(transform variables),T(u,v)称为f(x,y)的正变换(forward transform,也称为前向变换)。
给定T(u,v)后,可以用其逆变换(inverse transform,也叫反变换)还原f(x,y):
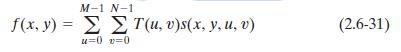
s(x,y,u,v)称为逆变换核(inverse transformation kernel,也可翻译为“反变换核”)。
上面的两个变换公式(2.6-30)和(2.6-31)一起称为变换对(transform pair)。下图是上面介绍的二维线性变换执行图像处理的基本步骤:
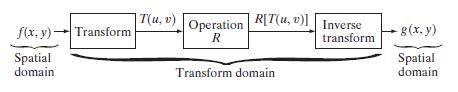
对应的变换域为线性变换域(linear transform domain)。
如果公式(2.6-30)中的正变换核:r(x,y,u,v)=r1(x,u)r2(y,v),那么则称正变换核是可分的(separable)。如果在此基础上,r1(x,y)等于r2(x,y),则称变换核是对称的(symmetric)。此时r(x,y,u,v)=r1(x,u)r1(y,v)。如果上述描述中的正变换核r换成逆变换核s,同样适用于逆变换核。
傅里叶变换在图像处理中是一种很常用的变换方法,可以使图像从空间域转换到频率域从而进行一些图像处理操作。傅里叶变换就是可分的和对称的,并且可分的和对称的核允许用一维傅里叶变换计算二维傅里叶变换。
二维傅里叶变换(Fourier transform)的正变换核:
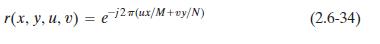
逆变换核为:
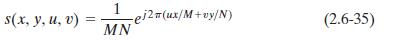
将其带入式(2.6-30)和(2.6-31),可以得到离散傅里叶变换对(discrete Fourier transform pair):
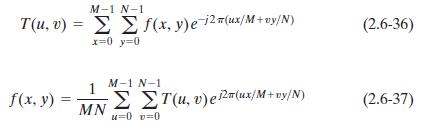
当变换对的正反核是可分的和对称的,且图像f(x,y)是大小为M×M的方形图像时,上面的公式(2.6-30)和(2.6-31)可表示为矩阵形式:

其中,F是代表包含元素f(x, y)的图像的M阶方形矩阵,A是带元素aij=r1(i,j)的M阶方阵,T是M×M的变换结果,其值为T(u,v),u,v取值为[0,M-1]。
为了得到逆变换,我们用逆变换矩阵(inverse transformation matrix)B前乘和后乘(pre- and post-multiply)式(2.6-38):

如果B=A-1,即B是A的逆矩阵,则:

上面的公式表明,图像F可以由其正变换完全还原。
变换域
老猿理解空间变换就是能用矩阵运算表达的变换(没有求证过,如果有大佬愿意指教非常欢迎)。而有些情况下,将输入图像进行非矩阵运算的处理(如傅里叶变换),就需要先将图像变换成对应域。关于变换域老猿花了将近一整天的时间去理解,最后单独发了篇博文《https://blog.csdn.net/LaoYuanPython/article/details/117389597 图像处理空间域、变换域、时域和频域的含义理解:spatial VS transforms domain》,在此就不多说了。
2.9、 概率方法(Probabilistic Methods)
概率论中的概率计算、均值、方差(请参考《https://blog.csdn.net/LaoYuanPython/article/details/108864527 人工智能数学基础4:离差、平均差、方差、标准差、协方差、皮尔森相关系数》的介绍)、随机变量(random variable)、n阶矩(nth-moment)等在图像处理特别是灰度处理应用中都有重要应用,在此就不单独展开介绍。
三、小结和感悟
本节概要性地介绍了图像处理所使用的数学工具,包括阵列与矩阵操作、线性操作和非线性操作、算术操作、集合和逻辑操作、空间操作、向量与矩阵操作、图像变换和概率方法。这些数学方法在接下来的图像处理过程中会或多或少的使用到,熟悉这些数学方法和工具对于理解图像处理的方法非常重要。
更多图像处理请参考专栏《OpenCV-Python图形图像处理》及《图像处理基础知识》的介绍。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《 专栏:Python基础教程目录》从零开始学习Python。
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
关于老猿的付费专栏
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程,对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏,是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合,相关资料基本上都是老猿反复研究的成果,有助于OpenCV-Python初学者比较深入地理解OpenCV,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容,包括爬虫入门的基础知识,以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。
前两个专栏都适合有一定Python基础但无相关知识的小白读者学习,第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏:Python基础教程目录)从零开始学习Python。
如果有兴趣也愿意支持老猿的读者,欢迎购买付费专栏。
老猿Python,跟老猿学Python!
☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░
以上是关于《数字图像处理》学习总结及感悟:第二章数字图像基础数学工具的主要内容,如果未能解决你的问题,请参考以下文章
《数字图像处理》学习总结及感悟:第二章数字图像基础像素间的关系
《数字图像处理》学习总结及感悟:第二章数字图像基础电磁波传感器及辐射成像原理