数据结构，加权图的最短路径，导游程序

Posted 2021-06-22 小偷12138

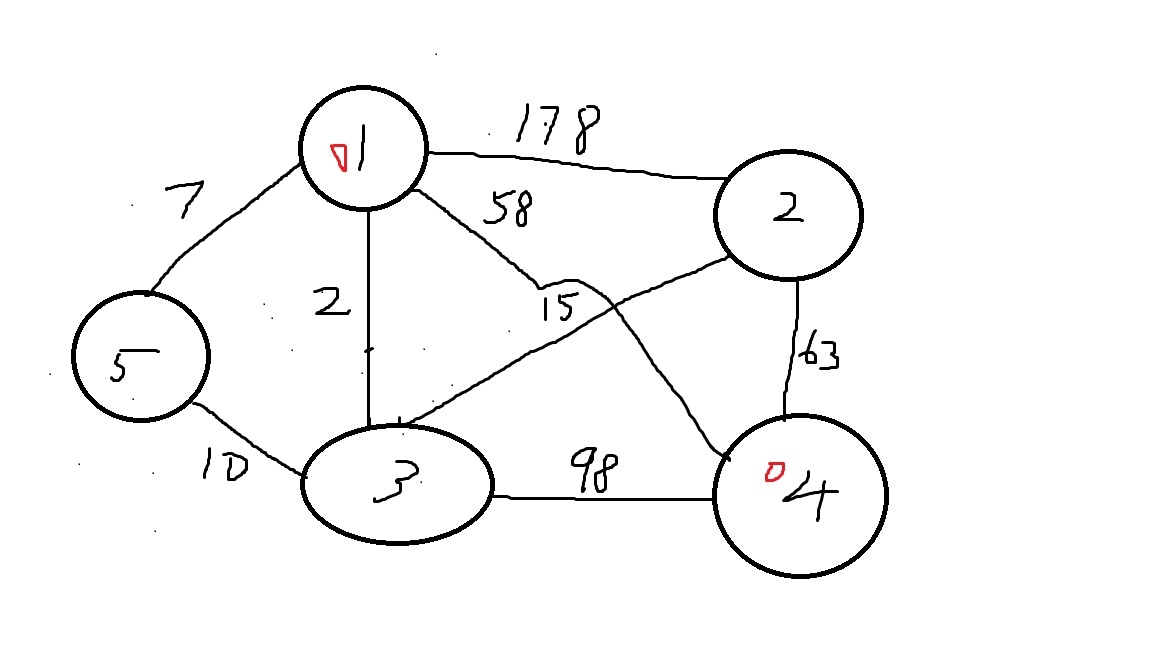
txt文件格式

#include <iostream>
#include <fstream>
using namespace std;
typedef struct information
{
    int number;//编号
    char name[50];//名称
    char lntroduction[50];//简介
    information** path[10];//路径
    int distance[10];//距离
    int key;
}inform;
class Figure
{
private:
    char a[50];
    char s[5];
    int i, k, j , m;
    int h, g[10];
public:
    int min, max, g1[10];//路径，距离
    inform* p[10];
	Figure(const char *ss);//从文件读取数据
	~Figure();
    int _path(inform* p1, inform* p2);//最短路径
    void enquiry_path(inform* p1, inform* p2);
    void enquiry(int i);
};
Figure::Figure(const char *ss){
    i = 0, k = 0, j = 14, m = 0;
    memset(p, 0, 10 * 4);
    memset(a, 0, 50);
    memset(s, 0, 5);
    ifstream inFile(ss, ios::in);
    while (!inFile.eof()) {
        k = 0, j = 0, m = 0;
        p[i] = new inform();
        memset(a, 0, 50);
        inFile.getline(a, 100);
        for (unsigned int ii = 6; ii <= strlen(a); ii++)
            s[ii - 6] = a[ii];
        p[i]->number = atoi(s);
        memset(s, 0, 5);
        memset(a, 0, 50);
        inFile.getline(a, 100);
        memcpy(p[i]->name, a, 50);
        memset(a, 0, 50);
        inFile.getline(a, 100);
        memcpy(p[i]->lntroduction, a, 50);
        memset(a, 0, 50);
        inFile.getline(a, 100);
        for (unsigned int ii = 12; ii <= strlen(a); ii++)
        {
            if (a[ii] > 0) {
                s[k] = a[ii];
                k++;
            }
            else {
                k = 0;
                p[i]->path[j++] = &p[atoi(s) - 1];
                memset(s, 0, 5);
                ii++;
            }
        }
        j = 0;
        memset(a, 0, 50);
        inFile.getline(a, 100);
        for (unsigned int ii = 14; ii <= strlen(a); ii++)
        {
            if (a[ii] > 0) {
                s[k] = a[ii];
                k++;
            }
            else {
                k = 0;
                p[i]->distance[j++] = atoi(s);
                memset(s, 0, 5);
                ii++;
            }
        }
        memset(a, 0, 50);
        inFile.getline(a, 100);
        i++;
    }
}
Figure::~Figure()
{
    for (int ii = 0; ii < i; ii++)
    {
        delete p[ii];
    }
}
void Figure::enquiry(int i) {
    cout << "编号：" << p[i]->number << endl;
    cout << p[i]->name << endl;
    cout << p[i]->lntroduction << endl;
}
void Figure::enquiry_path(inform* p1, inform* p2) {
    min = 0, max = 999, h = 0;
    memset(g, 0, 10 * sizeof(int));
    memset(g1, 0, 10 * sizeof(int));
    _path(p1,p2);
    cout << "最短距离：" << max << endl;
    cout << "路径编号：" << p1->number;
    for (int i = 0; g1[i] != 0; i++)
        cout << "---" << g1[i];
    cout << endl;
}
int Figure::_path(inform* p1, inform* p2)
{
    if (p1->key == 1)return 0;//判断是否访问过
    p1->key = 1;
    for (int i = 0; p1->path[i] != 0; i++)
    {
        if ((*(p1->path[i]))->key == 1)continue;
        min = min + p1->distance[i];       //
        g[h++] = (*(p1->path[i]))->number;//添加路径
        if ((*(p1->path[i])) == p2){
            if (min < max) {
                max = min;
                memcpy(g1, g, 10 * sizeof(int));
            };
            min = min - p1->distance[i];//
            g[--h] = 0;                //返回路径
            continue;
        }
        _path((*(p1->path[i])), p2);
        min = min - p1->distance[i];//
        g[h--] = 0;                //返回路径
    }
    p1->key = 0;
    return 0;
}
int main()
{
    int a = 0, i = 0, j = 0;
    Figure aa("a.txt");
    cout << "输入1查询路径" << endl;
    cout << "输入2查询信息" << endl;
    cout << "输入3退出" << endl;
    cout << "-------------" << endl;
    while (true)
    {
        cout << "输入选项" << endl;
        cout << "-------------" << endl;
        cin >> a;
        if (a == 3)break;
        switch (a)
        {
        case 1:
            cout << "输入起点和终点编号" << endl;
            cin >> i >> j;
            aa.enquiry_path(aa.p[i-1], aa.p[j-1]);
            break;
        case 2:
            cin >> i;
            aa.enquiry(i-1);
            break;
        default:
            break;
        }
    }
    return 0;
}