牛客欢乐赛1 E题

Posted 2021-06-15 zjj0624

题意


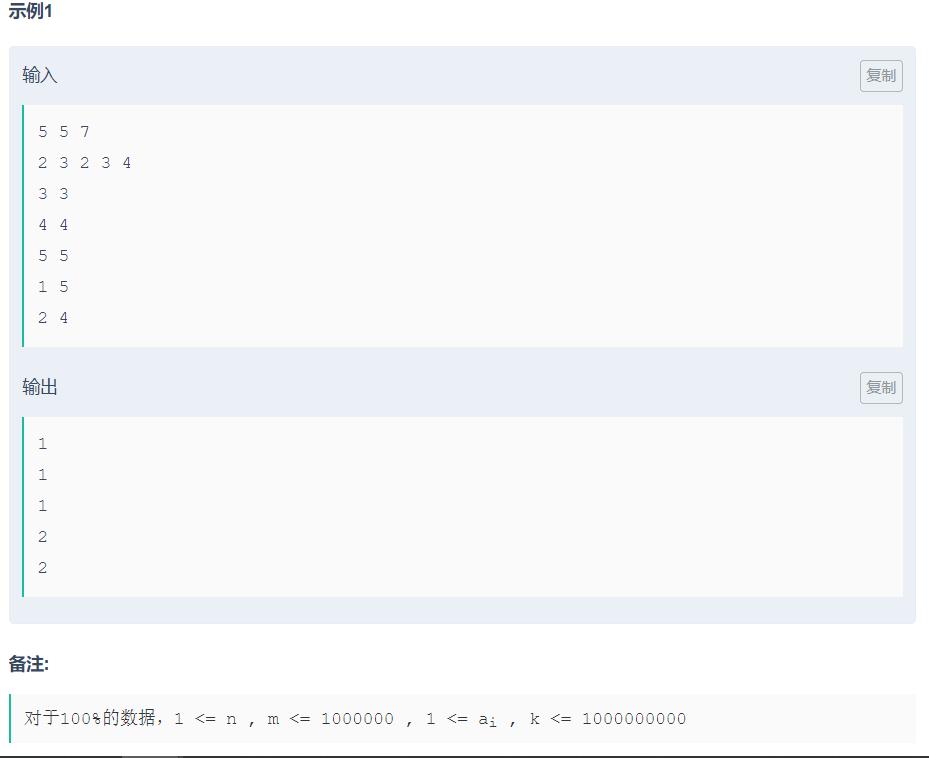
思路
首先我们拿到这个题肯定想到的是暴力，也就是每次给一个区间[L,R],我们就枚举区间L,R，然后看需要分多少个段，这样的事件复杂度肯定是会超时的。
我们可以用二分+前缀和的方式枚举出每个点能取的最大右端点是什么，然后每次求[L，R]的时候就不用每个点都需要枚举，而是直接可以一个区间一个区间的去看。
这样的话其实是可以被卡成和暴力时间复杂度一样的，假如每个区间都只有一个值的话，那我们每次枚举的区间也就每次是一个值，和第一种情况是一样的。
倍增
我们可以维护出一个st[I][j]表，这个数组的含义是
st[l][j]是从点i能取到$2^j$个区间的点，每个区间都是刚好小于等于k。
维护出来以后，我们就可以在log（n）的时间内查询，这个st表的预处理是nlog（n）,这样的复杂度下是可以解决的。
代码

#include <bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define me memset
const int N = 1e6+10;
const int MOD = 1e9+7;
const int INF = 0x3f3f3f3f;
using namespace std;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
int n,m,k;
int a[N],vis[N],st[N][21];
ll ss[N];
int solve(int l,int r)
{
    int ans=1;
   // cout<<l<<" "<<0<<" "<<st[l][0]<<endl;
    for(int i=20 ; st[l][0]<=r ; i--)
    {
        if(st[l][i]!=0&&st[l][i]<=r) l=st[l][i],ans+=(1<<i);
    }
    return ans;
}
int main()
{
    cin>>n>>m>>k;
    for(int i=1 ; i<=n ; i++)
    {
        cin>>a[i];
        ss[i]=ss[i-1]+a[i];
        if(a[i]>k) vis[i]=vis[i-1]+0;
        else vis[i]=vis[i-1]+1;
    }
    for(int i=1 ; i<=n ; i++)
    {
        st[i][0]=upper_bound(ss+1,ss+1+n,ss[i-1]+k)-ss;
        //cout<<i<<" "<<st[i][0]<<endl;
    }
    for(int i=1 ; (1<<i)<=n ; i++)
    {
        for(int j=1 ; j+(1<<i)<=n ; j++)
        {
            st[j][i]=st[st[j][i-1]][i-1];
        }
    }
    while(m--)
    {
        int l,r;
        cin>>l>>r;
        if(vis[r]-vis[l-1]<(r-l+1))
        {
            cout<<"Chtholly"<<endl;
            continue;
        }
        cout<<solve(l,r)<<endl;
    }
    return 0;
}