洛谷-----P1192 台阶问题

Posted 2021-06-15 大忽悠爱忽悠

台阶问题题解集合

• 记忆化DFS
• 动态规划

---

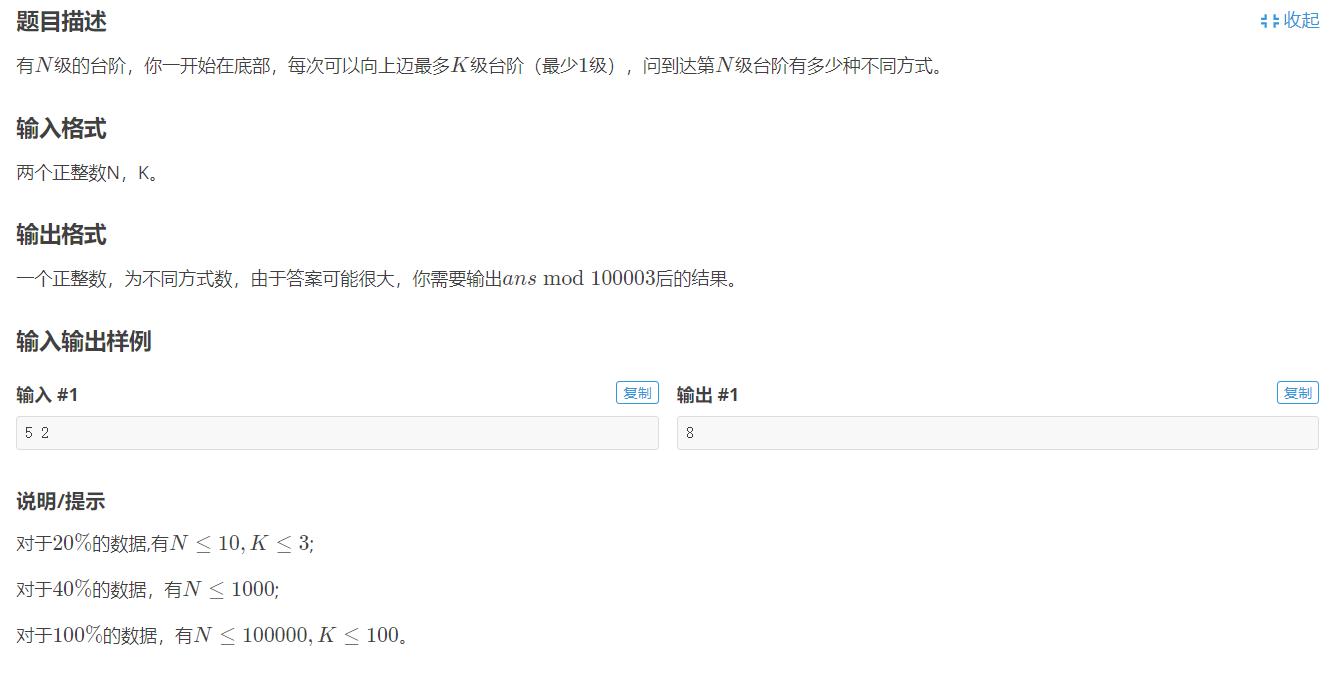
记忆化DFS

思路:

画出树形图，其实就是多k叉树的遍历，因为下面图中所举的例子中k=2,因此是对二叉树的遍历累加求和

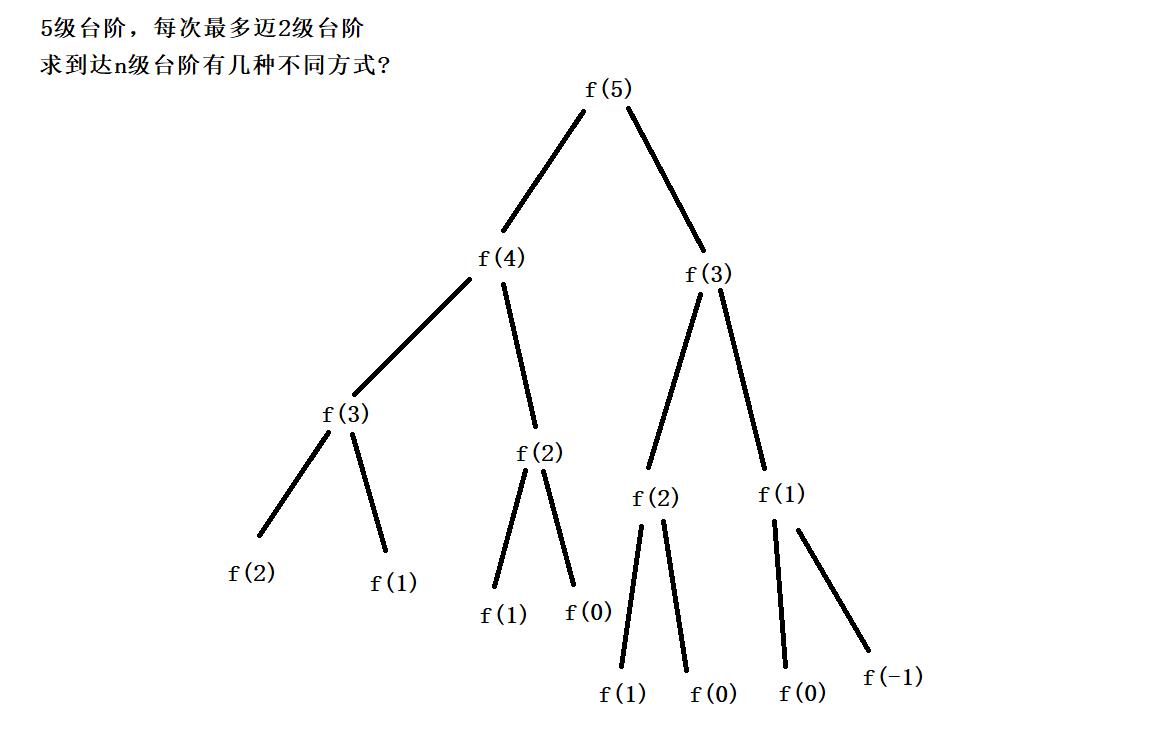
重复计算问题:

这里圈出来的并不是所有的重复计算，只是一部分，可见对于小数据来说，就有大量重复计算，那么对于海量数据而言，重复计算的数据量可想而知

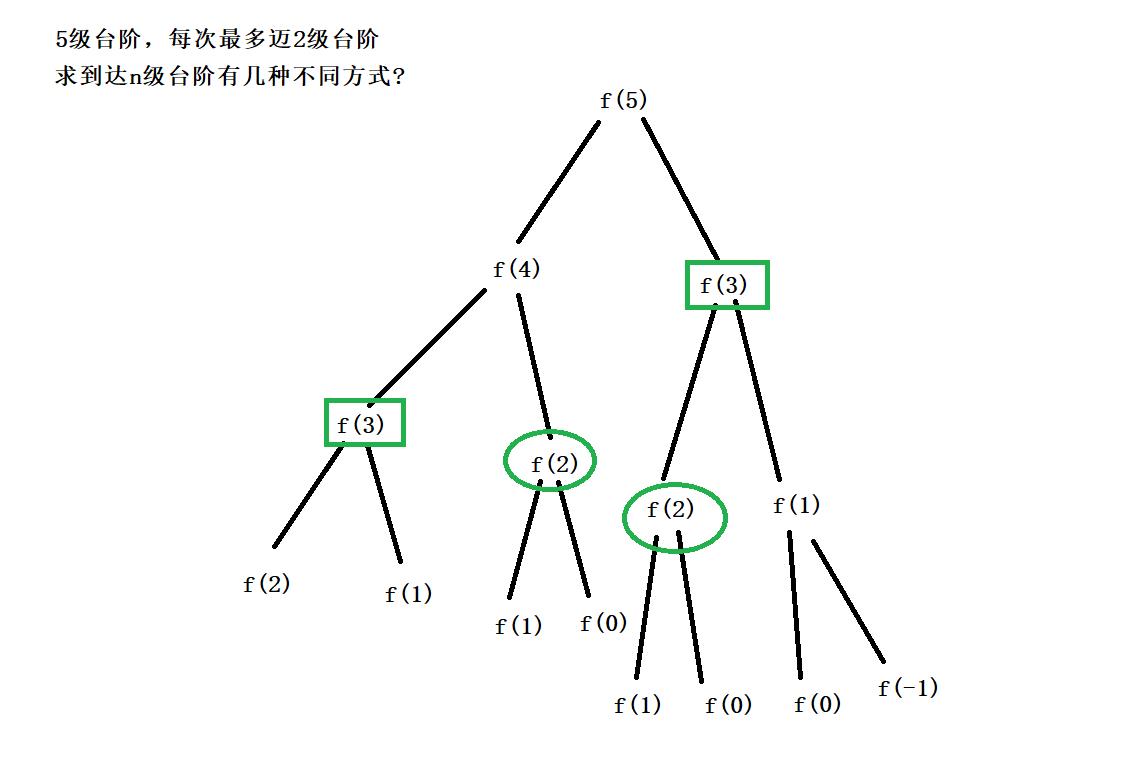
这里采用记忆化递归，即用一个哈希表保存已经计算出来的结果，避免重复计算

代码:

#include<iostream>
using namespace std;
#include<unordered_map>
class Solution {
	unordered_map<int, int> cache;
	int mod = 100003;
public:
	int solution(int N,int K)
	{
		if (cache.find(N) != cache.end()) return cache[N];
		//对于一级台阶，爬法总数为1
		//这里还需要考虑0级台阶的，爬法总数也为1
		if (N == 1||N==0) return 1;
		int sum = 0;
		for (int i = 1; i <= K&&N-i>=0; i++)
			sum =(sum+solution(N-i,K))%mod;
		return cache[N] = sum%mod;
	}
};
int main()
{
	Solution s;
	int N = 0, K = 0;
	cin >> N >> K;
	cout<<s.solution(N, K)<<endl;
	return 0;
}

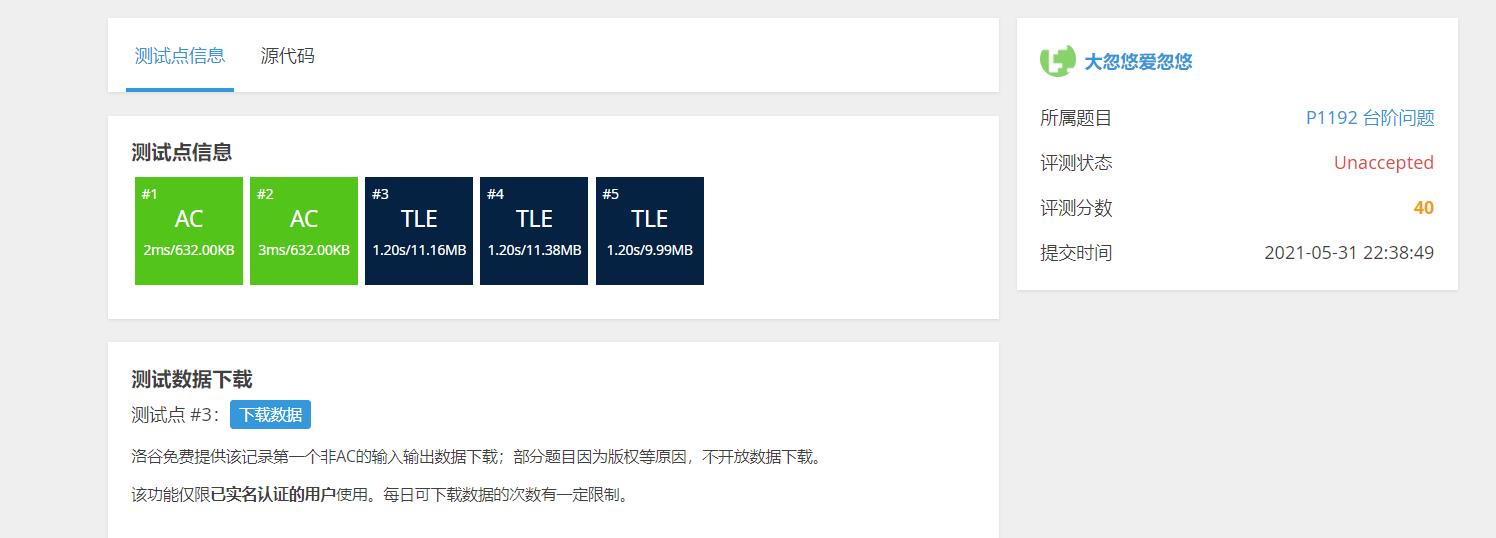
但是本题记忆化也不给过，那就只能考虑别的法子了

---

动态规划

根据下面的解空间树，我们可以看出dp[5]=dp[4]+dp[3], dp[4]=dp[3]+dp[2]…

由此推出状态转移方程:dp[n]=dp[n-1]+dp[n-2]+…dp[n-k]

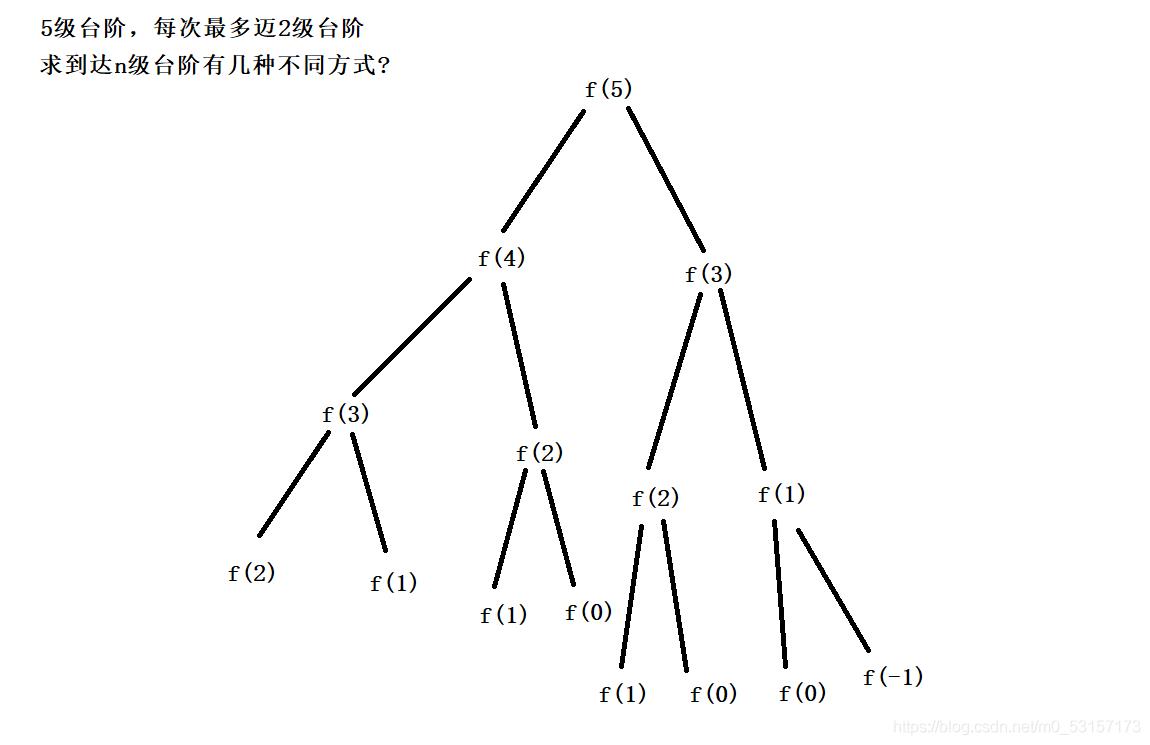
这里dp[i]的含义就是:当前i级台阶的走法总数

由记忆化解法可以得出，dp初始化为dp[0]=dp[1]=1

代码:

#include<iostream>
using namespace std;
#include<vector>
class Solution {
	int mod = 100003;
public:
	int solution(int N,int K)
	{
		vector<int> dp(N+1,0);
		dp[0] = dp[1] = 1;
		for (int i = 2; i <= N; i++)
		{
			for (int k = 1; k <= K&&i-k>=0; k++)
				dp[i] = (dp[i]+dp[i - k])%mod;
		}
		return dp[N]%mod;
	}
};
int main()
{
	Solution s;
	int N = 0, K = 0;
	cin >> N >> K;
	cout<<s.solution(N, K)<<endl;
	return 0;
}