890. 能被整除的数 容斥定理

Posted 2021-06-14 幽殇默

不得不说容斥定理真的好秒啊

https://www.acwing.com/problem/content/description/892/

先看一个例子:

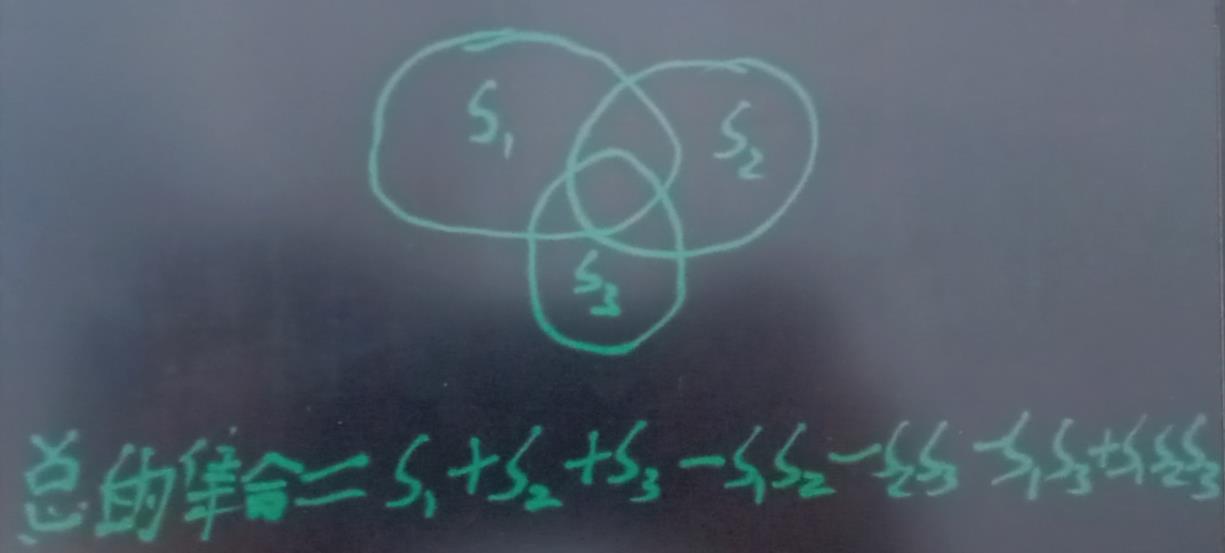
你会发现奇数集合构成的整体我们是加的，偶数集合构成的整体我们是减的。

总的扩展如下所示：

公式摘自：https://www.acwing.com/solution/content/29702/
回到本题，n中可以整除p的个数如下所示：

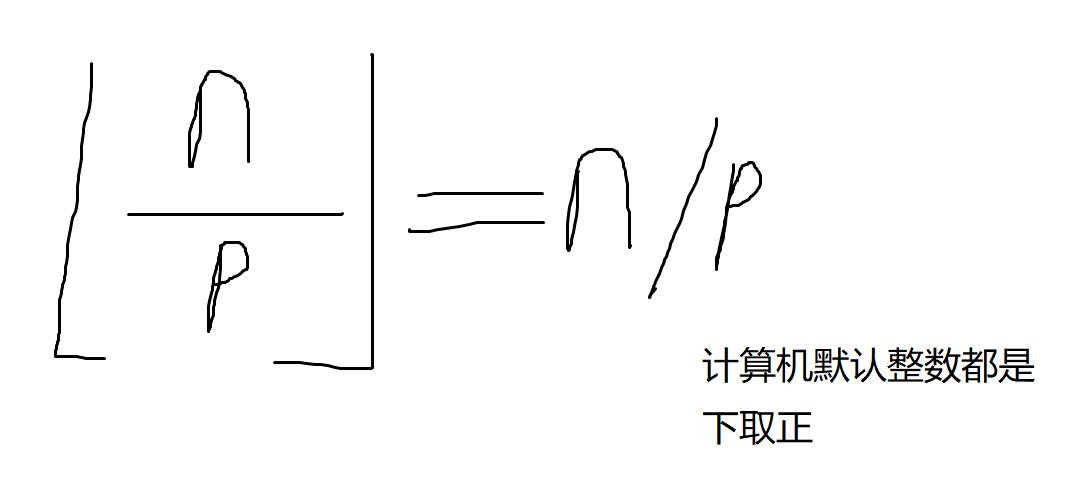
那么如何求一个交集的数的个数呢？
例： n中 同时可以整除 p1 和 p2 的个数。

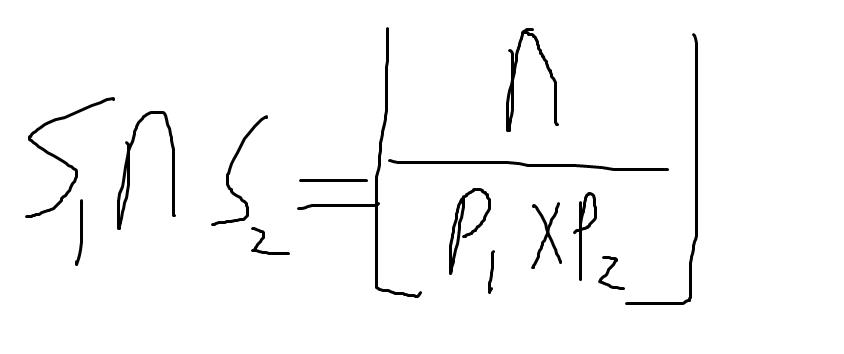
那么我们如何来求出本题中所有的集合的各个大小呢？

首先集合个数：

因为这里最少要选一个故总的集合数量是 2^m-1

你会发现这不就是对于每一个数选或不选的问题么？用二进制来表示所有的状态，其中1表示选了，0表示没有选。

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long int LL;
const int N=20;
LL p[N];
int main(void)
{
	LL n,m; cin>>n>>m;
	
	for(int i=0;i<m;i++) cin>>p[i];
	
	LL res=0;//统计结果
	
	for(int i=1;i<1<<m;i++)
	{
		LL t=1,s=0;
		for(int j=0;j<m;j++)
		{
			if(i>>j&1)//判断当前为不是不1
			{
				if(t*p[j]>n)//大于n故一个都没有
				{
					t=-1;
					break;
				}
				t*=p[j];
				s++;//统计1的个数
			}
		}
		
		if(t!=-1)
		{
			if(s%2) res+=n/t;//奇数是加
			else res-=n/t;//偶数是减
		}
	}
	
	cout<<res<<endl;
	return 0;
}