图卷积网络GCN

Posted Facico

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了图卷积网络GCN相关的知识，希望对你有一定的参考价值。

GCN

  • CNN中的卷积本质上就是共享参数的过滤器，可以较为有效地提取空间特征

而很多其他的研究中还有很多非欧拉结构的数据
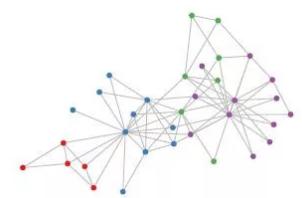
在这里插入图片描述

  • 1.CNN无法处理非欧拉结构的数据，传统的离散卷积在Non Euclidean Structure的数据上无法保持平移不变性
  • 2.希望在拓扑图上有效地提取空间特征来进行机器学习
  • 3.广义上来讲任何数据在赋范空间内都可以建立拓扑关联，因此GCN有很大的应用空间

提取拓扑图空间特征的两种方式

  • （1）vertex domain

    • 把顶点相邻的点找出来
    • 问题就变成：怎么确定相邻点，怎么确定感受野，确定感受野怎么处理包含不同数目的相邻点的特征
    • 相关的文章Convolutional Neural Networks for Graphs

  • （2）spectral domai

    • 希望用图谱的理论来实现卷积操作

拉普拉斯矩阵

定义一个图的Laplacian矩阵 L = D − A L=D-A L=D−A

  • L表示拉普拉斯矩阵
  • D是顶点的度矩阵（对角矩阵，对角线上为图顶点的度）
  • A是图的邻接矩阵

常用的Laplacian矩阵有三种

  • 1. L = D − A L=D-A L=D−A

  • 2. L s y s = D − 1 / 2 L D − 1 / 2 L^{sys}=D^{-1/2}LD^{-1/2} Lsys=D−1/2LD−1/2，很多GCN使用

  • 3. L r w = D − 1 L L^{rw}=D^{-1}L Lrw=D−1L

  • 矩阵的谱分解、特征分解、对角化是同一个概念，充要条件是n阶方阵存在n个线性无关的特征向量
    在这里插入图片描述

    • 这里的特征值可以表示为频率
      • 由Graph确定的n维空间中，越小的特征值 λ l \\lambda_l λl​表明：拉普拉斯矩阵L其所对应的基 u l u_l ul​上的分量信息越少，类似PCA降维里的原理

拉普拉斯算子与其关系

  • 代数里拉普拉斯算子是一个二阶微分算子

nabla算子
∇ = ∂ ∂ x i ⃗ + ∂ ∂ y j ⃗ + ∂ ∂ z k ⃗ \\nabla = \\frac{\\partial}{\\partial x}\\vec i+\\frac{\\partial}{\\partial y}\\vec j+\\frac{\\partial}{\\partial z}\\vec k ∇=∂x∂​i +∂y∂​j ​+∂z∂​k

拉普拉斯算子
Δ f = ∂ 2 ∂ x 2 i ⃗ + ∂ 2 ∂ y 2 j ⃗ + ∂ 2 ∂ z 2 k ⃗ \\Delta f = \\frac{\\partial^2}{\\partial x^2}\\vec i+\\frac{\\partial^2}{\\partial y^2}\\vec j+\\frac{\\partial^2}{\\partial z^2}\\vec k Δf=∂x2∂2​i +∂y2∂2​j ​+∂z2∂2​k

以二维的离散函数为例
Δ f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \\Delta f = \\frac{\\partial^2 f}{\\partial x^2}+\\frac{\\partial^2 f}{\\partial y^2}\\\\ = f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) Δf=∂x2∂2f​+∂y2∂2f​=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
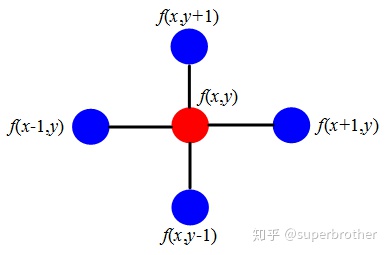在这里插入图片描述- 所以拉普拉斯算子可以计算一个点到它所有自由度上微小扰动的增益

将2维推广到n维，即是在一张图中计算某点邻域的扰动
设对节点i的增益： Δ f i = ∑ j ∈ N i ( f i − f j ) \\Delta f_i = \\sum_{j\\in N_i}(f_i-f_j) Δfi​=∑j∈Ni​​(fi​−fj​)
带边权则有
Δ f i = ∑ j ∈ N i w i j ( f i − f j ) = ∑ j ∈ N w i j f i − ∑ j ∈ N w i j f j = d i f i − w i : f \\Delta f_i = \\sum_{j\\in N_i}w_{ij}(f_i-f_j)\\\\ =\\sum_{j\\in N}w_{ij}f_i-\\sum_{j\\in N}w_{ij}f_j\\\\ =d_if_i-w_{i:}f Δfi​=j∈Ni​∑​wij​(fi​−fj​)=j∈N∑​wij​fi​−j∈N∑​wij​fj​=di​fi​−wi:​f