虹科教您 | 实时频谱分析仪中如何选择合适的FFT窗函数

Posted 2021-06-09 weixin_43123641

虹科

本文主要介绍了常见的窗函数以及窗函数有什么用，以及在实时频谱分析中，该如何选择合适的加窗方式。

随着无线通信的逐步发展，带来的是频谱环境的越发复杂与丰富，高度的信号变化性使得短时间内信号不再是一成不变。低功率、瞬时性、宽频带的特性使得传统的扫频式频谱分析仪有所局限。以目前火热的UWB定位技术来讲，发射能量往往低于-40 dBm/MHz，UWB不使用载波，而是使用短的能量脉冲序列（ns级以下），频域上带宽很宽，因此如果想要观测解析这样的信号，对于扫频仪来讲就分外吃力。

因此，实时频谱分析仪逐渐占据了市场。而实时频谱分析仪需要面对的信号依旧是有挑战性的，为了能够适应不同的信号，实时频谱分析仪在FFT的加窗类型中会给出不同的窗函数，以便在需要的时候为用户提供了扩展分析能力。

但是很多时候，多种多样的窗函数会让人感到迷惑，并不知道针对自己需要观测的信号，该如何进行选择，本文将从常见窗函数的角度出发，用尽可能直观的方式解读如何为频谱分析仪选择合适的加窗方式。

为什么使用窗函数？

HONGKE
首先我们要清楚，数字信号处理（DSP）中很重要的一个内容，也是承载数模转换的基础部分是傅立叶变换（Fourier Transform）。从傅里叶实现的机制来看，傅里叶变换都是针对正无穷大和负无穷大的信号，即信号的的长度是无穷大的，但是这对于计算机处理来说是不可能完成的，那么有没有针对长度有限的傅里叶变换呢？没有。因此，为了让计算机实现FFT，就必须将无线信号截取成一段有限长的信号后进行周期延拓，再进行傅立叶变换。

在这个过程中，当截断时间不等于周期或周期的整数倍时，此时截断后再延拓时，幅值不连续，FFT时频转换之后的频带就将出现拖尾，此时我们就可以称为频谱能量泄露，幅度峰值下降，频谱扩散。
很不幸的是，现实世界的操作中，大多数信号在截取时最终都是非周期截取，因此泄露是在计算机执行FFT的过程中很常见的一个现象。

窗函数就是为了解决这个问题而出现的，顾名思义，窗函数就是时域上一个宽度有限的信号起到了对无限信号进行截断的作用，使得FFT过程仅仅能处理截断后“窗户”内的信号。通过合理的窗函数进行截断，可以有效的减少泄露，需要强调的是，只要是进行了截断，就必然会产生泄露，窗函数只是减少了泄露而做不到完全的消除。

有哪些窗函数？

HONGKE
正如上文所说，窗函数实际上就是一个截取工具，用来将时域信号“框”起来一部分，再“展示”给FFT函数来进行处理，下面是一个例子：

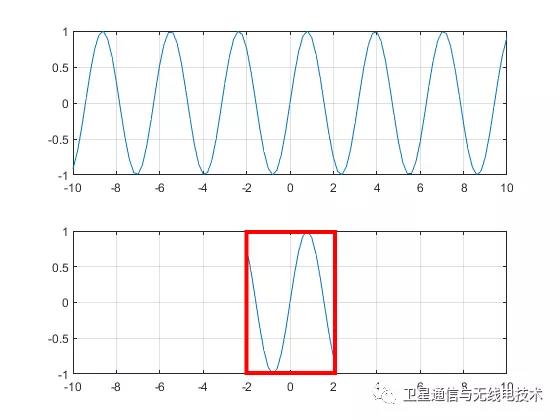
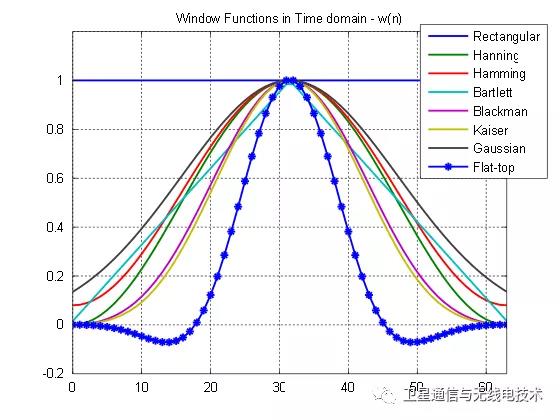
因此从这一点来看，所有的窗函数都具有相同的功能。不同的窗函数具有不同的频谱特征，如何来对这些不同的窗函数做对比与定义呢？

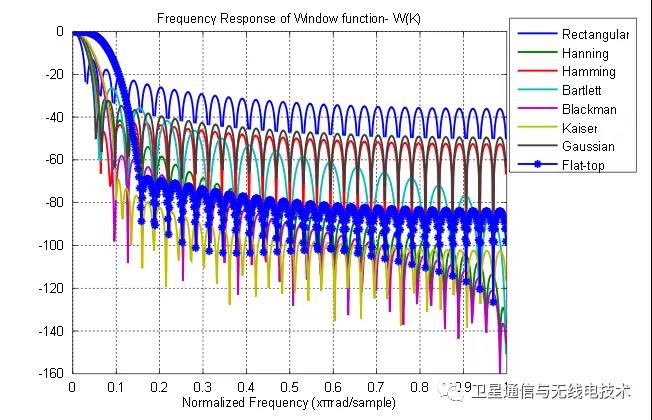
上图是几种窗函数在频域的图像，可以看到实际上尽管这些窗函数在时域上有不同的形态，但是从频域的角度来看，我们都认为它具有较清晰的主瓣和旁瓣区别。尽管截取这一过程比较直观的发生在时域，但是泄漏与窗函数的频谱特征相关的，从频谱特征能够更方便的进行解释：

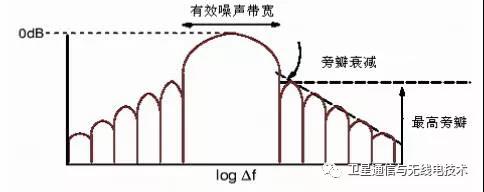
上图是窗函数的典型频谱特征图，我们提取了这样几个频域特征作为衡量不同窗函数之间的性能指标：最高旁瓣、主瓣等效噪声带宽、3dB带宽、旁瓣衰减。
实时频谱分析仪应用的窗函数有哪些呢？我们以虹科模块化实时频谱分析仪和D4卫星载波检测频谱分析仪为例，来介绍几种较为常用的窗函数：
Rectangular（矩形窗）：主瓣比较集中，缺点是旁瓣较高，并有负旁瓣，导致变换中带进了高频干扰和泄漏，甚至出现负谱现象

• Flattop（平顶窗）：主瓣稍宽，幅度的准确性更高

• Blackman-Harris（布莱克曼窗）：是一种类似于汉明窗与汉宁窗的窗函数，但是主瓣宽，旁瓣小，频率识别精度最低，但幅值识别精度最

• Hamming（汉明窗）：是一种改进的升余弦窗，旁瓣较汉明窗来讲更小，频率分辨率高

• Hanning（汉宁窗）：升余弦窗，汉宁窗可以看作是3个矩形时间窗的频谱之和，它可以使用旁瓣互相抵消，消去高频干扰和漏能。

  各种窗的差别主要在于集中于主瓣的能量和分散在所有旁瓣的能量之比，而主瓣的集中度与旁瓣的衰减程度决定着频率分辨率与幅值精度，我们对各个窗进行了总结：

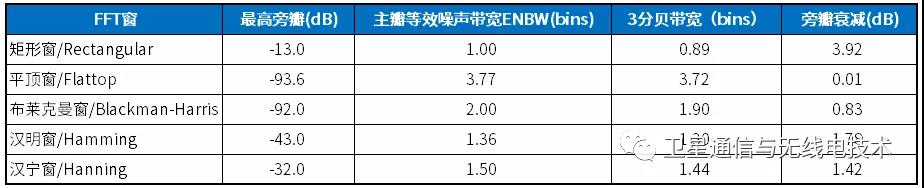
为什么使用窗函数？

我们在加窗函数时，最理想的情况是使窗函数频谱的主瓣宽度应尽量窄（频率分辨率高），旁瓣衰减应尽量大（频谱拖尾小）但实际上我们需要做一个选择题。“鱼与熊掌不可兼得”，这两个参数处在跷跷板的两端，我们在加窗时只能更顾及其中一点。
因此，对于窗函数的选择，我们应考虑被分析信号的性质与自身的处理需求。
如果仅要求精确读出主瓣频率，而不考虑幅值精度，则可选用主瓣宽度比较窄而便于分辨的矩形窗，例如测量物体的自振频率等；
如果分析窄带信号，且有较强的干扰噪声，则应选用旁瓣幅度小的窗函数，如汉宁窗、三角窗等；
对于随时间按指数衰减的函数，可采用指数窗来提高信噪比。
我们总结了各个窗函数的特性与应用场合：

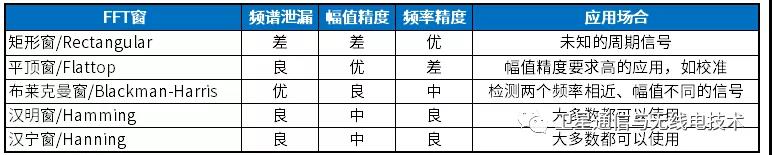
在我们日常使用频谱仪时，窗函数的选择对于最终测试影响不会特别大，因此无须刻意纠结选取哪一种来使用，当我们需要准确的结果时，可以参照上表，根据自身需求进行设置，这在一定程度上会保证测量的精度与准确度。