FFT频谱分析（补零频谱泄露栅栏效应加窗细化频谱混叠），MatlabC语言代码

Posted 2021-12-28 “逛丢一只鞋”

文章目录

• 引言
• Matlab FFT函数
• 频谱混叠
• 栅栏效应
• 细化技术
• • 什么是细化技术?
  • 细化FFT技术的应用：
  • Zoom-FFT算法介绍及MATLAB实现
  • Zoom-FFT根本没有实现“细化“？
  • 到底该怎么实现“细化”?
• 补零
• • 补零对频谱的影响
  • 补零与离散傅里叶变换的分辨率
  • 补零与插值对FFT的影响
• 频谱泄露
• • 信号的截断
  • 频谱泄露定义
• 窗
• • 窗的概念
  • • 常用窗函数
    • 如何选择“窗函数”？
  • 频谱泄漏的原因
  • 加窗应用（汉宁窗）
  • 加窗对频率和幅值的影响
• FFT变换的幅值和能量校正
• • 幅值修正谱
  • 能量修正谱
  • 转换的比例因子关系

引言

在对信号进行谐波分析的过程中，对时域信号进行FFT之后发现时域中本来相同幅值的信号分量，在频域中频率点正确，但是频域幅值却出现了不同，因此对此现象进行分析的探讨

此FFT的频率分辨率为0.36，后续通过增加采样点的方式将频率分辨率提升到0.18，但是仍然出现频域幅值不一致的现象。

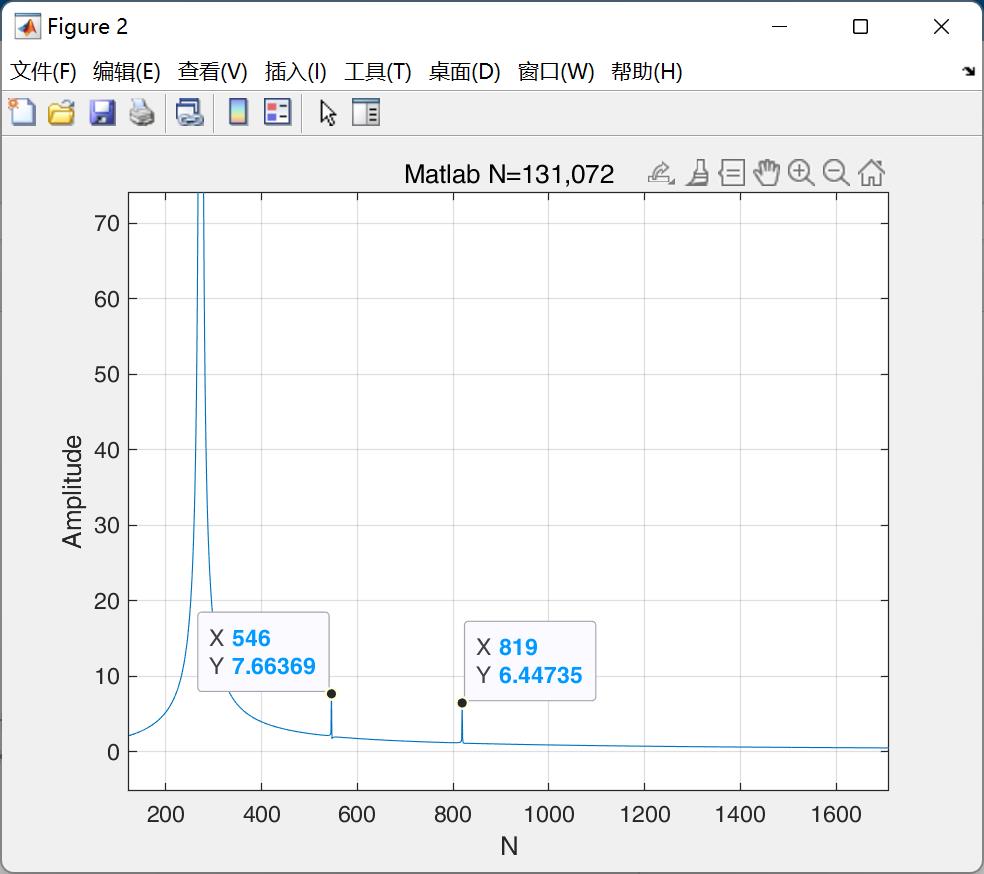
接着FFT过程中的疑问，本文收集了FFT过程中涉及到的 补零、频谱泄露、栅栏效应、加窗、细化、频谱混叠 等概念，尝试对上述出现的问题进行答案的寻找

最终以实现频域与时域更加精确的对照

Matlab FFT函数

首先说明一下，用MATLAB做FFT并不要求数据点个数必须为以2为基数的整数次方。之所以很多资料上说控制数据点数为以2为基数的整数次方，是因为这样就能采用以2为基的FFT算法，提升运算性能。

如果数据点数不是以2为基数的整数次方，处理方法有两种

一种是在原始数据开头或末尾补零，即将数据补到以2为基数的整数次方，这是“补零”的一个用处；

第二种是采用以任意数为基数的FFT算法。

而MATLAB的[公式]函数在参数[公式]正好就是数据[公式]的长度，但又不是以2为基数的整数次方时，并不会采用补零的方法，而应该是采用以任意数为基数的FFT算法（说“应该”是因为帮助文档里没有明确说明），这样也能得到很好的结果，只不过速度要稍稍慢了一些，以通常的计算量是体现不出来的。

频谱混叠

定义：一般原因时域信号采样离散化时，采样频率fc不满足奈奎斯特采样定理：fc>=2*fmax

奈奎斯特采样定理：模数转换时，采样频率fc符合这个定理，就能采出合适的信号，采的的离散信号无论是从时域还是频域都可以很好的恢复原信号。

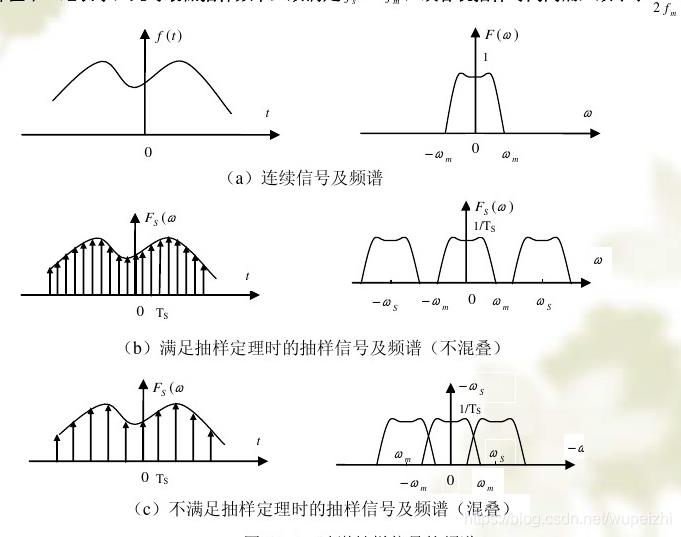
奈奎斯特定理已被众所周知了，所以几乎所有人的都知道为了不让频谱混叠，理论上采样频谱大于等于信号的最高频率。

了解了概念，那和时域上联系起来的关系是什么呢？

设定采样点数为 N，采样频率 fs，最高频率 fh，故频谱分辨率 f = fs / N,而 fs >= 2fh，所以可以看出最高频率与频谱分辨率是相互矛盾的，提高频谱分辨率f的同时，在 N 确定的情况下必定会导致最高频率 fh 的减小；同样的，提高最高频率 fh 的同时必会引起f的增大，即分辨率变大。

栅栏效应

在进行DFT的过程中，最后需要对信号的频谱进行采样。经过这种采样所显示出来的频谱仅在各采样点上，而不在此类点上的频谱都显示不出来，即使在其他点上有重要的峰值也会被忽略，这就是栅栏效应。

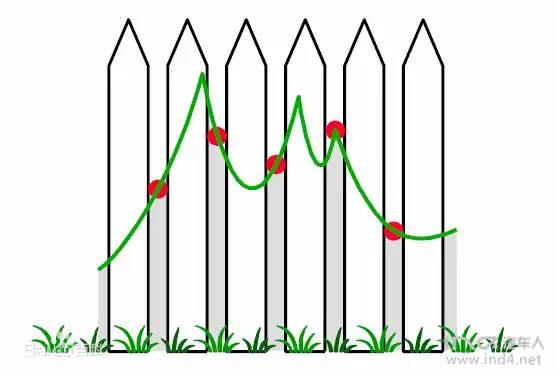
这一效应对于周期信号尤为重要，因其频谱是离散的，如处理不当这些离散谱线可能不被显示。

不管是时域采样还是频域采样，都有相应的栅栏效应。只是当时域采样满足采样定理时，栅栏效应不会有什么影响。而频域采样的栅栏效应则影响很大，“挡住”或丢失的频率成分有可能是重要的或具有特征的成分，使信号处理失去意义。

减小栅栏效应可用提高采样间隔也就是频率分辨力的方法来解决。间隔小，频率分辨力高，被“挡住”或丢失的频率成分就会越少。但会增加采样点数，使计算工作量增加。

解决此项矛盾可以采用如下方法：在满足采样定理的前提下，采用频率细化技术(ZOOM），亦可用把时域序列变换成频谱序列的方法。

在对周期信号DFT处理时，解决栅栏效应应以致解决泄露效应的一个极为有效的措施是所谓“整周期截取”。

而对于非周期信号，如果希望减小栅栏效应的影响，尽可能多地观察到谱线，则需要提高频谱的分辨率。

细化技术

在解决栅栏效应中，碰到了一个概念，叫做细化，对与本设计中出现的问题，因为频率分辨率最后已经达到了0.36，频率点也都比较准确，所以出现栅栏效应的可能性较小。

但是，对于栅栏效应和细化技术，还是很值的去探索一下

也对 Zoom-FFT算法 进行一个学习

什么是细化技术?

**细化技术是一种一定频率范围内提高频率分辨率的测量技术，也叫细化傅里叶分析。**即在所选择的频带内，进行与基带分析有同样多的谱线的分析。从而能大大提高频率分辨率。

选带分析时频率分辨率为：

选带傅氏分析（细化）的主要步骤是：

(a) 输入信号先经模拟抗混滤波，滤去所需分析的最高频率即基带分析中的最高分析频率以上的频率成分；

(b) 经过模数转换，变为数字信号序列；

© 将采样信号经数字移频，移频后的Fk处的谱线将落在频率轴上的零频处；

(d) 将移频后的数字信号再经数字低通滤波，滤去所需频带以外的信号；

(e) 对滤波后的信号的时间序列进行重采样，此时分析的是一段小频段为原来的1/M。这样在一小频段上采样，采样量还是N，但采样时间加了M倍，提高了分辩率。

细化FFT技术的应用：

一些不能增加总的采样点数而分辨率又要求精细的场合，细化FFT分析是很有用的。例如：

（a）区分频谱图中间距很近的共振尖峰，用常规分析不能很好分开时，用细化分析就能得到满意的结果。

（b）用于增加信噪比，提高谱值精度，这是由于细化时采用了数字滤波器，混叠与泄漏产生的误差都非常小;

（c ) 用于分离被白噪声淹没的单频信号，由于白噪声的功率谱与频率分辨率有关，每细化一个2倍，白噪声的功率谱值降低3dB，若细化256倍，白噪声功率谱值即下降24 dB，而单频信号的谱线就会被突出出来。

Zoom-FFT算法介绍及MATLAB实现

下面对该方法进行仿真，仿真参数如下

参数值	参数名称
采样频率	1000Hz
细化倍数	50
滤波器阶数	200
FFT点数	2048
频率	166.4Hz、165Hz

下面对该方法进行仿真，仿真参数如下

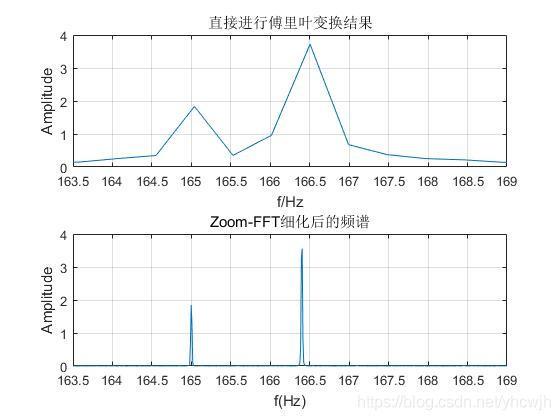
从图中可以看出，直接进行FFT，频率与原始频率有些许误差，并且不是很能分辨，但是细化后的频谱能够很好地区分信号的频率，很准确地得到了信号的频率。

clear;
close all;
clc;
fs=1000;   %采样频率
N=2048;    %傅里叶变换点数
D=50;      %细化倍数
M=200;     %滤波器阶数

t=(0:N*D+2*M)/fs;    %时间轴
x=4*sin(2*pi*166.4*t)+2*sin(2*pi*165*t+pi/6)...
    +0.6*randn(1,N*D+2*M+1);  %信号

xf=fft(x,N);     %傅里叶变换
xf=abs(xf(1:N/2))/N*2;
subplot(211);
plot((0:N/2-1)*fs/N,xf);
axis([163.5 169 0 4])
grid on
xlabel('f/Hz');ylabel('Amplitude')
title('直接进行傅里叶变换结果')


% 细化

fe=167;     %中心频率

k=1:M;                          
w=0.5+0.5*cos(pi*k/M);          %Hanning函数

fl=max(fe-fs/(4*D),-fs/2.2);    %频率下限
fh=min(fe+fs/(4*D),fs/2.2);     %频率上限

yf=D*fl; 
df=fs/D/N;        %分辨率
f=fl:df:fl+(N/2-1)*df;
xz=zeros(1,N/2);
wl=2*pi*fl/fs;    %归一化角频率
wh=2*pi*fh/fs;
hr(1)=(wl-wh)/pi;
hr(2:M+1)=(sin(wl*k)-sin(wh*k))./(pi*k).*w;
hi(1)=0;
hi(2:M+1)=(cos(wl*k)-cos(wh*k))./(pi*k).*w;

p=0:N-1;
w=0.5-0.5*cos(2*pi*p/N);
xrz=zeros(1,N/2);
xiz=zeros(1,N/2);
L=10;   %循环次数
for i=1:L
    for k=1:N
        kk=(k-1)*D+M;
        xrz(k)=x(kk+1)*hr(1)+sum(hr(2:M+1).*(x(kk+2:kk+M+1)+x(kk:-1:kk-M+1)));
        xiz(k)=x(kk+1)*hi(1)+sum(hi(2:M+1).*(x(kk+2:kk+M+1)-x(kk:-1:kk-M+1)));
    end
    xzt=(xrz+1j*xiz).*exp(-1j*2*pi*(0:N-1)*yf/fs);
    xzt=xzt.*w;
    xzt=xzt-sum(xzt)/N;
    xzt=fft(xzt);
    xz=xz+(abs(xzt(1:N/2))/N*2).^2;
end
xz=(xz./L).^0.5;
subplot(212);
plot(f,xz);
axis([163.5 169 0 4])
grid on
xlabel('f(Hz)');ylabel('Amplitude')
title('Zoom-FFT细化后的频谱')

Zoom-FFT根本没有实现“细化“？

首先说频率分辨率的概念，默认指的信号客观的物理可达到的分辨率，即物理分辨率；并非“计算分辨率”

假设信号的采样时间Delta_T定了，信号在频域上的理论最高分辨率也就已经确定了，等于Delta_f=1/Delta_T;

如下信号及其对应频谱


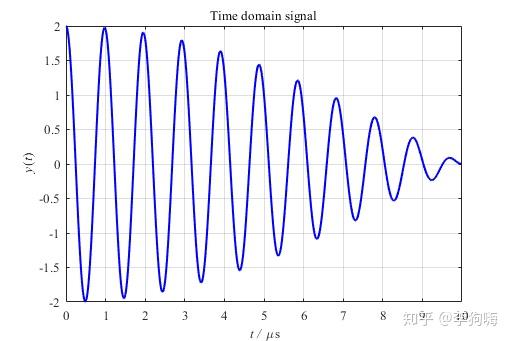
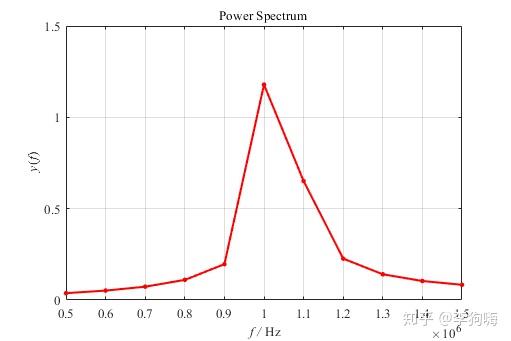
通过细化的原理我们可以知道，本质上为选择一个频带范围，针对这个频带进行补零的操作，时域中补零之后，我们可以看到，频谱点密集了不少

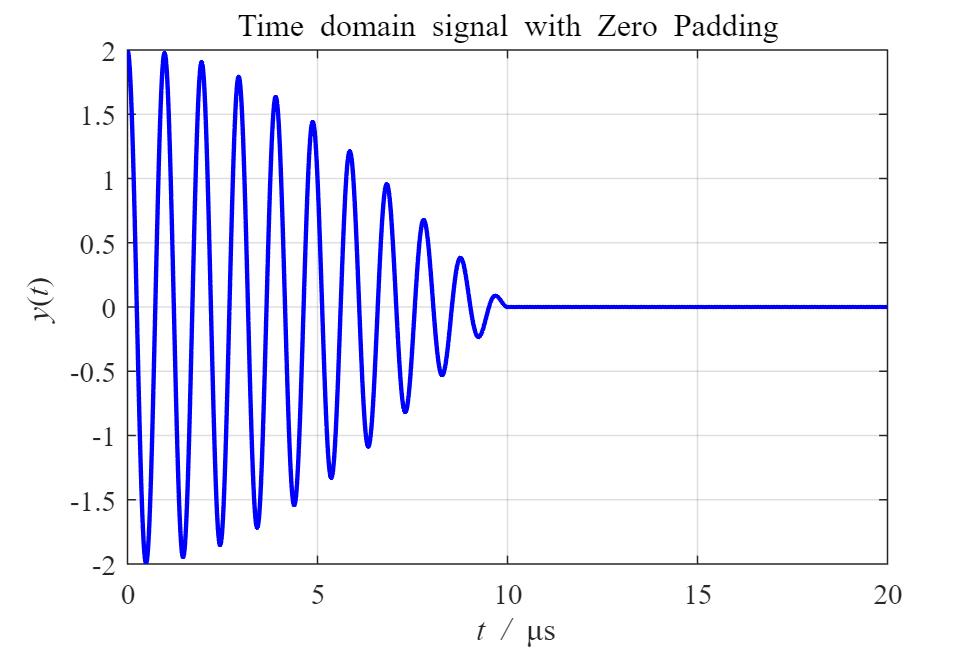
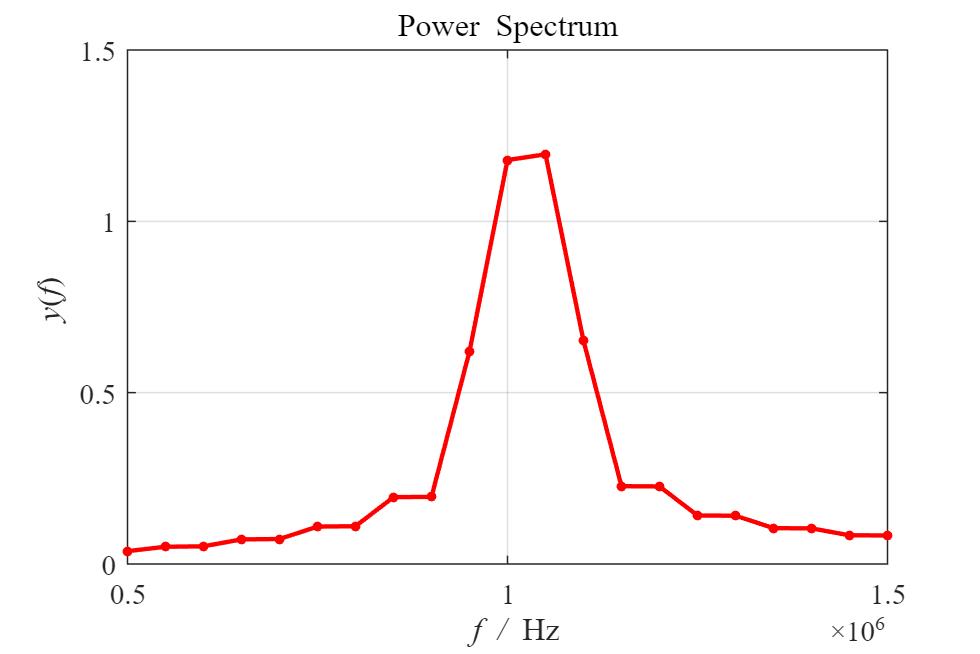
通过上述的一个对比，我们可以非常直观的得到结论，如果你把信号补一倍长度的0，可以计算出一个分辨率为0.5*Delta_f的频谱，但这对信号分析没有增加新的物理信息，其实仅仅是数学游戏；增加的是“计算分辨率”，没有增加任何“物理分辨率”。

再说什么是细化。

所谓细化，我认为定义应该是：（不增加信号时域长度的情况下），提高其频谱分析物理分辨率的操作。

ZoomFFT，实现时，如果细化为原来的D倍,变为Delta_f/D；则要求采样长度相应的也应该是原来的D倍，D*N；

而既然如此，直接经FFT得到的频谱，其实分辨率本身就是Delta_f/D。ZoomFFT所做的， 只不过直接FFT计算点数是D*N，ZoomFFT通过巧妙的办法，使计算量仍旧是N；并且，只选取我们所关心的“频带”去计算。

对我们而言，我们也可以直接FFT得到频谱后，只绘制我们关心的那个“频带”；相对该直接FFT方法，在获得信息上ZoomFFT没有任何增加；仅仅提高了效率（连这其实都值得商榷，如果我们同时有关心其他频率，ZoomFFT还得重算）。

所以，我认为ZoomFFT的更确切的称呼，应该是“选带分析”，而非“细化分析”；当然这是沿用我理解的前面的细化的定义。

ZoomFFT这一“手段”，在高性能个人数字计算机普及之前的分析仪器时代，对性能的提高意义是十分巨大的，因为那时，哪怕做一组512点的FFT，耗时都是很可观的；但现在，意义已经不再如过去那么显著；毕竟，在PC机上，计算哪怕是较长的FFT已经都是ms-秒级的时间。

当然，目前来说ZoomFFT这一“手段”，对于存储量、计算能力相对弱的便携计算机/仪器而言，还是有意义的。补零确实不能提高客观实在的“物理分辨率”

可是好多振动信号处理领域的学者没有意识到这点。细化是针对FFT分析点数固定的情况下来说的.这在20年前计算机内存小,计算速度慢是有意义的,现在计算机速度快了.可以不用考虑细化技术了

但是，在FFT出现栅栏效应时，可以有弥补作用

到底该怎么实现“细化”?

我理解，除非对原始信号进行外推或者就是认为采时间上更长的信号，再经FFT得到频谱，否则无法实现真正的“细化”。

现代功率谱分析方法，隐含了对信号的外推，可以突破前述Delta_f=1/Delta_T的限制。

提高频率分辨率最实用的办法是采样更长时间的数据？

正确。

但是还要注意一个问题，采样数据不宜太长，太长的话，即使不考虑存储问题，直接通过FFT做出离散傅里叶频谱还会引起两方面问题：

1. DFT没有考虑到系统的时变特性，太长时间里时不变假设还能否成立是个问题
2. 分析线数过高，分辨率过高的话；有用信号在频域上分得过细，从测量的角度噪声就可以更加趁虚而入了。

刘馥清教授曾在LMS的培训会上谨慎地建议1600线就可以了，再高的话意义不是太大。

补零

对细化有了更深的了解之后，其实补零也就清晰了

补零对频谱的影响

进行zero padding只是增加了数据的长度，而不是原信号的长度。就好比本来信号是一个周期的余弦信号，如果又给它补了9个周期长度的0，那么信号并不是10个周期的余弦信号，而是一个周期的余弦加一串0，补的0并没有带来新的信息。

其实zero padding等价于频域的sinc函数内插，而这个sinc函数的形状（主瓣宽度）是由补0前的信号长度决定的，补0的作用只是细化了这个sinc函数，并没有改变其主瓣宽度。

而频率分辨率的含义是两个频率不同的信号在频率上可分，也就要求它们不能落到一个sinc函数的主瓣上。

所以，如果待分析的两个信号频率接近，而时域长度又较短，那么在频域上它们就落在一个sinc主瓣内了，补再多的0也是无济于事的。

补零与离散傅里叶变换的分辨率

离散傅里叶变换(DFT)的输入是一组离散的值，输出同样是一组离散的值。在输入信号而言，相邻两个采样点的间隔为采样时间Ts。在输出信号而言，相邻两个采样点的间隔为频率分辨率fs/N，其中fs为采样频率，其大小等于1/Ts，N为输入信号的采样点数。

这也就是说，DFT的频域分辨率不仅与采样频率有关，也与信号的采样点数有关。

那么，如果保持输入信号长度不变，但却对输入信号进行补零，增加DFT的点数，此时的分辨率是变还是不变？

答案是此时分辨率不变，增加0可以更细致观察频域上的信号，但不会增加频谱分辨率。

从时域来看，假定要把频率相差很小的两个信号区分开来，直观上理解，至少要保证两个信号在时域上相差一个完整的周期，也即是相位相差2*pi。

举个例子，假定采样频率为1Hz，要将周期为10s的正弦信号和周期为11s的正弦信号区分开来，那么信号至少要持续110s，两个信号才能相差一个周期，此时周期为10s的那个信号经历的周期数为11，而11s的那个信号经历的周期书为10。转化到频域，这种情况下，时域采样点为110，分辨率为1/110=0.00909，恰好等于两个信号频率只差（1/10-1/11）。如果两个信号在时域上不满足“相差一个完整周期“的话，补零同样也不能满足“相差一个完整周期”，即分辨率不发生变化。

另外，从信息论的角度，也很好理解，对输入信号补零并没有增加输入信号的信息，因此分辨率不会发生变化。

那么，补零到底会带来什么样的影响呢？因为DFT可以看做是对DTFT的采样，补零仅是减小了频域采样的间隔。这样有利于克服由于栅栏效应带来的有些频谱泄露的问题。也就是说，补零可以使信号能在频域被更细致地观察。如果不满足上述“至少相差一个完整周期”的要求，即便是如DTFT一般在频域连续，也无法分辨出两个信号。

那么，影响DFT分辨率最本质的物理机制是什么呢？在于DFT的积累时间，分辨率为积累时间T的倒数。这点从数学公式上可以很容易得到：

fs / N = 1 /（N * Ts）= 1 / T

举个例子说，如果输入信号的时长为10s，那么无论采样频率为多少，当然前提是要满足奈奎斯特定理，其分辨率为1/10=0.1Hz。

补零与插值对FFT的影响

我们常常在对序列进行FFT变换之前会进行补零或者插值操作，但是二者对FFT的影响我一直很模棱两可，现在结合频率分辨率与matlab仿真结果对两者的影响进行总结与分析。

仿真的代码如下：

% 看看插值和补零对FFT结果的影响。
clc
clear
% 采样频率
fs = 4000;
% 三个频率分量
f1 = 200;
f2 = 400;
f3 = 600;
% 采样800个点,1000个点
n = 800;
m = 1200;
t = 0:1/fs:(n-1)/fs;
tt= 0:1/fs:(m-1)/fs;
x = 0.4*sin(2*pi*t*f1) + 0.2*sin(2*pi*t*f2) + 0.1*sin(2*pi*t*f3);
% 补零到1200
x1 = [x zeros(1,1200-length(x))];
% 插值到1200
t2 = 0:1/fs/1.5:(n-1)/fs;
% 进行插值
x2 = interp1(t,x,t2,'linear');
x3 = 0.4*sin(2*pi*tt*f1) + 0.2*sin(2*pi*tt*f2) + 0.1*sin(2*pi*tt*f3);
% 进行FFT变换
y  = fft(x);
y1 = fft(x,1200);
y2 = fft(x1);
y3 = fft(x2);
y4=fft(x3);
% 计算,横坐标换算为Hz，纵坐标换算为幅值
figure(1)
plot(fs*[0:length(x)-1]/length(x),abs(y)*2/length(x));title('采样点 800 ');
figure(2)
plot(fs*[0:length(x1)-1]/length(x1),abs(y1)*2/length(x1));title('“高密度”的FFT变换（即FFT变换的点数大于信号的点数）');
figure(3)
plot(fs*[0:length(x1)-1]/length(x1),abs(y2)*2/length(x));title('对原序列进行补零后再进行FFT变换');
figure(4)
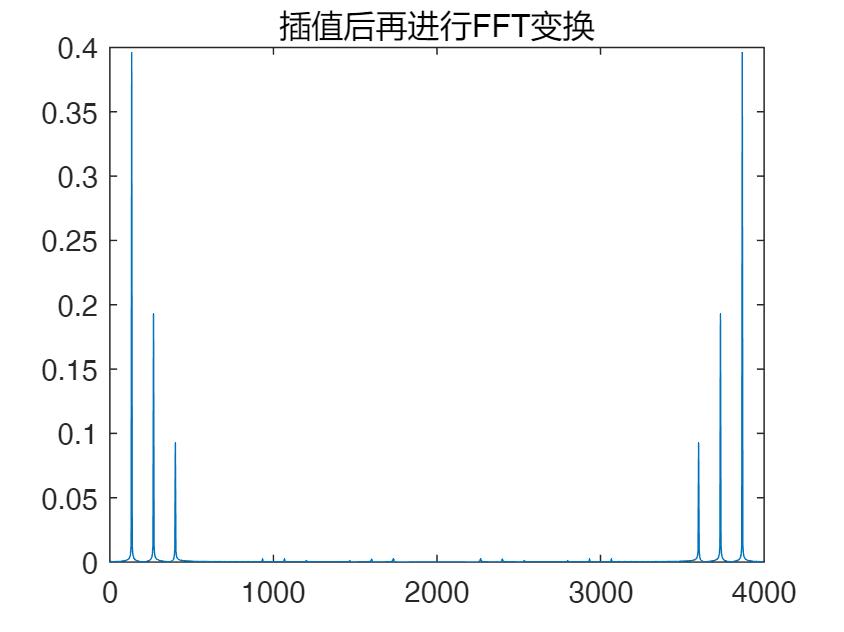
plot(fs*[0:length(x2)-1]/length(x2),abs(y3)*2/length(x2));title('插值后再进行FFT变换');
figure(5)
plot(fs*[0:length(x3)-1]/length(x3),abs(y4)*2/length(x3));title('对采样时间延长的信号序列进行FFT变换');

上面五个结果分辨是对原信号直接进行傅立叶变换，第二个是进行“高密度”的FFT变换（即FFT变换的点数大于信号的点数），第三个是对原序列进行补零后再进行FFT变换，第四个是进行插值后再进行FFT变换，第五个是对采样时间延长的信号序列进行FFT变换。

结果如图所示：

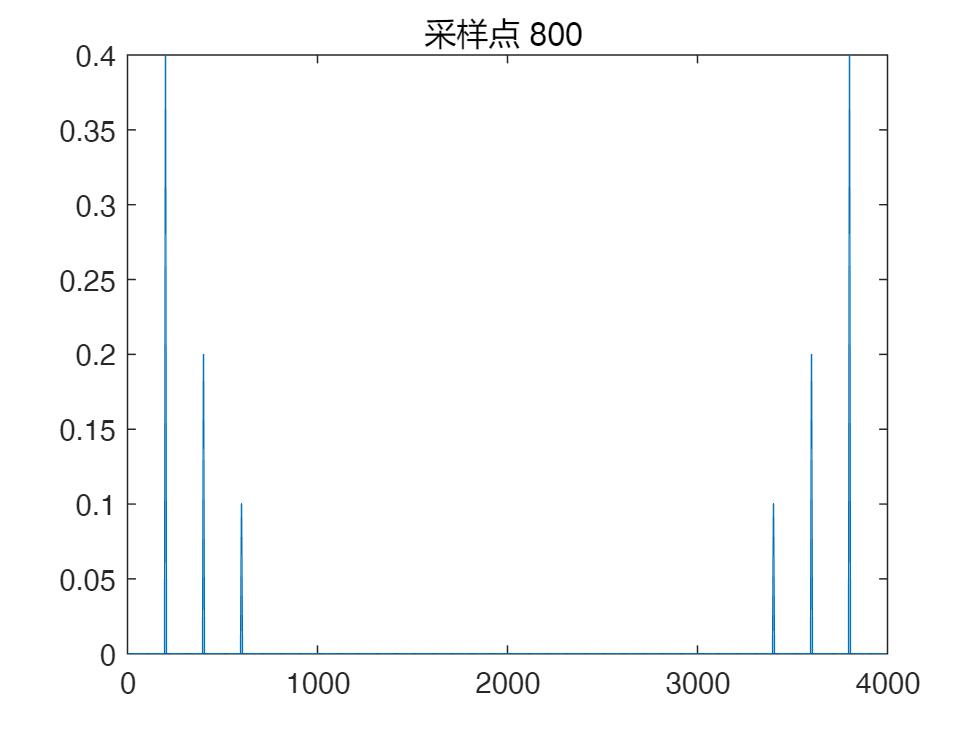
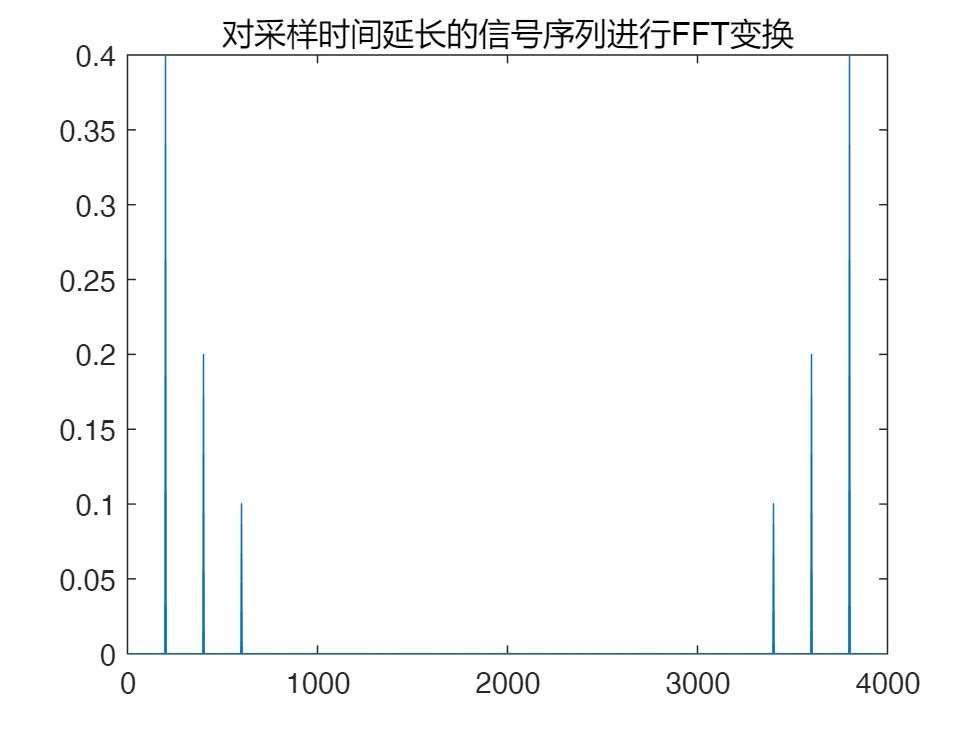
通过两幅图的结果我们可以发现，采样时间延长的谱线会更细一点，频谱的分辨率会更高（即能区分的频率间隔更小），这一点通过对两幅图放大后可以更加直观的发现。

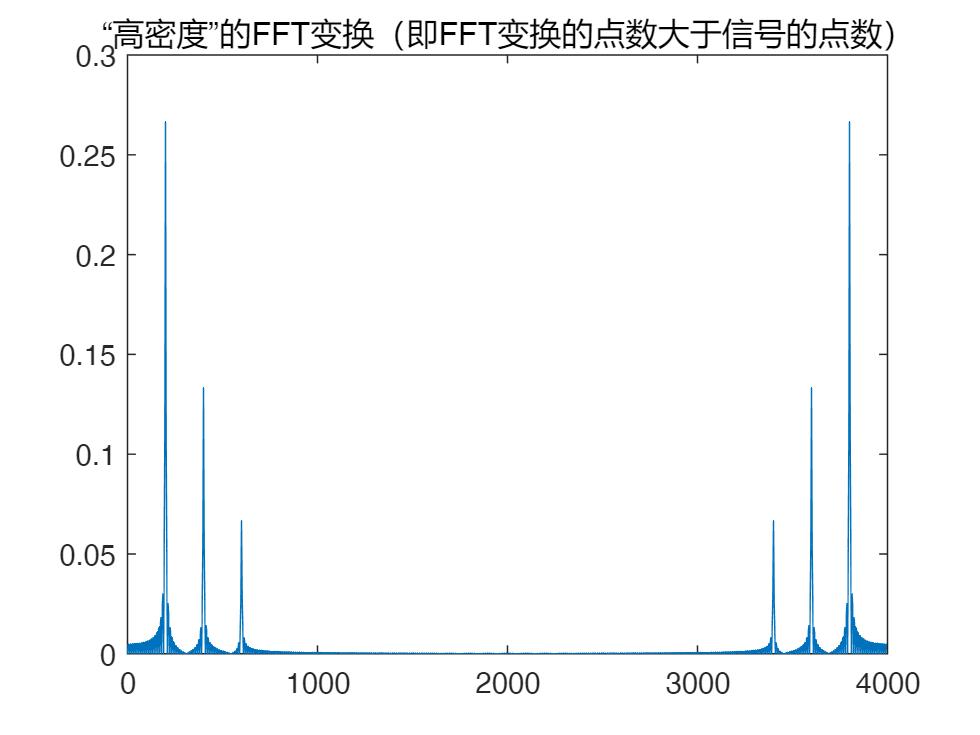
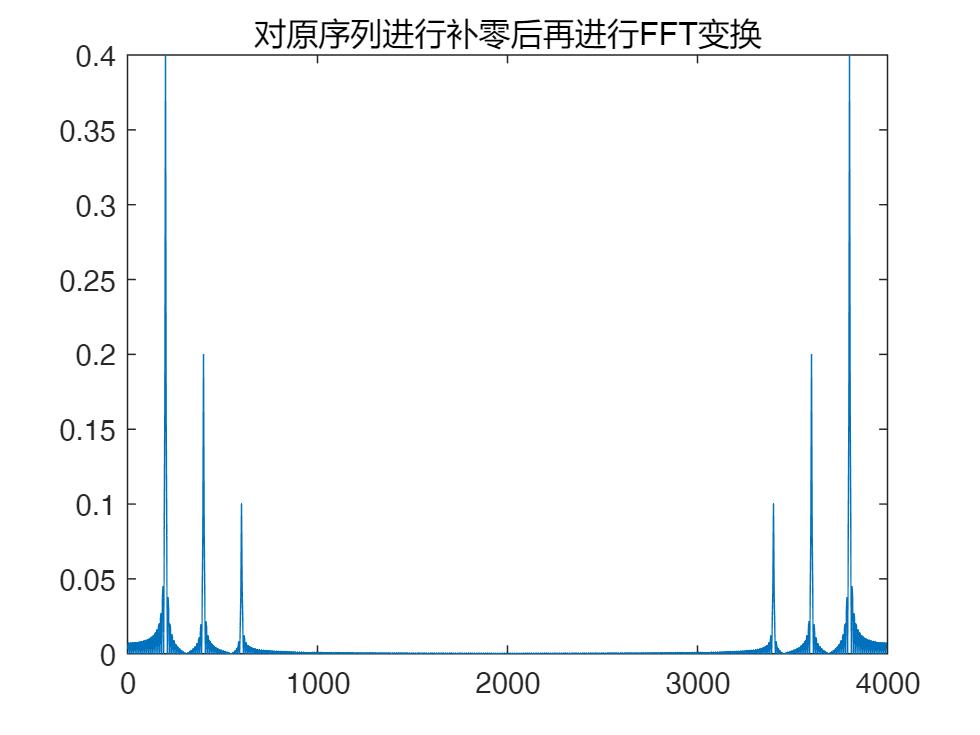
通过上面三幅图的结果可以发现：图一跟图二是一样的，这是因为高密度FFT的处理过程也是先对原序列补零然后再进行FFT，所以两种结果是一样的。

这也提示我们不用自己人为地去给序列做补零操作，在Matlab的变换中，只需要改变进行FFT变换的点数即可。

虽然插值后时域点数增多，但是插值后的谱线宽度也没有减小，这是因为插值相当于提高了采样频率，所以点数会增多，但是采样的时间并没有变，所以频率的分辨率并没有变小，即谱线并没有变细。

如果通过细致地观察，我们还可以发现原序列插值后的FFT结果的旁瓣会减小，但是会出现别的频率分量（小凸起）

频谱泄露

信号的截断

傅里叶变换是研究整个时间域和频率域的关系．然而，当运用计算机实现工程测试信号处理时，不可能对无限长的信号进行测量和运算，而是取其有限的时间片段进行分析。

做法是从信号中截取一个时间片段，然后用观察的信号时间片段进行周期延拓处理，得到虚拟的无限长的信号，然后就可以对信号进行傅里叶变换、相关分析等数学处理。

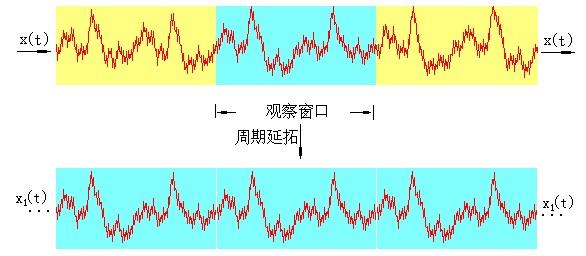
频谱泄露定义

周期延拓后的信号与真实信号是不同的，下面从数学的角度来看这种处理带来的误差情况。

设有余弦信号x（t）在时域分布为无限长（- ∞，∞），当用矩形窗函数w(t)与其相乘时，得到截断信号xT(t)=x(t)w(t)。根据博里叶变换关系，余弦信号的频谱X（ω）是位于ω。处的δ函数，而矩形窗函数w(t)的谱为sinc(ω)函数，按照频域卷积定理，则截断信号xT(t)的谱XT(ω) 应为

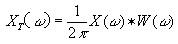
将截断信号的谱 XT(ω)与原始信号的谱X（ω）相比较可知，它已不是原来的两条谱线，而是两段振荡的连续谱．这表明 原来的信号被截断以后，其频谱发生了畸变，原来集中在f0处的能量被分散到两个较宽的频带中去了，这种现象称之为频谱能量泄漏（Leakage）。

信号截断以后产生的能量泄漏现象是必然的

因为窗函数w(t)是一个频带无限的函数，所以即使原信号x(t)是限带宽信号，而在截断以后也必然成为无限带宽的函数，即信号在频域的能量与分布被扩展了。

又从采样定理可知，无论采样频率多高，只要信号一经截断，就不可避免地引起混叠，因此信号截断必然导致一些误差，这是信号分析中不容忽视的问题。

窗

窗的概念

如果增大截断长度T，即矩形窗口加宽，则窗谱W（ω）将被压缩变窄（π／T减小）。虽然理论上讲，其频谱范围仍为无限宽，但实际上中心频率以外的频率分量衰减较快，因而泄漏误差将减小。

当窗口宽度T趋于无穷大时，则谱窗W（ω）将变为δ（ω）函数，而δ（ω）与X（ω）的卷积仍为H（ω），这说明，如果窗口无限宽，即不截断，就不存在泄漏误差。

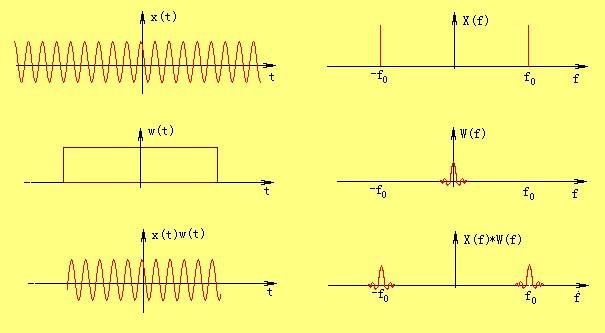
为了减少频谱能量泄漏，可采用不同的截取函数对信号进行截断，截断函数称为窗函数，简称为窗。泄漏与窗函数频谱的两侧旁瓣有关，如果两侧p旁瓣的高度趋于零，而使能量相对集中在主瓣，就可以较为接近于真实的频谱。

为此，在时间域中可采用不同的窗函数来截断信号。

以上是关于FFT频谱分析（补零频谱泄露栅栏效应加窗细化频谱混叠），MatlabC语言代码的主要内容，如果未能解决你的问题，请参考以下文章

虹科教您 | 实时频谱分析仪中如何选择合适的FFT窗函数

关于用FFT分析信号频谱的问题

Window Function--the function of window function

使用 FFT 进行频谱分析，基频推导

用MATLAB设计对信号进行频谱分析和滤波处理的程序

在 Java 中使用 FFT 算法进行音频频谱分析