行列式04---k 级子式与余子式代数余子式与拉普拉斯定理
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了行列式04---k 级子式与余子式代数余子式与拉普拉斯定理相关的知识,希望对你有一定的参考价值。
1 、 k 级子式与余子式、代数余子式
定 义 1 \\large\\color{magenta}{\\boxed{\\color{brown}{定义 1} }} 定义1 在一个 n n n 级行列式 D D D 中任意选定 k k k 行 k k k 列 ( k ≤ n ) , (k \\leq n), (k≤n), 位于这些行和列的交叉点上的 k 2 k^{2} k2 个元素按照原来次序组成一个 k k k 级行列式 M , M, M, 称为行列式 D D D 的一个 k k k 级 子 式 \\large\\color{#70f3ff}{\\boxed{\\color{green}{子式}}} 子式.
若行与列的选法一致,称 S S S 为 k k k 阶 主 子 式 \\large\\color{#70f3ff}{\\boxed{\\color{green}{主子式}}} 主子式 .
若选取前 k \\boldsymbol{k} k 行前 k \\boldsymbol{k} k 列,称 S \\boldsymbol{S} S 为 k \\boldsymbol{k} k 阶 顺 序 主 子 式 \\large\\color{#70f3ff}{\\boxed{\\color{green}{顺序主子式}}} 顺序主子式 .
在 D D D 中划去 M M M所在的 k k k 行 k k k 列后余下的元素按照原来的次序组成的 n n n - k k k 级行列式 M ′ M^{\\prime} M′ 称为 k k k 级子式 M \\mathrm{M} M 的 余 子 式 \\large\\color{#70f3ff}{\\boxed{\\color{green}{余子式}}} 余子式。
若 k k k 级子式 M M M 在 D \\mathrm{D} D 中所在的行、列指标分别是 i 1 , i 2 , ⋯ , i k ; j 1 , j 2 , ⋯ , j k \\boldsymbol{i}_{1}, \\boldsymbol{i}_{2}, \\cdots, \\boldsymbol{i}_{k} ; \\boldsymbol{j}_{1}, \\boldsymbol{j}_{2}, \\cdots, \\boldsymbol{j}_{k} i1,i2,⋯,ik;j1,j2,⋯,jk,则在 M M M 的余子式 M ′ M^{\\prime} M′ 前加上符号 ( − 1 ) i 1 + i 2 + ⋯ + i k + j 1 + j 2 + ⋯ + j k (-1)^{i_{1}+i_{2}+\\cdots+i_{k}+j_{1}+j_{2}+\\cdots+j_{k}} (−1)i1+i2+⋯+ik+j1+j2+⋯+jk 后,称之为 M \\mathrm{M} M 的 代 数 余 子 式 \\large\\color{#70f3ff}{\\boxed{\\color{green}{代数余子式}}} 代数余子式 , 记为 A = ( − 1 ) i 1 + i 2 + ⋯ + i k + j 1 + j 2 + ⋯ + j k M ′ A=(-1)^{i_{1}+i_{2}+\\cdots+i_{k}+j_{1}+j_{2}+\\cdots+j_{k}} M^{\\prime} A=(−1)i1+i2+⋯+ik+j1+j2+⋯+jkM′.
例 1 \\Large\\color{violet}{例 1} 例1
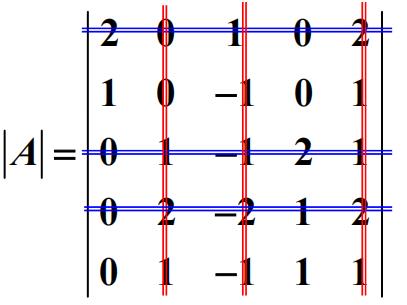
选取 1,3 行, 2,3 列相应的子式,
余
子
式
\\Large{\\color{blue}{余子式}}
余子式 ,
代
数
余
子
式
\\Large{\\color{red}{代数余子式}}
代数余子式:
S
1
=
∣
0
1
1
−
1
∣
M
1
=
∣
1
0
1
0
1
2
0
1
1
∣
A
1
=
(
−
1
)
1
+
3
+
2
+
3
M
1
=
−
M
1
S_{1}=\\left|\\begin{array}{cc} 0 & 1 \\\\ 1 & -1 \\end{array}\\right| \\quad{\\color{blue}{M_{1}}} =\\left|\\begin{array}{lll} 1 & 0 & 1 \\\\ 0 & 1 & 2 \\\\ 0 & 1 & 1 \\end{array}\\right| \\quad {\\color{red}{A_{1}}} =(-1)^{1+3+2+3} M_{1}=-M_{1}
S1=∣∣∣∣011−1∣∣∣∣M1=∣∣∣∣∣∣100011121∣∣∣∣∣∣A1=(−1)1+3+2+3M1=−M1以上是关于行列式04---k 级子式与余子式代数余子式与拉普拉斯定理的主要内容,如果未能解决你的问题,请参考以下文章