吴恩达机器学习-6-机器学习的建议
Posted 尤尔小屋的猫
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了吴恩达机器学习-6-机器学习的建议相关的知识,希望对你有一定的参考价值。
出品:尤而小屋
作者:Peter
编辑:Peter
吴恩达机器学习-6-机器学习的建议
本文中记录的是吴恩达老师对机器学习的建议,包含:
- 应用机器学习的建议
- 评估假设
- 模型选择和交叉验证
- 方差和偏差诊断
- 正则化与过拟合问题
应用机器学习的建议
当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差,我们下一步可以做什么?
- 获得更多的训练样本
- 尝试减少特征的数量
- 尝试获得更多的特征
- 尝试增加多项式特征
- 尝试减少正则化程度 λ \\lambda λ
- 尝试增加正则化程度 λ \\lambda λ
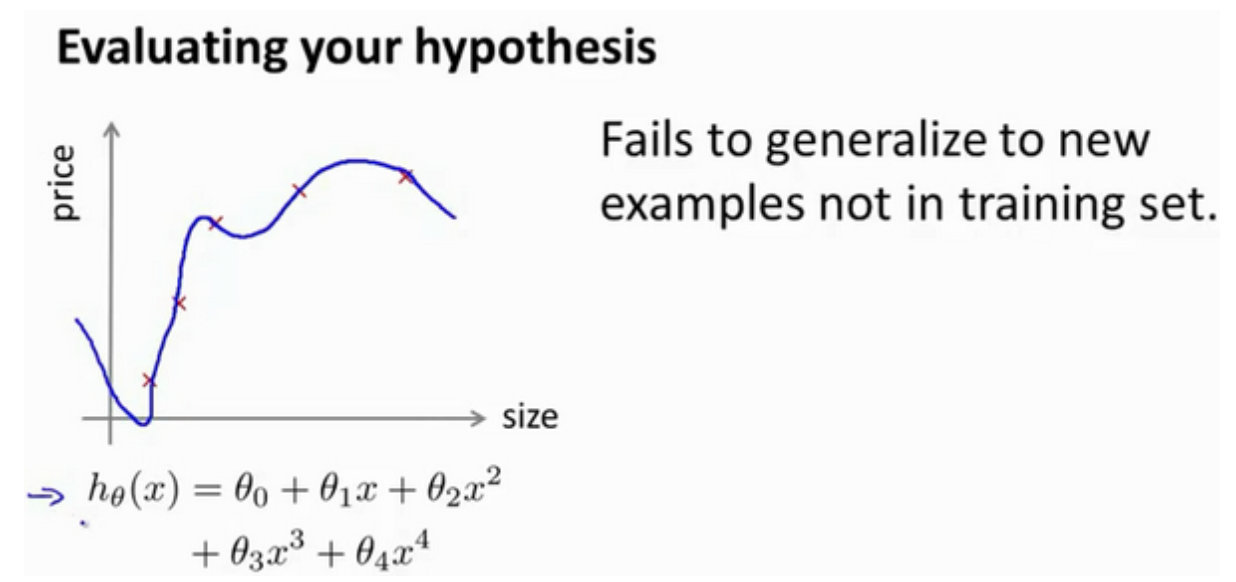
评估假设Evaluating a Hypothesis
当学习的算法时候,考虑的是如何选择参数来使得训练误差最小化。在模型建立的过程中很容易遇到过拟合的问题,那么如何评估模型是否过拟合呢?
为了检验算法是否过拟合,将数据集分成训练集和测试集,通常是7:3的比例。关键点是训练集和测试集均要含有各种类型的数据,通常我们要对数据进行“洗牌”,然后再分成训练集和测试集。

当我们在训练集上得到我们的学习模型之后,就需要使用测试集合来检验该模型,有两种不同的方法:
- 线性回归模型:利用测试数据计算代价函数 J J J
- 逻辑回归模型:
- 先利用测试数据计算代价函数$J_{test}{(\\theta)} $
- 在针对每个测试集样本计算误分类的比率,再求平均值
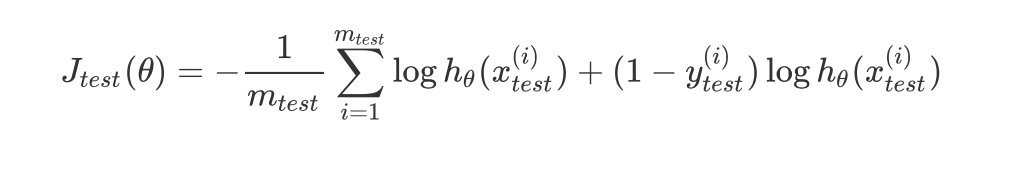
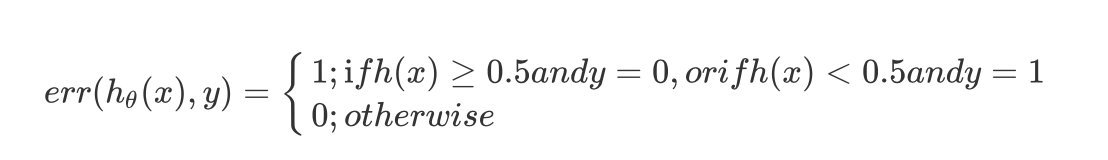
模型选择和交叉验证
交叉验证
什么是交叉验证?
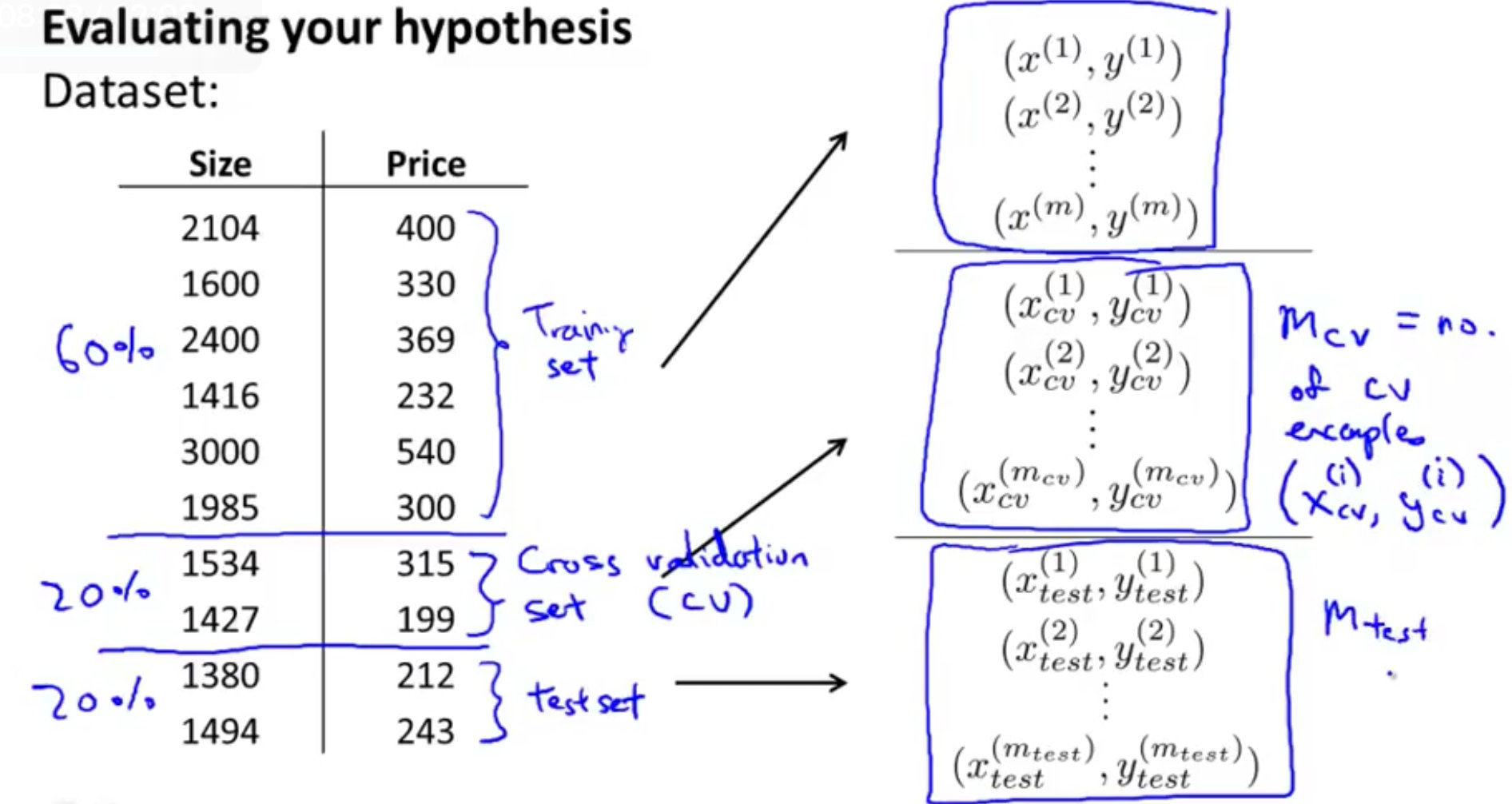
交叉验证集合指的是:使用60%的数据作为*训练集,使用 20%*的数据作为*交叉验证集,使用20%*的数据作为测试集
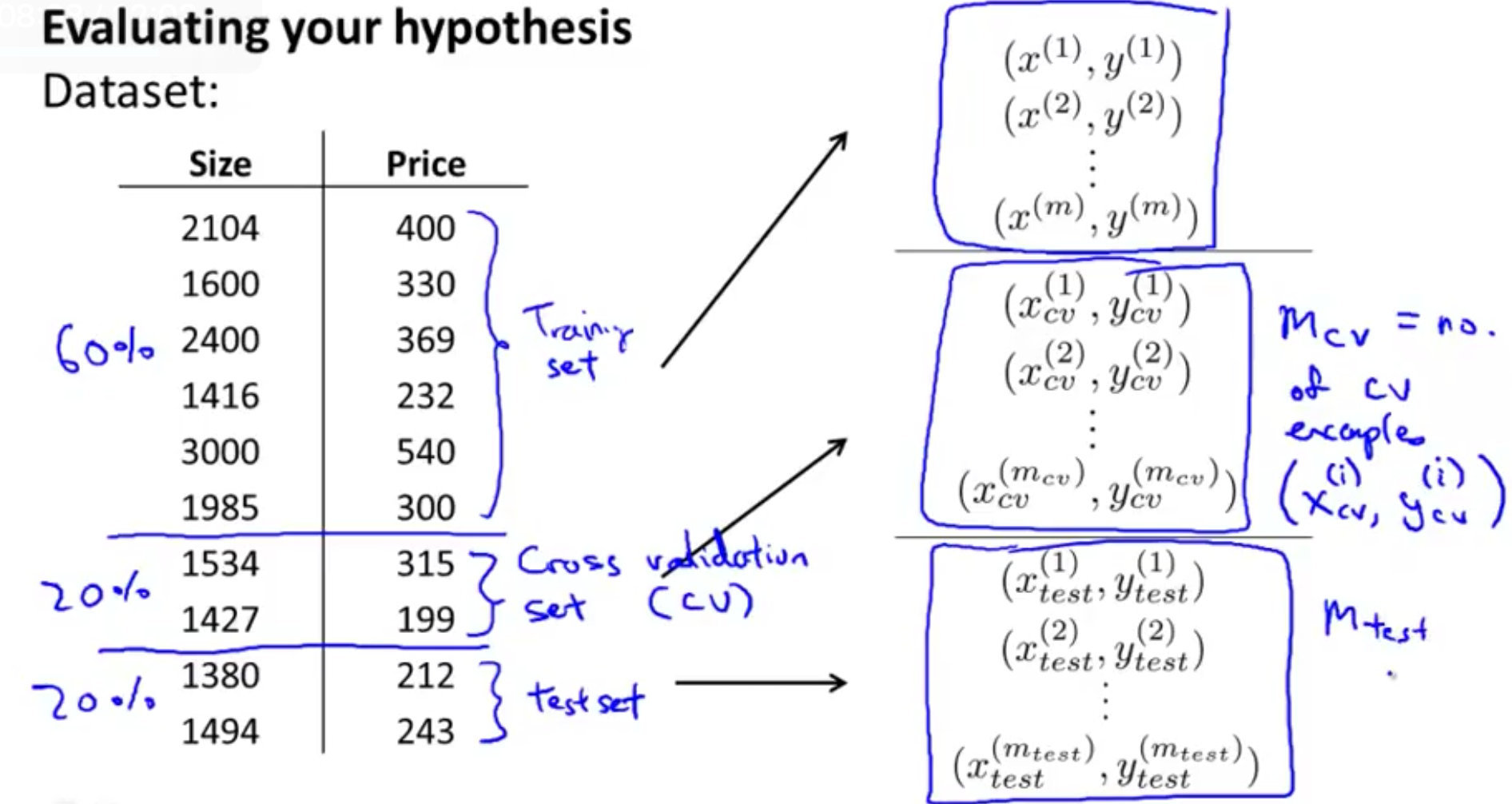
模型选择
- 使用训练集训练出10个模型
- 用10个模型分别对交叉验证集计算得出交(代价函数的值)
- 选取代价函数值最小的模型
- 用上面步骤中选出的模型,对测试集计算得出推广误差(代价函数的值)
- 训练误差表示为:
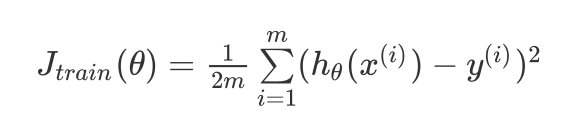
KaTeX parse error: Expected group after '_' at position 38: …frac{1}{2m}\\sum_̲\\limits{i=1}^{m…
- 交叉验证误差(通过交叉验证数据集得到的)表示为:
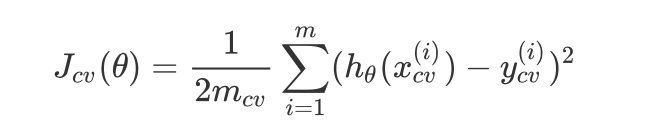
- 测试误差

诊断方差和偏差Diagnosing Bias vs. Variance
如果一个算法的运行结果不是很理想,只有两种情况:要么偏差过大,要么方差过大。换句话就是说,要么出现欠拟合,要么出现过拟合。

通过训练集和交叉验证集的代价函数误差和多项式的次数绘制在同张图中:

1. 高偏差阶段
交叉验证集和训练集的代价函数误差都是很大,近似相等;
2. 高方差阶段
交叉验证集的误差远大于训练集的误差,训练集的误差很低
正则化和偏差/方差Regularization and Bias_Variance
正则化基础
正则化技术主要是为了解决过拟合的问题。过拟合指的是:对样本数据具有很好的判断能力,但是对新的数据预测能力很差。
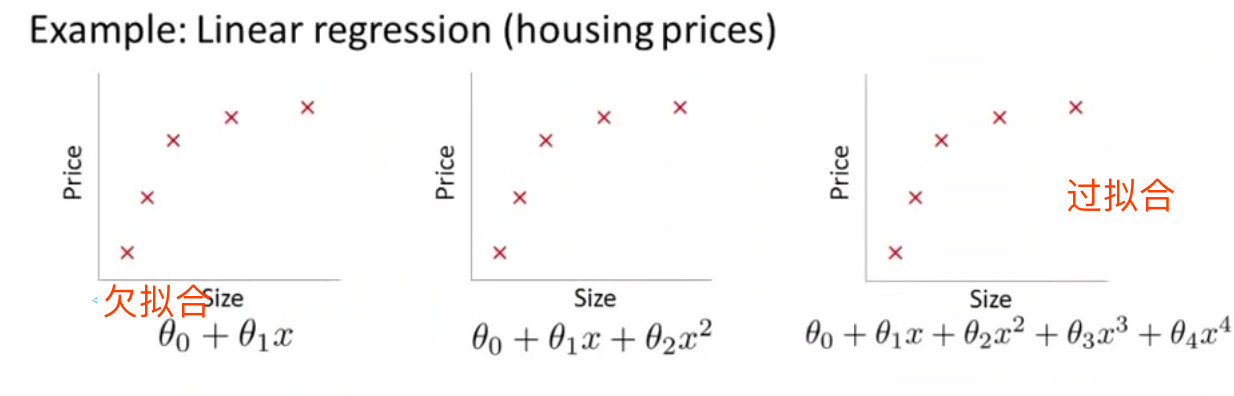
- 第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集
- 第三个模型是一个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据
- 中间的模型似乎最合适
栗子
假设我们需要对下图中的多项式进行拟合,需要正则化项

- 当 λ \\lambda λ很大的时候,出现高偏差,假设 h θ ( x ) h_\\theta(x) hθ(x)是一条直线
- 当 λ \\lambda λ很小约为0的时候,出现高方差


如果是多项式拟合,x的次数越高,拟合的效果越好,但是相应的预测能力就可能变差。对于过拟合的处理:
- 丢弃一些不能正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法,例如PCA
- 正则化。 保留所有的特征,但是减少参数的大小(magnitude)

加入正则化参数
在模型 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 h_\\theta(x)=\\theta_0+\\theta_1x_1+\\theta_2x_2+\\theta_3x_3+\\theta_4x_4 hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4中,主要是高次项产生的过拟合问题:

加入正则化参数后能够防止过拟合问题,其中 λ \\lambda λ是正则化参数Regularization Parameter :
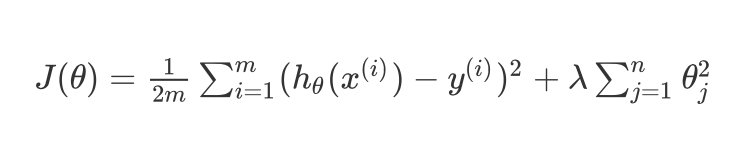
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J(\\theta)=\\frac{1}{2m}\\sum^m_{i=1}(h_{\\theta}(x^{(i)})-y^{(i)})^2+\\lambda \\sum^n_{j=1}\\theta^2_{j} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2
Attention:一般地,不对 θ 0 \\theta_0 θ0进行惩罚;加上正则化参数实际上是对参数 θ \\theta θ进行惩罚。经过正则化处理后的模型和原模型的对比:
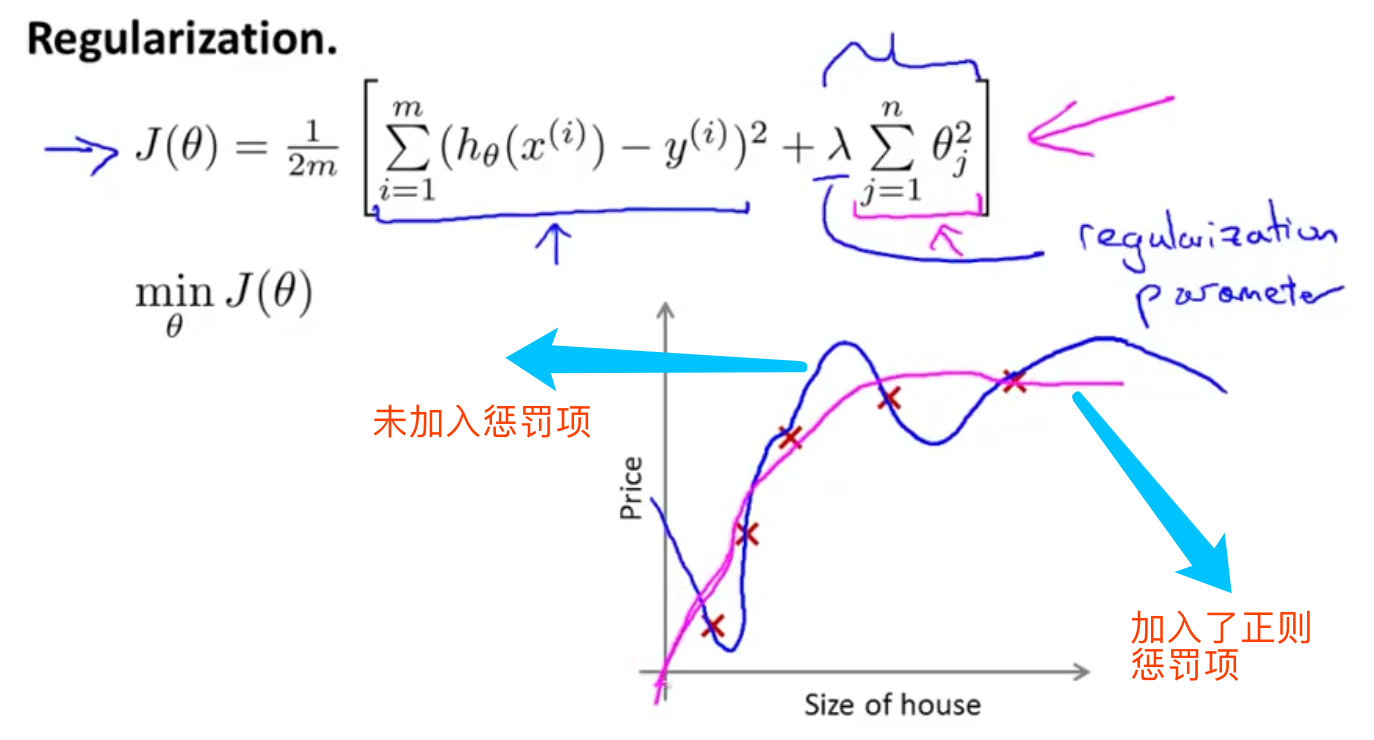
- 如果 λ \\lambda λ过大,所有的参数最小化,模型变成了 h θ ( x ) = θ 0 h_\\theta(x)=\\theta_0 hθ(x)=θ0,造成了过拟合
参数 λ \\lambda λ的选择
- 使用训练集训练出多个不同程度的正则化模型
- 用多个模型分别对交叉验证集计算的出交叉验证误差
- 选择得出交叉验证误差最小的模型
- 运用步骤3中选出模型对测试集计算得出推广误差
学习曲线 Learning Curves
使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。
学习曲线是将训练集误差和交叉验证集误差作为训练集样本数量 m m m的函数绘制的图表
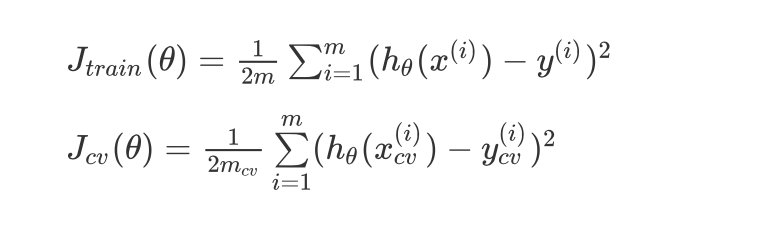
J t r a i n ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J_{train}(\\theta) = \\frac{1}{2m}\\sum_{i=1}^{m}(h_{\\theta}(x^{(i)})-y^{(i)})^2 Jtrain(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
KaTeX parse error: Expected group after '_' at position 42: …1}{2m_{cv}}\\sum_̲\\limits{i=1}^{m…
训练样本m和代价函数J的关系
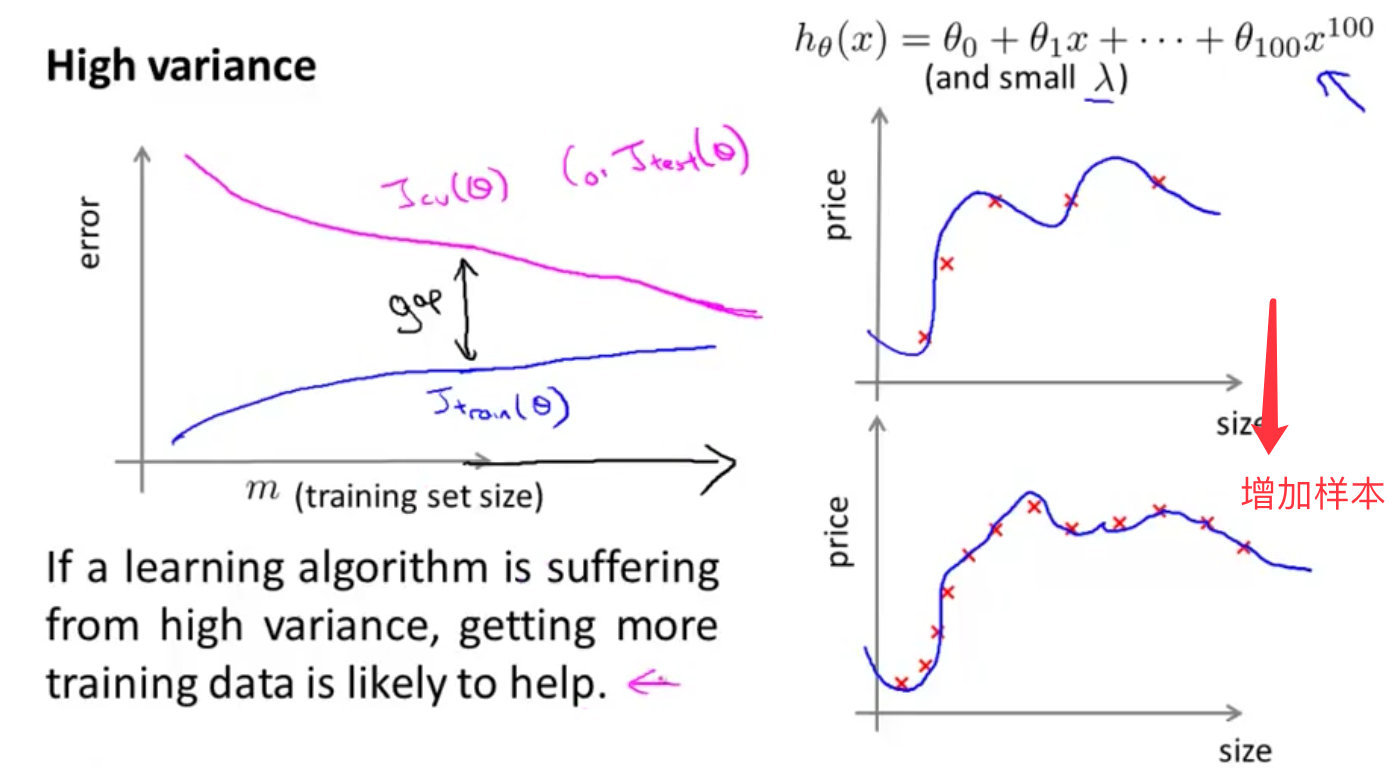
从下图1中看出结果
- 样本越少,训练集误差很小,交叉验证集误差很大
- 当样本逐渐增加的时候,二者的差别逐渐减小
说明:在高偏差、欠拟合的情况下,增加样本数量没效果

在高方差的情况下,增加数量可以提高算法效果
总结
- 获得更多的训练样本——解决高方差
- 尝试减少特征的数量——解决高方差
- 尝试获得更多的特征——解决高偏差
- 尝试增加多项式特征——解决高偏差
- 尝试减少正则化程度λ——解决高偏差
- 尝试增加正则化程度λ——解决高方差
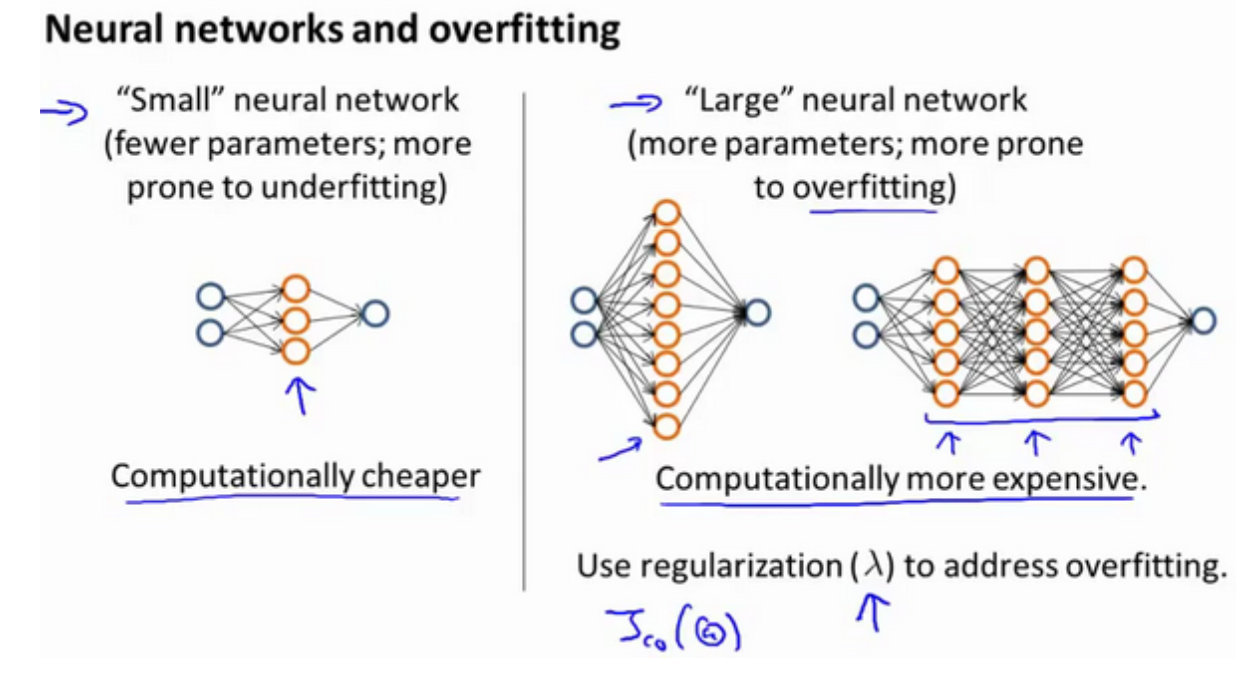
神经网络的方差和偏差
较小的神经网络,参数少,容易出现高偏差和欠拟合;
较大的神经网络,参数多,容易出现高方差和过拟合
通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好
查准率和查全率
| 预测值 | |||
|---|---|---|---|
| Positive | Negtive | ||
| 实际值 | True | TP | FN |
| False | FP | TN |
查准率precision:实际和预测同时为正例 / 预测值全部为正例
P
=
T
P
T
P
+
F
P
P=\\frac{TP}{TP+FP}
P=TP+FPTP 查全率recall:实际和预测同时为正例 / 实际值全部为正例
R
=
T
P
T
P
+
F
N
R = \\frac{TP}{TP+FN}
R=TP+FNTP
查全率和查准率是一对矛盾的量,一个高的话,另一个必定低,关系图如下:
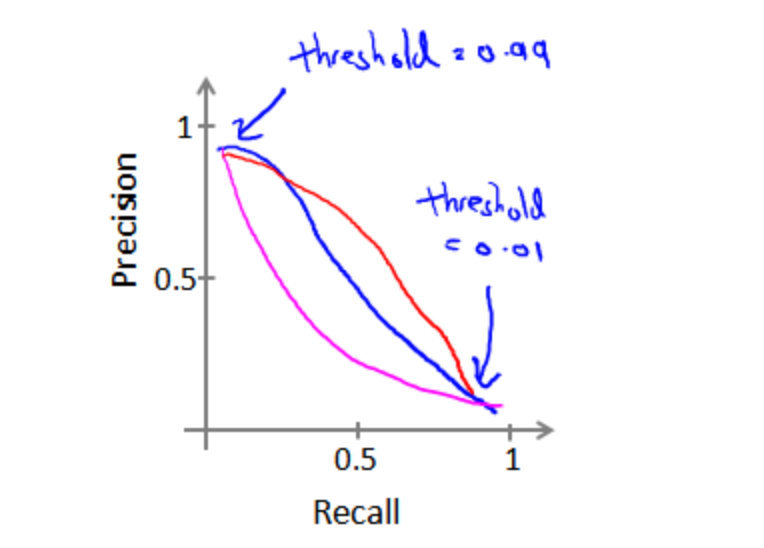
查全率和查准率之间的平衡点,一般是使用 F 1 F_1 F1系数表示 F 1 = 2 P R P + R F_1=\\frac{2PR}{P+R} F1=P+R2PR
以上是关于吴恩达机器学习-6-机器学习的建议的主要内容,如果未能解决你的问题,请参考以下文章
机器学习- 吴恩达Andrew Ng Coursera学习总结合集,编程作业技巧合集