吴恩达机器学习笔记-第六周

Posted 2020-10-31 jiangxinyang

十、应用机器学习的建议

10.1 决定下一步做什么

很多时候我们会发现我们通过最小化代价函数获得的模型所预测的值和真实值有很大的偏差(其实就是泛化能力差)，此时我们可以在训练完之后对我们的模型进行诊断测试。测试模型的有效性

10.2 评估一个hypothe假设

一个好的hypothesis是即要代价函数的值很小，又要具有很好的泛化能力，在这里我们通过加入测试集来测试我们的hypothesis是否具有较好的泛化能力。最简单的方法就是将我们的数据集D进行划分，一般70%划分到训练集，30%划分到测试集。

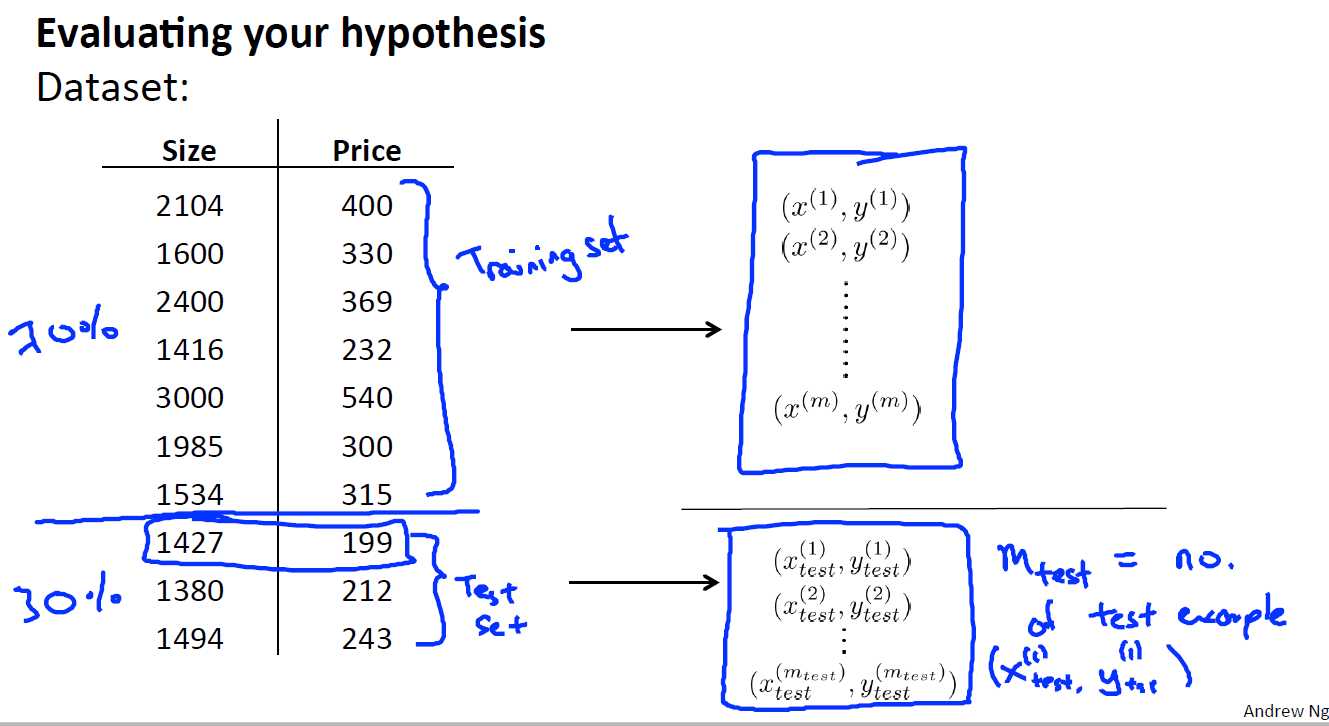
10.3 模型选择和交叉验证集

假如我们要在10个不同次数的二项式的模型中选择我们的模型，又或者是你想要选择合适的正规化参数，那么你该怎样去做这个选择？

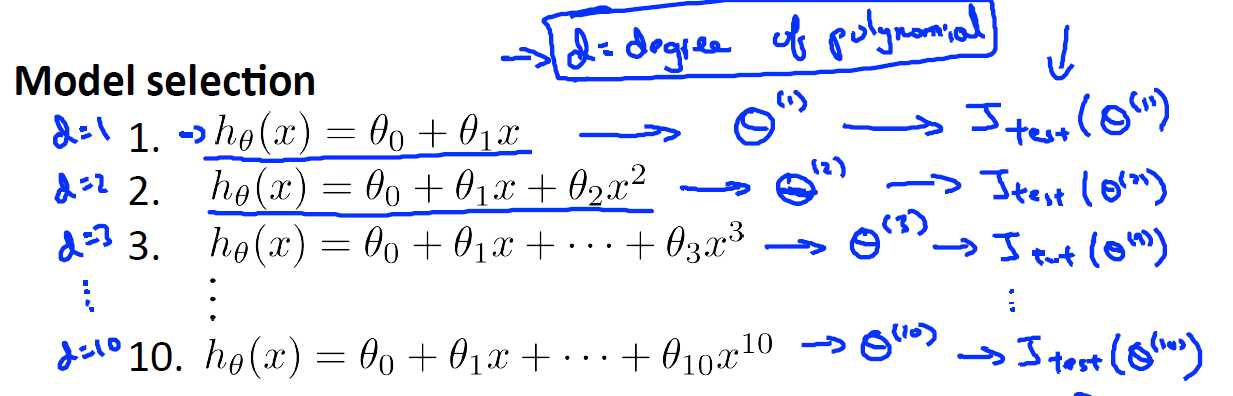
从经验上来说显然越高阶的多项式越来很好的描述我们的训练集，但是能不能很好的泛化那就不一定了，因此我们需要选择一个能满足两者的模型，此时我们就需要使用交叉验证集来帮助我们选取模型

在这里我们依然对数据集D进行拆分，60%的数据作为训练集，20%的数据作为交叉验证集，20%的数据作为测试集。

模型选择的方法：

1. 使用训练集训练出10个不同的模型

2. 使用交叉验证集进行验证，选择出交叉验证误差最小的模型

3. 对步骤2中选取出来的模型用测试集进行测试，得到测试误差(也称为推广误差)

10.4 诊断偏差和方差

偏差(Bias)的概念：偏差描述预测值的期望(期望就是平均值)和真实值的差距。

方差(Variance)的概念：方差描述的是离散程度，即预测值和预测值的期望之间的差距

两者的表现如下图所示

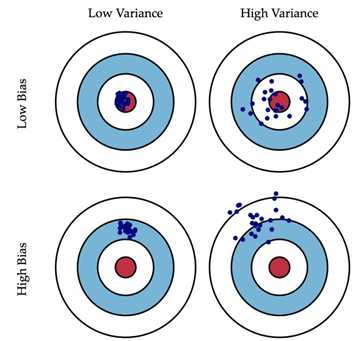
了解了偏差和方差的概念，我们可以将偏差、方差和欠拟合、过拟合联系起来，那么他们之间到底有什么样的关系呢？

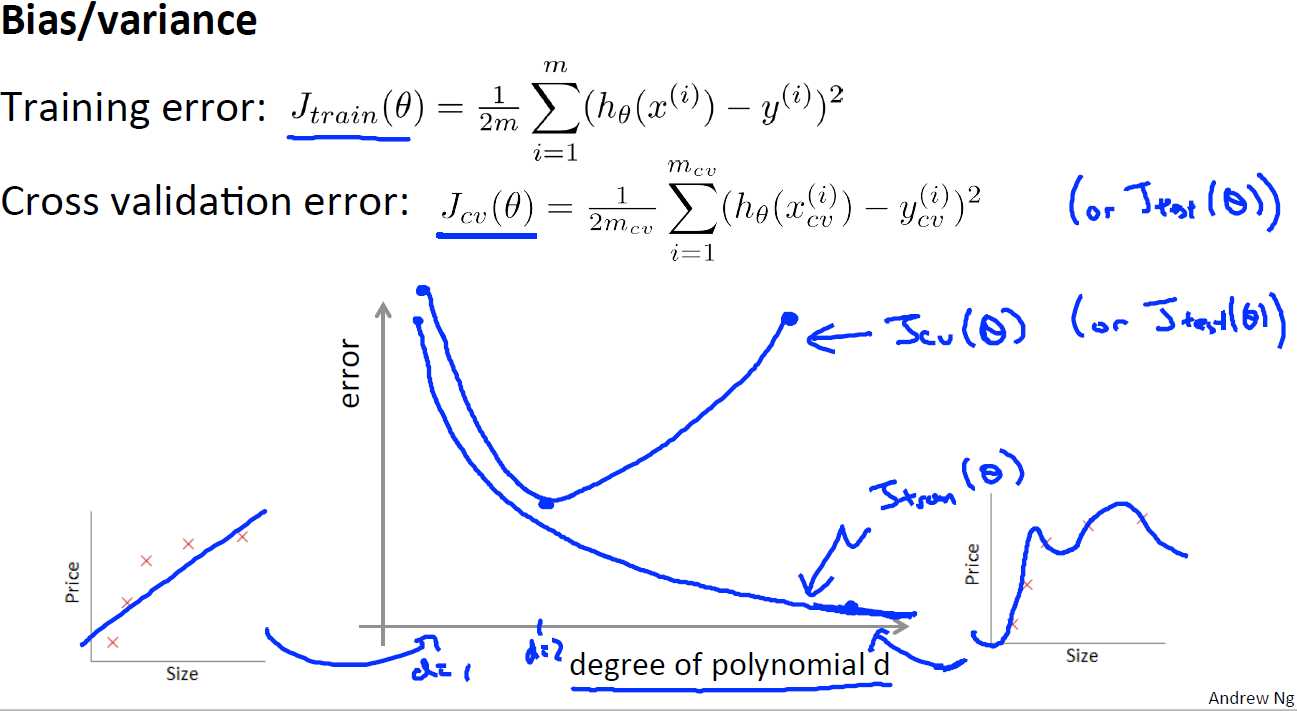
首先我们来看下交叉验证误差和训练误差的关系，可以看到当d(d表示多项式的最高阶的次数)较小时，交叉验证误差和训练误差都很大，此时其实是欠拟合的，而当d很大时，训练误差很小，交叉验证误差很大，此时是过拟合的，再结合偏差和方差的概念，可以得到：

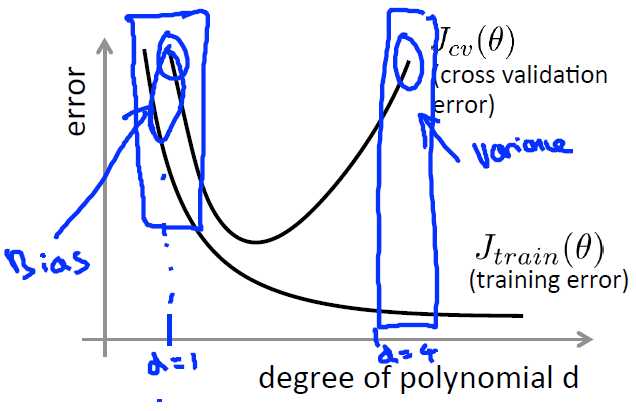
训练误差和交叉验证误差很接近，但又很大时：欠拟合/偏差大

训练误差和交叉验证误差相差很远时：过拟合/方差大

10.5 正则化和偏差/方差

前面说过为了避免过拟合我们会使用正则化，但是我们也说得正则化参数λ的选择很关键，λ太大，最后的hθ(x) = θ0，λ太小时，该正则项又不起作用，在选取合适的λ，我们在这里处理的方式和上面一样，采用交叉验证的方法

通常λ的取值是在0-10之间呈现两倍关系的值（如0,0.01,0.02,0.04,0.08，0.16，一直到10停止）然后把这些值依次加入到我们之前的模型中，然后采用交叉验证的方法去选取最合适的模型

再来看看偏差、方差和λ值的关系：

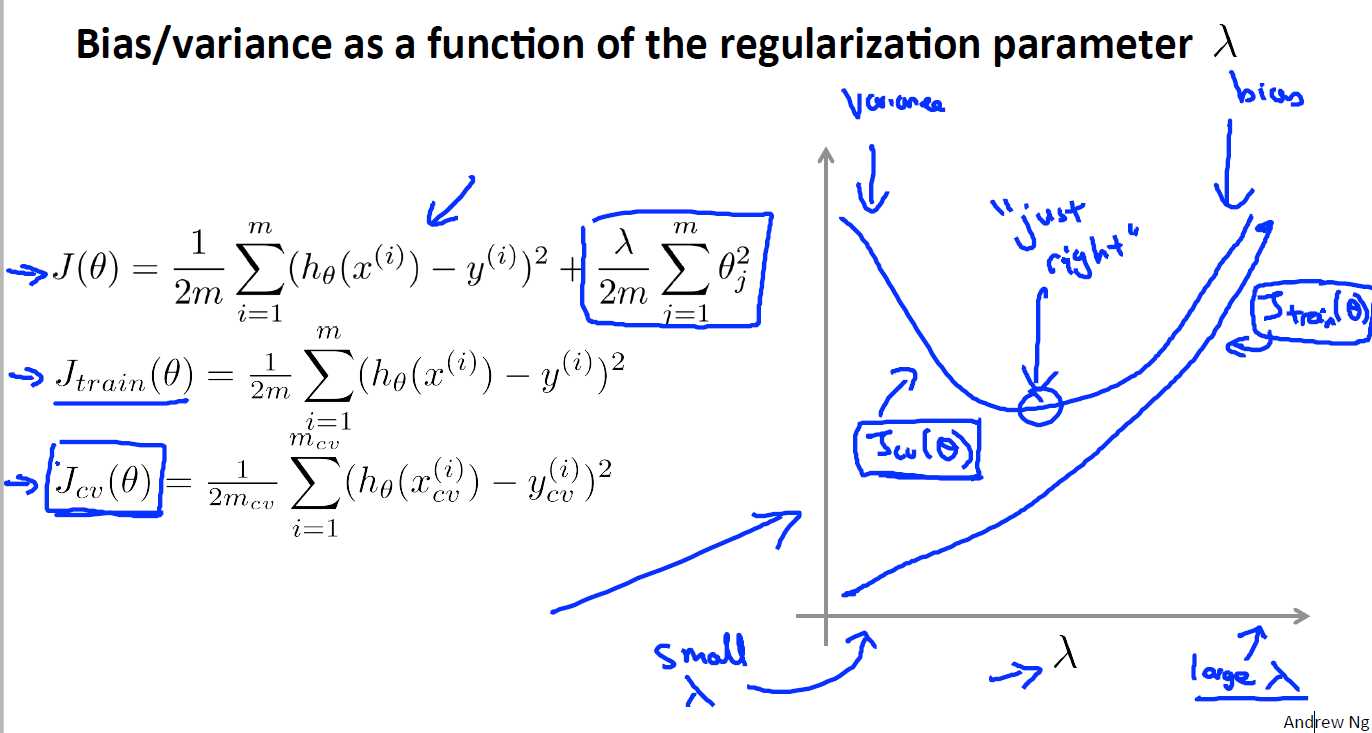
10.6 学习曲线

我们来看训练的数据集的大小对我们的模型有什么影响

在数据集很小的时候，我们很容易找到一个模型来很好的拟合它，此时的训练误差会很小，但是其泛化能力会很差，当数据集很多的时候，其测试误差会增大，但是其交叉验证误差会减小并且接近与测试误差，因此增加数据集的数量可以很好的处理过拟合的问题

但是对于欠拟合的问题呢？增加数据集是否有用：

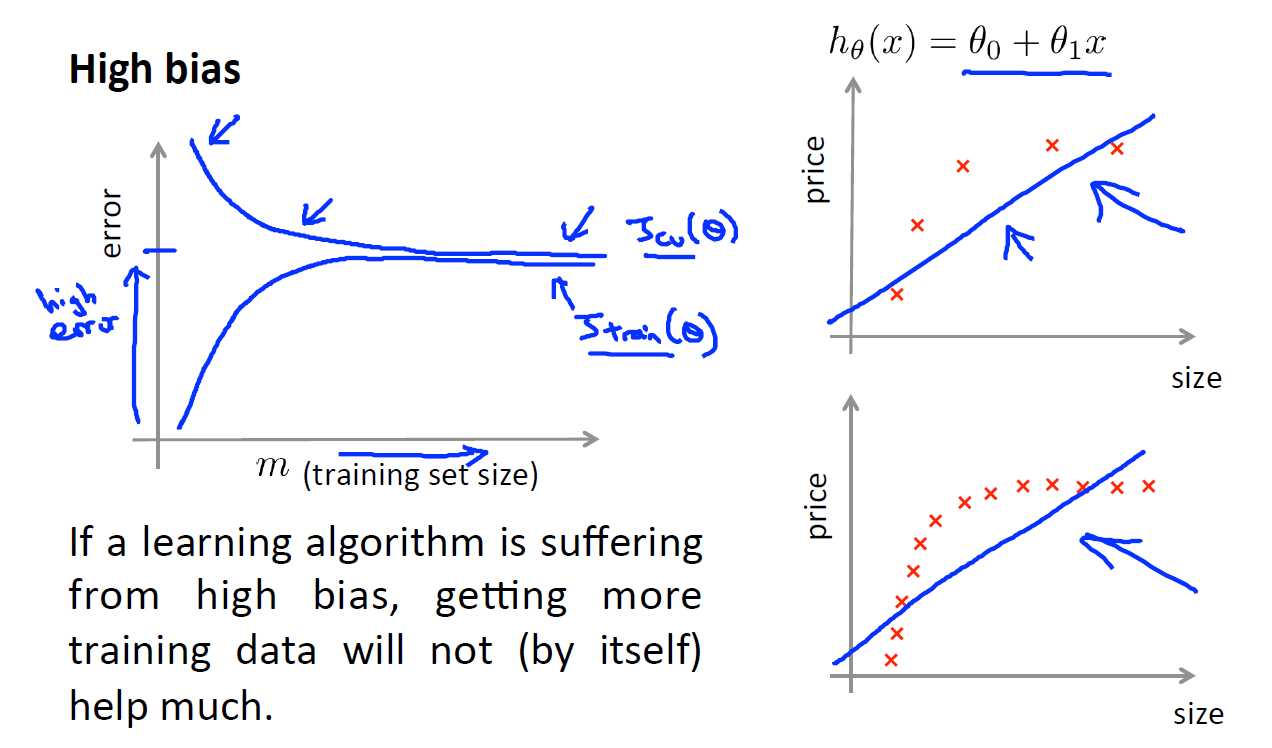
从上图可以看出，增大数据集虽然会使得测试误差和交叉验证误差很接近，但是两者都很大，偏离真实值，具有较大的偏差。

综上所述：对于欠拟合问题只能增加模型的复杂性来解决，即增加模型的维度，采用更高阶的多项式来描述；对于过拟合问题，可以通过增大数据集的形式来解决，但事实上数据集的数量要约等于10倍的特征维度才能避免过拟合，但现实中的数据特征维度会很大，而你的数据集又不会太多，因此最好的方法就是正则化降低维度。

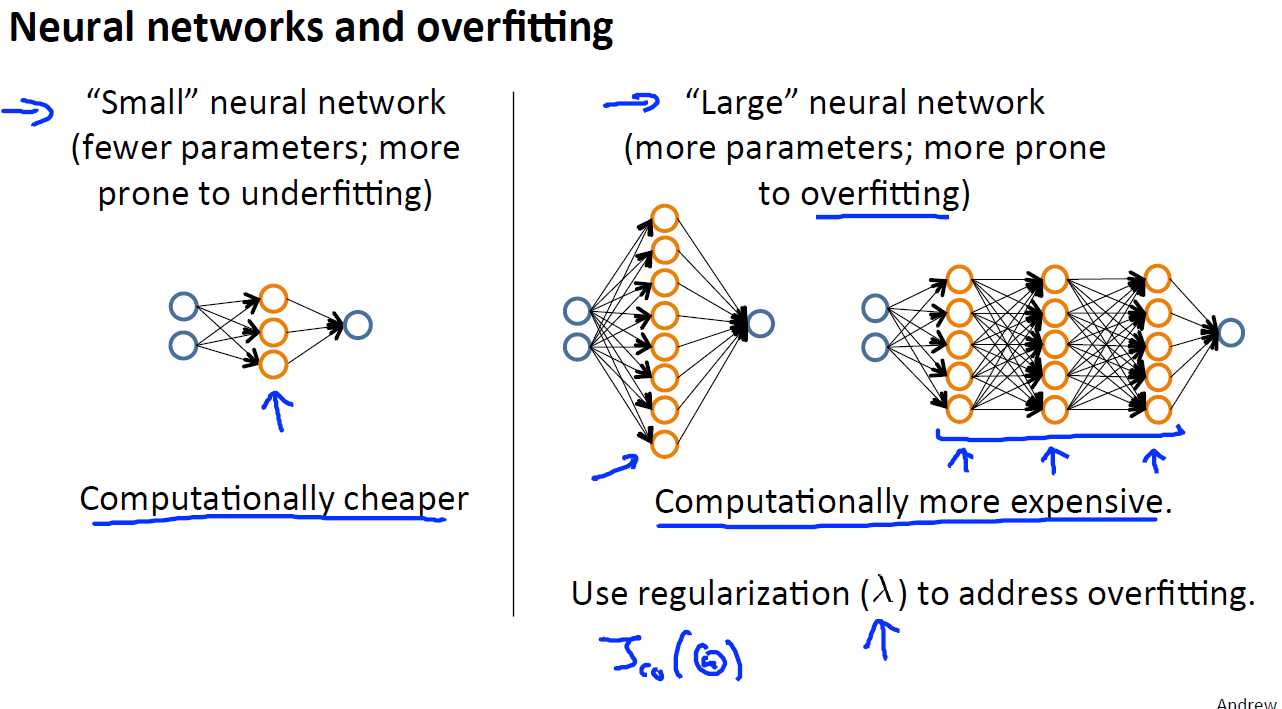
对于之前说到的神经网络，也会存在欠拟合和过拟合问题，一般来说，较小的神经网络容易出现欠拟合，较大的神经网络（较大的神经网络是要么隐藏层中的激活单元很多，要么隐藏层很多）会出现过拟合，通常来说采用较大的神经网络加上正则化处理所得到的结果要好于较小的神经网络，但相应的计算量也会大大的增加。而对于隐藏层数的选举，一般都是从一层开始选，然后逐渐的加层以获得更好的结果。

十一、机器学习系统的设计

11.1 首先要做什么

略

11.2 误差分析

在很多时候你并不知道你需要哪些复杂的特征变量，或者是否需要更多的数据。因此在一开始尽量先快速的做一个简单的算法出来，再对其采用交叉验证的方法来检验数据，并将其学习曲线画出来，看看是否存在偏差或者方差的问题，如果存在再采用相应的办法去解决。

11.3 类偏斜的误差度量

类偏斜问题表现为训练集中一类的数据非常多，而另一类的数据非常少，比如在预测恶性肿瘤和良性肿瘤时，恶性肿瘤的实例只有0.5%，而良性肿瘤的实例99.5%，然而我们通过训练而得到的误差却有1%，也就是说我们在预测时，预测所有的都是良性肿瘤也是正确的，因为即使是这样，误差也只有0.5%，然而这样算法就没有任何意义了，因此针对这类的问题我们引入查准率和查全率

 我们在比较预测值和实际值时可以分为两大类：预测值与真实值相同，预测值与真实值相反。又可以分为四小类：

1. 正确肯定(True Posttive TP)：预测值和实际值都为真

2. 正确否定(True Negative TN)：预测值和实际值都为假

3. 错误肯定(False Positive FP)：预测值为真，实际值为假

4. 错误否定(False Negative FN)：预测值为假，实际值为真

综上可以总结下，前面两个字表示预测值和实际值是否一直，后面两个字表示预测值是为真还是为假

现在我们引入两个概念：查准率和查全率

查准率：TP/(TP+FP)表示的含义就是在你预测的真值中实际上为真的比例，也就是说你预测为真的正确概率有多大。比如在你预测有恶性肿瘤的病人中事实上有多少人是有恶性肿瘤的，因此查准率越高越好，代表着预测的准确性。

查全率：TP/(TP+FN)表示的含义就是你预测到的概率有多大，你预测为真（该真实际值也是真）占总的实际真值的概率。比如在实际上所有的患恶性肿瘤的病人中，你成功的预测出了多少位，因此查全率也是越高越好。而对于上面的肿瘤问题，恶性肿瘤的查全率为0，显然是不正确的。

综上来说，查准率注重准确性，就是你预测的时候错误值要少；查全率是注重全面性，比如上面的肿瘤问题，你需要准确的把患恶性肿瘤病人都给预测出来，而不是说只能预测出一半，另一半就不管了

11.4 查准率和查全率之间的权衡

我们在做逻辑回归时，一般采用0.5来作为阀值，但在类偏斜问题上可以该阀值不一定适用。

我们可以看看查准率和查全率的关系曲线

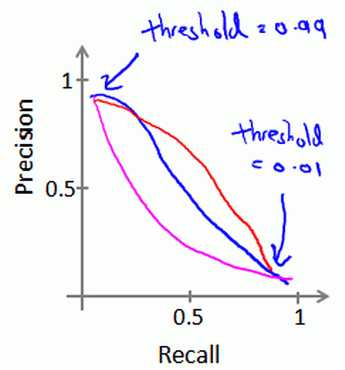
增大阀值可以提高查准率，降低阀值可以提高查全率，因此我们需要选择一个合适的阀值来确保我们具有较好的查准率和查全率

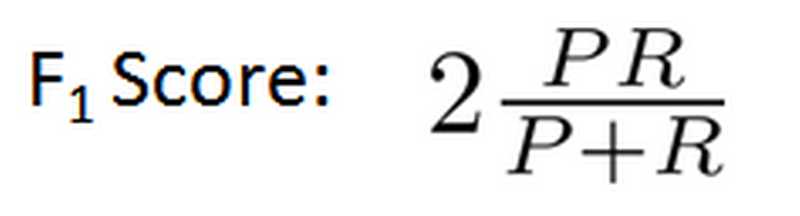
在这里P代表查准率，R代表查全率，我们选择使得F1值最高的阀值

11.5 机器学习的数据