车间调度基于改进蛙跳算法求解车间调度问题

Posted 2021-06-05 博主QQ2449341593

作业车间调度问题描述

作业车间调度问题（Job Shop Scheduling, JSP）是最经典的几个NP-hard问题之一。其应用领域极其广泛，涉及航母调度，机场飞机调度，港口码头货船调度，汽车加工流水线等。

JSP问题描述：一个加工系统有M台机器，要求加工N个作业，其中，作业i包含工序数为Li。令，则L为任务集的总工序数。其中，各工序的加工时间已确定，并且每个作业必须按照工序的先后顺序加工。调度的任务是安排所有作业的加工调度排序，约束条件被满足的同时，使性能指标得到优化。

作业车间调度需要考虑如下约束:

Cons1：每道工序在指定的机器上加工，且必须在其前一道工序加工完成后才能开始加工；

Cons2：某一时刻1台机器只能加工1个作业；

Cons3：每个作业只能在1台机器上加工1次；

Cons4：各作业的工序顺序和加工时间已知，不随加工排序的改变而改变。

问题实例

下面给出作业车间调度问题的一个实例，其中每个工序上标注有一对数值（m,p），其中，m表示当前工序必须在第m台机器上进行加工，p表示第m台机器加工当前工序所需要的加工时间。（注：机器和作业的编号从0开始）
jop0=[(0,3),(1,2),(2,2)]
jop1=[(0,2),(2,1),(1,4)]
jop2=[(1,4),(2,3)]
在这个例子中，作业jop0有3道工序：它的第1道工序上标注有(0,3)，其表示第1道工序必须在第0台机器上进行加工，且需要3个单位的加工时间；它的第2道工序上标注有(1,2)，其表示第2道工序必须在第1台机器上进行加工，且需要2个单位的加工时间；余下的同理。总的来说，这个实例中共有8道工序。
该问题的一个可行解是L=8道工序开始时间的一个排列，且满足问题的约束。下图给出了一个可行解（注：该解不是最优解）的示例：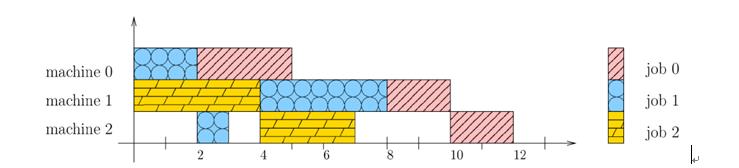

　蛙跳算法（SFLA）是一种全新的后启发式群体进化算法，具有高效的计算性能和优良的全局搜索能力。对混合蛙跳算法的基本原理进行了阐述，针对算法局部更新策略引起的更新操作前后个体空间位置变化较大，降低收敛速度这一问题，提出了一种基于阈值选择策略的改进蛙跳算法。通过不满足阈值条件的个体分量不予更新的策略，减小了个体空间差异，从而改善了算法的性能。数值实验证明了该改进算法的有效性，并对改进算法的阈值参数进行了率定

特点

　　SFLA由Eusuff和Lansey为解决组合优化问题于2003年最先提出。作为一种新型的仿生物学智能优化算法，SFLA 结合了基于模因（meme）进化的模因演算法（MA，memeticalgorithm）和基于群体行为的粒子群算法（PSO,particle swarm optimization）2 种群智能优化算法的优点。该算法具有概念简单，调整的参数少，计算速度快，全局搜索寻优能力强，易于实现的特点。混合蛙跳算法主要应用于解决多目标优化问题，例如水资源分配、桥墩维修、车间作业流程安排等工程实际应用问题。

原理

　　蛙跳算法的思想是：在一片湿地中生活着一群青蛙。湿地内离散的分布着许多石头，青蛙通过寻找不同的石头进行跳跃去找到食物较多的地方。每只青蛙个体之间通过文化的交流实现信息的交换。每只青蛙都具有自己的文化。每只青蛙的文化被定义为问题的一个解。湿地的整个青蛙群体被分为不同的子群体，每个子群体有着自己的文化，执行局部搜索策略。在子群体中的每个个体有着自己的文化，并且影响着其他个体，也受其他个体的影响，并随着子群体的进化而进化。当子群体进化到一定阶段以后，各个子群体之间再进行思想的交流（全局信息交换）实现子群体间的混合运算，一直到所设置的条件满足为止。

数学模型

　　 算法参数　　与其他优化算法一样，SFLA亦具有一些必要的计算参数，包括F：蛙群的数量；m：族群的数量；n：族群中青蛙的数量；Smax：最大允许跳动步长；Px：全局最好解；Pb：局部最好解；Pw：局部最差解；q：子族群中蛙的数量；LS：局部元进化次数以及SF：全局思想交流次数等。　　 更新策略　　对于青蛙群体，具有全局最好适应度的解表示为 U g；对于每一个子族群，具有最好适应度的解表示为 UB，最差适应度的解表示为 UW。首先对每个子族群进行局部搜索，即对子族群中最差适应度的青蛙个体进行更新操作，更新策略为　　青蛙更新距离 Ds=rand()*(Pb-Pw) （1）　　更新后的青蛙 newDw=oldPw+Ds（-Dmax≦Ds≦Dmax） （2）　　其中， Ds 表示青蛙个体的调整矢量， Dmax表示青蛙个体允许改变的最大步长。如设 Uw=[1 3 5 4 2], UB=[2 1 5 3 4],允许改变的最大步长 Dmax =3，若rand=0.5 ，则 U q(1) =1+min{int[0.5 × (2−1)],3}=1; U q(2) =3+max{int[0.5×(1−3)], −3}=2;依此相同的操作完成更新策略后可得到一个新解 U q=[1 2 5 4 3].

过程

　　 全局搜索过程　　步骤l 初始化。确定蛙群的数量、种群以及每个种群的青蛙数。　　步骤2 随机产生初始蛙群，计算各个蛙的适应值。　　步骤3 按适应值大小进行降序排序并记录最好解Px，并且将蛙群分成族群。把F个蛙分配到m个族群Y，Y，Y…,Y中去，每个族群包含n个蛙，从而使得Yk=[X(j),f(j)|X(j)=X(k+m*(j-1), f(j)=f(k+m*(j-1),j=1,…,n,k=1,…,m].这里X（j）表示蛙群中的第j蛙，f(j)表示第j个蛙的目标函数值。　　步骤4根据SFLA算法公式，在每个族群中进行元进化。　　步骤5将各个族群进行混合。在每个族群都进行过一轮元进化之后，将各个族群中的蛙重新进行排序和族群划分并记录全局最好解Px。　　步骤6检验计算停止条件。如果满足了算法收敛条件，则停止算法执行过程，否则转到步骤3。通常而言，如果算法在连续几个全局思想交流以后，最好解没有得到明显改进则停止算法。某些情况下，最大函数评价次数也可以作为算法的停止准则。　　 局部搜索过程　　局部搜索过程是对上述步骤4的进一步展开，具体过程　　如下：　　步骤4—1设im=O，这里im是族群的计数器。用来与族群总数m进行比较。设iN=0，这里iN是局部进化的计数器，用来与Ls进行比较。　　步骤4-2根据式(1)在第l，，1个族群中选择q个蛙进入子族群，确定Pb和Pw并设im=im+1。　　步骤4-3设iN=iN+1。　　步骤4—4根据式(2)和式(3)改进子族群中的最差蛙的位置。　　步骤4—5如果步骤4—4改进了最差蛙的位置(解)，就用新产生的位置取代最差蛙的位置。否则就采用Px代替式(2)中的PB，重新更新最差蛙的位置。　　步骤4—6如果步骤4-5没有改进最差蛙的位置，则随机产生一个处于湿地中任何位置的蛙来替代最差的蛙。　　步骤4—7如果iN<LS，则转到步骤4-3。　　步骤4—8如果im<m，则转到步骤4-2，否则转到全局搜索过程的步骤5。　　 算法停止条件　　SFLA通常采用两种策略来控制算法的执行时间：　　1)在最近的K次全局思想交流过程之后，全局最好解没有得到明显的改进；　　2)算法预先定义的函数评价次数已经达到。　　3)已有标准测试结果。　　无论哪个停止条件得到满足，算法都要被强制退出整个循环搜索过程。

 
 
clc
clear all
close all
 
%--------------------------------------------------------------------------
% 问题: N个工件,M台机器的确定型流水车间调度问题
 
% 工件数N=20,机器数M=10时,有限次数的最优解 fval=14.9263,
% x =  [16   4   18   15   12   11   2   1   6   7   3   5   20 ...
%       10   8   14   13   19   17   9]
 
N = 20                              % 工件数(解矢量长度)
M = 10                              % 机器数
 
rand('state',N+M);                  % 固定时间矩阵
T = rand(M,N);                      % 产生时间矩阵,行数M1为机器数,列数N为工件数
rand('state',sum(100*clock));       % 种子恢复随机
 
%--------------------------------------------------------------------------
% 必需参数
 
popsize = 50;                       % 种群规模
maxgen = 50;                        % 最大进化代数
method = 4                          % 方法选择,1 - 伪并行小生境自适应遗传算法(PPNSA)
                                    %         2 - 混合蛙跳算法+变异算子(SFLA+MO)
                                    %         3 - 批处理蛙跳算法(BFLA),为SFLA的改进算法
                                    %         4 - PPNSA+扰动算子(末选算法,收敛速度中,较易跳出局部极小)
                                    %         5 - SFLA+MO+扰动算子(次选算法,收敛速度快,最易陷入局部极小)
                                    %         6 - BFLA+扰动算子(首选算法,收敛速度中,可能陷入局部极小)
type = 1;                           % 初始化方式,1 - 随机初始化(缺省设置)
                                    %           2 - 启发式初始化
                                    
%--------------------------------------------------------------------------
% 函数调用
 
[X,fval,F] = SFLA(T,popsize,maxgen,method,type);
% 混合蛙跳算法（Shuffled Frog-Leaping Alogrihtm,SFLA）
% 输入参数:
% T - 时间矩阵
% popsize - 种群规模
% maxgen - 最大进化代数
% method - 方法选择,1 - 伪并行小生境自适应遗传算法(PPNSA)
%                  2 - 混合蛙跳算法+变异算子(SFLA+MO)
%                  3 - 批处理蛙跳算法(BFLA),为SFLA的改进算法
%                  4 - PPNSA+扰动算子(末选算法,收敛速度中,较易跳出局部极小)
%                  5 - SFLA+MO+扰动算子(次选算法,收敛速度快,最易陷入局部极小)
%                  6 - BFLA+扰动算子(首选算法,收敛速度中,可能陷入局部极小)
% type - 初始化方式,1 - 随机初始化(缺省设置)
%                  2 - 启发式初始化
% 输出参数:
% X - 最优适应度对应的解
% fval - 最优适应度值
% F - 最优,平均,最差适应度
 
%--------------------------------------------------------------------------
% 结果作图
 
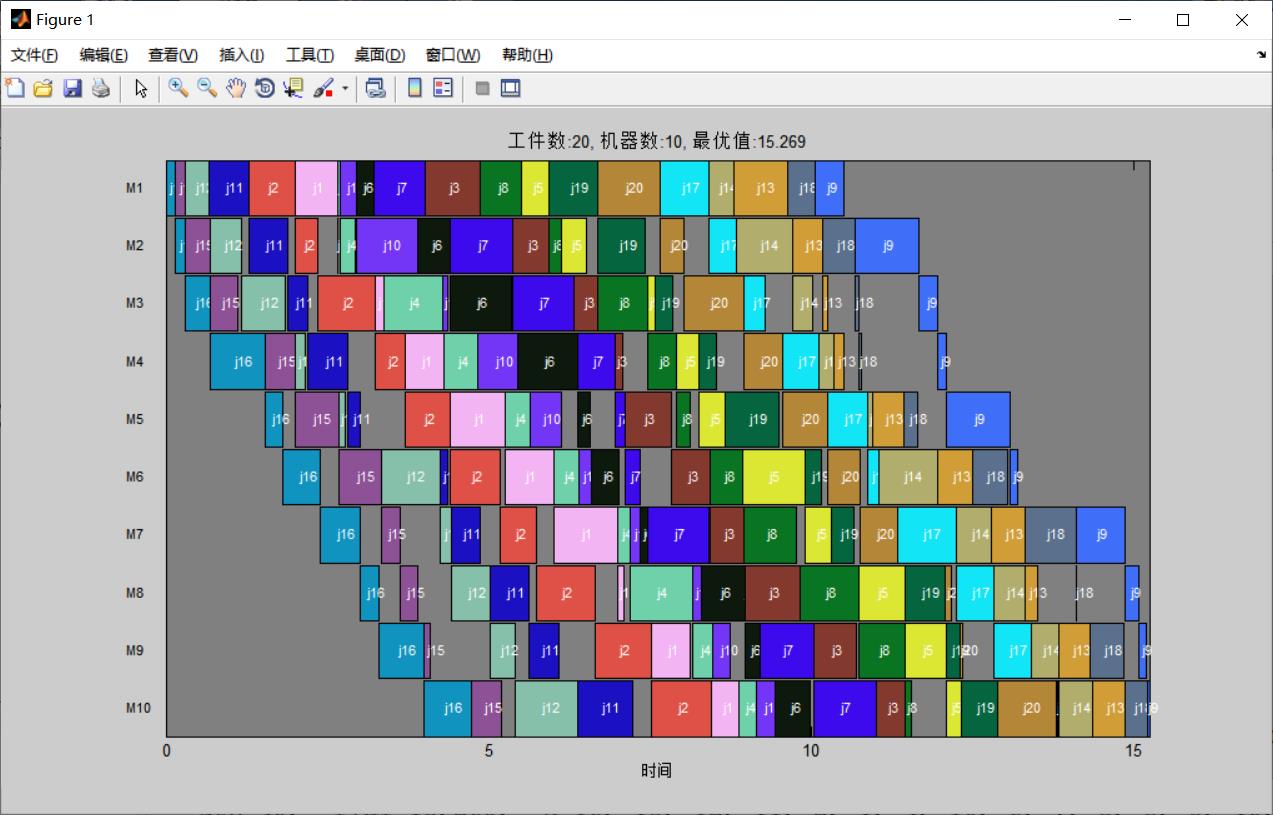
figure(1)
FigSche(X,T);
 
figure(2);
plot(1:maxgen,F,'.-'); grid on;
legend('最优','平均','最差',3);
xlabel('进化代数'); ylabel('适应度');
set(gcf,'position',[700 200 500 400])
set(gca,'XLim',[1 maxgen]);
title(['工件数:',num2str(N),' 机器数:',num2str(M),', 最优值:',num2str(fval)]);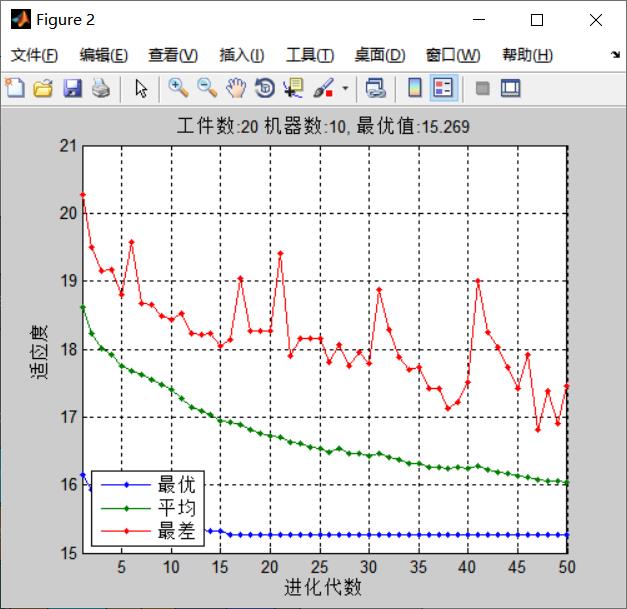

 

完整代码添加QQ1575304183