车间调度基于matlab改进的帝国企鹅算法求解车间调度问题含Matlab源码 2041期

Posted 2022-08-29 海神之光

一、车间调度简介

1 车间调度定义
车间调度是指根据产品制造的合理需求分配加工车间顺序，从而达到合理利用产品制造资源、提高企业经济效益的目的。车间调度问题从数学上可以描述为有n个待加工的零件要在m台机器上加工。问题需要满足的条件包括每个零件的各道工序使用每台机器不多于1次，每个零件都按照一定的顺序进行加工。

2 传统作业车间调度
传统作业车间带调度实例

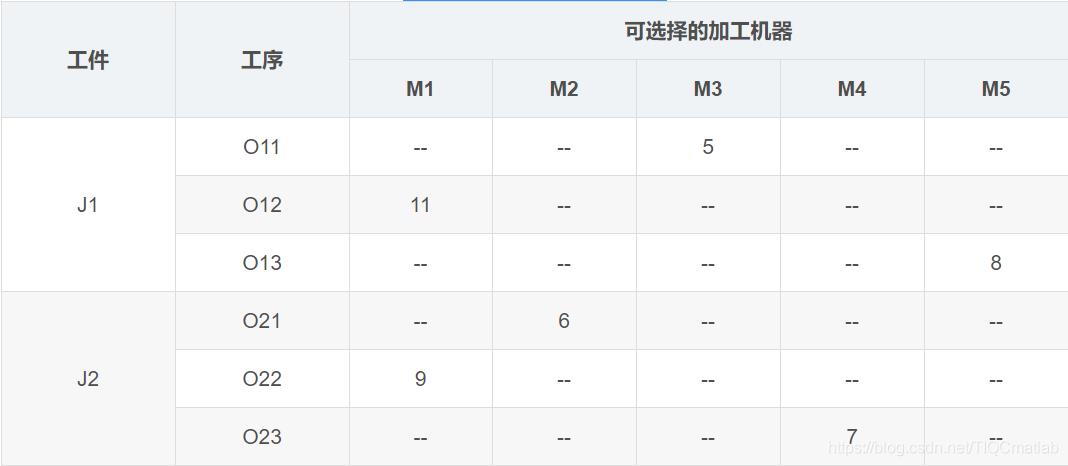
有若干工件，每个工件有若干工序，有多个加工机器，但是每道工序只能在一台机器上加工。对应到上面表格中的实例就是，两个工件，工件J1有三道工序，工序Q11只能在M3上加工，加工时间是5小时。
约束是对于一个工件来说，工序的相对顺序不能变。O11->O12->O13。每时刻，每个工件只能在一台机器上加工；每个机器上只能有一个工件。
调度的任务则是安排出工序的加工顺序，加工顺序确定了，因为每道工序只有一台机器可用，加工的机器也就确定了。
调度的目的是总的完工时间最短（也可以是其他目标）。举个例子，比如确定了O21->O22->O11->O23->O12->O13的加工顺序之后，我们就可以根据加工机器的约束，计算出总的加工时间。
M2加工O21消耗6小时，工件J2当前加工时间6小时。
M1加工O22消耗9小时，工件J2当前加工时间6+9=15小时。
M3加工O11消耗5小时，工件J1当前加工时间5小时。
M4加工O23消耗7小时，工件J2加工时间15+7=22小时。
M1加工O12消耗11小时，但是要等M1加工完O22之后才开始加工O12，所以工件J1的当前加工时间为max(5,9)+11=20小时。
M5加工O13消耗8小时，工件J2加工时间20+8=28小时。
总的完工时间就是max(22,28)=28小时。

2 柔性作业车间调度
柔性作业车间带调度实例（参考自高亮老师论文
《改进遗传算法求解柔性作业车间调度问题》——机械工程学报）

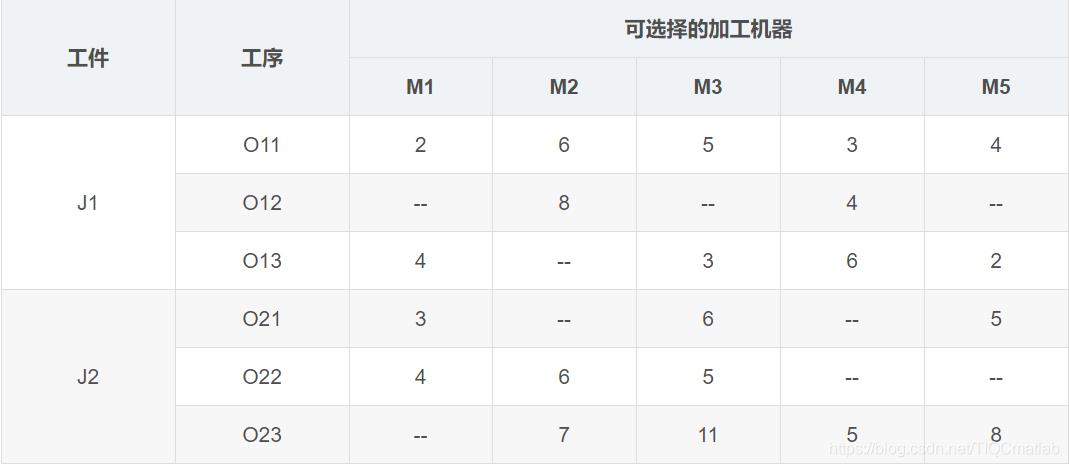
相比于传统作业车间调度，柔性作业车间调度放宽了对加工机器的约束，更符合现实生产情况，每个工序可选加工机器变成了多个，可以由多个加工机器中的一个加工。比如上表中的实例，J1的O12工序可以选择M2和M4加工，加工时间分别是8小时和4小时，但是并不一定选择M4加工，最后得出来的总的完工时间就更短，所以，需要调度算法求解优化。

相比于传统作业车间，柔性车间作业调度的调度任务不仅要确定工序的加工顺序，而且需要确定每道工序的机器分配。比如，确定了O21->O22->O11->O23->O12->O13的加工顺序，我们并不能相应工序的加工机器，所以还应该确定对应的[M1、M3、M5]->[M1、M2、M3]->[M1、M2、M3、M4、M5]->[M2、M3、M4、M5]->[M2、M4]->[M1、M3、M4、M5]的机器组合。调度的目的还是总的完工时间最短（也可以是其他目标，比如机器最大负荷最短、总的机器负荷最短）

二、帝企鹅算法简介

目前，关于帝企鹅算法在国内外研究较少，在中对该算法进行了分析，并且与常见的粒子群算法、萤火虫算法进行了对比分析. 帝企鹅从事各种活动，如狩猎、群体觅食，是群居性动物.每当恶劣的气候来临，它们会挤在一起防风御寒.帝企鹅在南极极端冬季期间主要以集群的方式互相取暖来度过−40 ℃ 的冬季. 为了保证每只企鹅都能取暖，因此每只企鹅都在平等地做出贡献，同时它们的社交行为极为团结以及分工明确. 集群的行为可归纳如下.
1 确定集群边界范围　
设定在帝企鹅蜷缩取暖的过程中所选择的位置范围在多边形的网格范围内，帝企鹅在聚集的过程中至少与两只以上的帝企鹅相邻，邻居的选择是随机的；而在帝企鹅集群过程中范围的边界是不规则的多边形，因此用围绕住帝企鹅集群的风的梯度来表示整体集群的边界，在此定义风速 和其梯度 、 ，集群边界 ，可表示为
γ = ∆α, (8) µ = α+iβ. (9) W

2 计算集群层次周围的温度　
南极严酷的外界环境使得帝企鹅在迁徙过程中面对寒冷天气会采取集群取暖来保持温度. 若当前聚集半径 d>0.5 时，其温度 W=0；当 d<0.5 时，其温度 W=1. 温度梯度曲线可以描述为

其中， 为最大迭代次数，x 为当前迭代次数，温度的表达式

3 计算帝企鹅间的距离　
在集群范围内帝企鹅间的距离表示为该个体与集群中心帝企鹅的距离，集群距离公式如下：

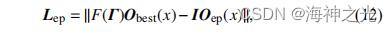
其中， 代表帝企鹅距中心距离； x 表示当前迭代数； 和 用于帝企鹅体积设置的影响向量因子，
避免个体间的冲突； 为 x 轮最优解；表示当前帝企鹅的位置向量； 定义帝企鹅的主体社会地位，负责区别最优个体与普通个体. 向量和 计算如下：

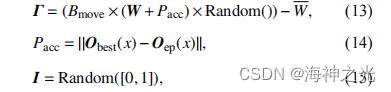
其中 ， 是移动步长参数，这里 的值设置为 2.5， 通过比较与最优的差异来定义多边形网格精度，而 是一个随机函数. 函数计算如下：

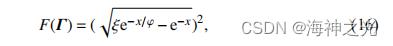
其中，ξ 和 φ是控制参数，其值分别在（2,3）（1.5,2）的范围内能得出更好的结果.

4 帝企鹅位置更新　帝企鹅集群中的个体通过向集群中心帝企鹅 Q 的方向移动更新位置信息，其位置更新如下：
Oep(x+1) = Obest(x)−ΓLep, (17)
其中，Oep(x+1)代表皇帝企鹅的下一个更新位置.在迭代过程中，一旦移动者重新定位，帝企鹅的上述参数将被重新计算.

三、部分源代码

%% 数量固定
% TSP issues with different starting points and a fixed number of travellers
%% 这是使用原始算法的直接求解结果，添加专用于本问题的更新方式可以进一步提高精度
% This is the direct result of using the original algorithm,
% adding some specific update methods to this problem can further improve the accuracy
clc;
clear;
close all;
warning off

%% 固定随机数种子
noRNG=1;
rng(‘default’)
rng(noRNG)

%% 载入数据
data.numPJM=[3,5,7,9,11;
5,10,20,70,90;
3,5,7,15,19];
data.boundT=[5,10];
noPro=[1:length(data.numPJM(1,:))];
%parpool(8)
option.repeatNum=24;
%%
j=1;
%% 随机生成数据
data.Process=[];
data.numJ=data.numPJM(2,j);
data.numM=data.numPJM(1,j);
data.numP0=data.numPJM(3,j);
for noJ=1:data.numJ
for noP=1:data.numP0
data.Process=[data.Process;noJ,noP,rand(1,data.numM)(data.boundT(2)-data.boundT(1))+data.boundT(1)];
end
end
%%
data.numP=length(data.Process(:,1));
dim=data.numPdata.numM;
%%
option.dim=dim;
lb=0;
ub=1;
option.lb=lb;
option.ub=ub;
if length(option.lb)==1
option.lb=ones(1,option.dim)*option.lb;
option.ub=ones(1,option.dim)*option.ub;
end

%option.fobj0=option.fobj;
option.showIter=0;
%% 算法参数设置 Parameters
% 基本参数
option.numAgent=100; %种群个体数

% 帝企鹅算法
option.v_lb=-(option.ub-option.lb)/4;
option.v_ub=(option.ub-option.lb)/4;
option.w2=0.5; %weight of Moving strategy III
option.w4=1;%weight of Moving strategy III
option.w5=1;%weight of Moving strategy III
option.pe=0.01; % rate to judge Premature convergence

option.gapMin=5; % min gap
option.dec=2; % dec of gap
option.L=10; % Catastrophe
%%
option.p1_GA=0.9;
option.p2_GA=0.1;
%% DE
option.F=0.5;
option.CR=0.5;
%% Imroved AFO
option.P_stratage=[0.05,0.2,0.7];
option.p=0.1;
option.alpha=10;
option.gama=1;
str_legend=[‘IAFO’];
selectedAlgorithm=[@IAFO_Final1];
option.maxIteration=data.numJ1000/option.numAgent; %最大迭代次数
option.maxEfs=data.numJ1000;
option.dim=dim;
option.gap0=ceil(sqrt(option.maxIteration*2))+1;
lb=-ones(1,dim)*0;
ub=ones(1,dim)1;
option.lb=lb;
option.ub=ub;
%%
%% 初始化种群个体
%% 使用算法求解
for ii=1:length(selectedAlgorithm)
option.fobj=@aimFcn_FJSP;
x=ones(option.numAgent,option.dim);
y=ones(option.numAgent,1);
for i=1:option.numAgent
x(i,:)=rand(size(option.lb)).(option.ub-option.lb)+option.lb;
y(i)=option.fobj(x(i,:),option,data);
end
rng(noRNG)
tic
[bestY(ii,:),bestX(ii,:),recordingii]=selectedAlgorithmii(x,y,option,data);
recordingT(ii,j)=toc;
end
%%
figure
hold on
plot(recording1.bestFit_EFs(1:option.maxEfs),‘LineWidth’,2)
legend(str_legend)
set(gca,‘LooseInset’,get(gca,‘TightInset’))
%%
rng(1)
option.color=rand(50,3)*0.5+0.5;
for ii=1:length(selectedAlgorithm)
option.fobj=@aimFcn_FJSP;
str=str_legendii;
[fit(ii),result(ii)]=option.fobj(bestX(ii,:),option,data);
drawPc_FJSP(result(ii),option,data,str)
end

四、运行结果

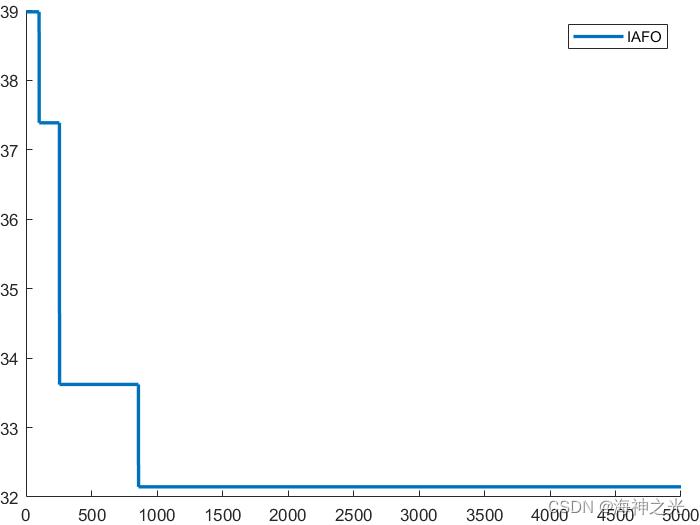
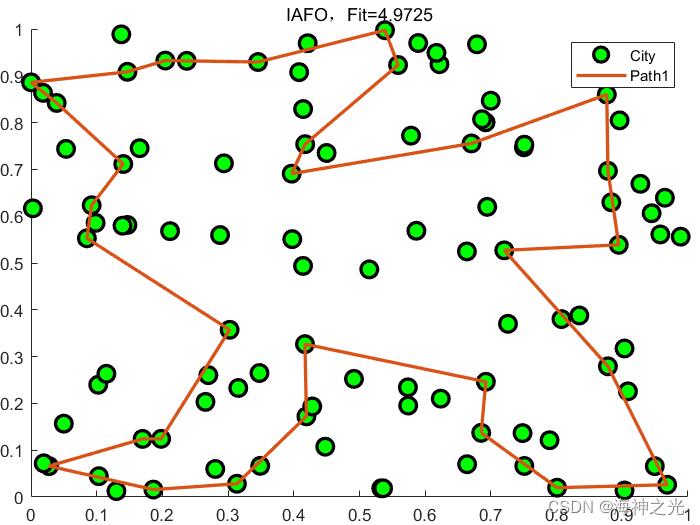
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周萧,王万良,徐新黎.解决作业车间调度问题的混合差分进化算法[J].轻工机械. 2010,28(05)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除