VRP问题基于模拟退火遗传实现带时间窗的车辆路径规划问题

Posted 2021-06-05 博主QQ2449341593

　模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。根据Metropolis准则，粒子在温度T时趋于平衡的概率为e-ΔE/(kT)，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

Return Top

模拟退火算法的模型 　　

模拟退火算法可以分解为解空间、目标函数和初始解三部分。 　

 

模拟退火的基本思想: 　　

(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)， 每个T值的迭代次数L 　　

(2) 对k=1，……，L做第(3)至第6步： 　　

(3) 产生新解S′ 　　

(4) 计算增量Δt′=C(S′)-C(S)，其中C(S)为评价函数 　　

(5) 若Δt′<0则接受S′作为新的当前解，否则以概率exp(-Δt′/T)接受S′作为新的当前解. 　　

(6) 如果满足终止条件则输出当前解作为最优解，结束程序。 终止条件通常取为连续若干个新解都没有被接受时终止算法。 　　

(7) T逐渐减少，且T->0，然后转第2步。

模拟退火的算法流程图如下:

 

 

模拟退火算法新解的产生和接受可分为如下四个步骤： 　　

第一步是由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。 　　

第二步是计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生，所以目标函数差的计算最好按增量计算。事实表明，对大多数应用而言，这是计算目标函数差的最快方法。 　　

第三步是判断新解是否被接受,判断的依据是一个接受准则，最常用的接受准则是Metropo1is准则: 若Δt′<0则接受S′作为新的当前解S，否则以概率exp(-Δt′/T)接受S′作为新的当前解S。 　　

第四步是当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。此时，当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。 　　模拟退火算法与初始值无关，算法求得的解与初始解状态S(是算法迭代的起点)无关；模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法；模拟退火算法具有并行性

如果你对退火的物理意义还是晕晕的，没关系我们还有更为简单的理解方式。想象一下如果我们现在有下面这样一个函数，现在想求函数的（全局）最优解。如果采用Greedy策略，那么从A点开始试探，如果函数值继续减少，那么试探过程就会继续。而当到达点B时，显然我们的探求过程就结束了（因为无论朝哪个方向努力，结果只会越来越大）。最终我们只能找打一个局部最后解B。

 

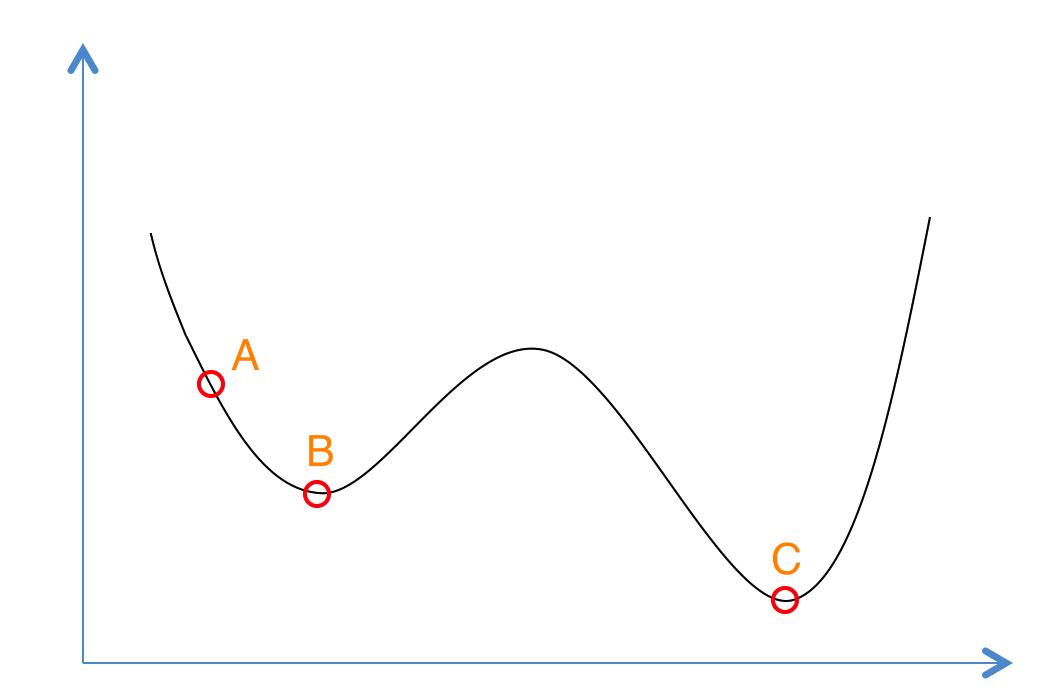
模拟退火其实也是一种Greedy算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以上图为例，模拟退火算法在搜索到局部最优解B后，会以一定的概率接受向右继续移动。也许经过几次这样的不是局部最优的移动后会到达B 和C之间的峰点，于是就跳出了局部最小值B。

根据Metropolis准则，粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为

 

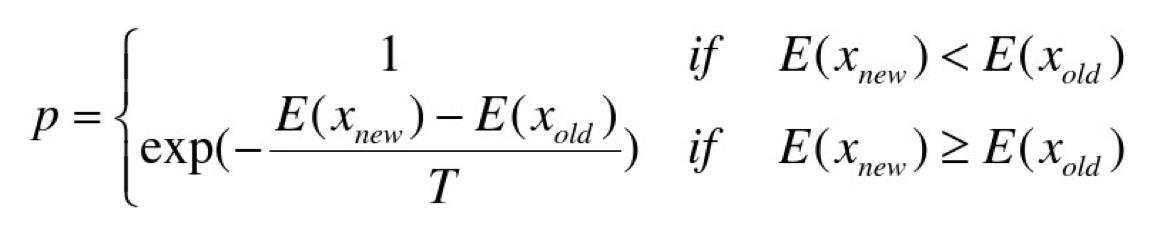
Metropolis准则表明，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：P(dE) = exp( dE/(kT) )。其中k是一个常数，exp表示自然指数，且dE<0。所以P和T正相关。这条公式就表示：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（因为退火的过程是温度逐渐下降的过程），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低，P(dE)会逐渐降低。 我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。也就是说，在用固体退火模拟组合优化问题，将内能E模拟为目标函数值 f，温度T演化成控制参数 t，即得到解组合优化问题的模拟退火演算法：由初始解 i 和控制参数初值 t 开始，对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代，并逐步衰减 t 值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。

总结起来就是：

• 若f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解)，则总是接受该移动；

• 若f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）相当于上图中，从B移向BC之间的小波峰时，每次右移（即接受一个更糟糕值）的概率在逐渐降低。如果这个坡特别长，那么很有可能最终我们并不会翻过这个坡。如果它不太长，这很有可能会翻过它，这取决于衰减 t 值的设定。

关于普通Greedy算法与模拟退火，有一个有趣的比喻：

• • 普通Greedy算法：兔子朝着比现在低的地方跳去。它找到了不远处的最低的山谷。但是这座山谷不一定最低的。这就是普通Greedy算法，它不能保证局部最优值就是全局最优值。

  • 模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向低处，也可能踏入平地。但是，它渐渐清醒了并朝最低的方向跳去。这就是模拟退火。

带时间窗的VRP问题描述：

假设在一个供求关系系统中，车辆从货源取货，配送到对应的若干配送点。车辆存在最大载货量，且配送可能有时间限制。需要合理安排取货时间，组织适当的行车路线，使用户需求得到满足，同时使某个代价函数最小，比如总工作时间最少、路径最短等。可以看出TSP问题是VRP问题的一种简单特殊形式。因此，VRP也是一种NP hard 问题。

目前解决此种问题的办法有多种，主要以启发式算法为主。包括退火算法、遗传算法、蚁群算法、禁忌算法等。

下面建立带时间窗的VRP模型：

 

 

 

 

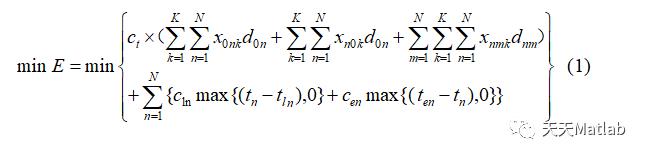
clc;
clear all
close all
t0=cputime;%计时开始
filename='.\\Solomon\\c101.txt';
[NO,XCOORD, YCOORD,DEMAND,READY_TIME,DUE_DATE,SERVICE_TIME]=textread(filename,'%s%s%s%s%s%s%s','headerlines',8);
%初始化
timewindows=[str2num(char(READY_TIME))';str2num(char(DUE_DATE))'];
coordinate=[str2num(char(XCOORD)),str2num(char(YCOORD))];
demand=str2num(char(DEMAND))';
service=str2num(char(SERVICE_TIME))';
D=distanse(coordinate);
popsize=80;%种群数量
capacity = 200;%车子载重
%经验公式m=[Σgi /aq]＋1,粗求车辆数
a = 0.8;   %【3】
k1 = round((sum(abs(demand))./(a*capacity)))-2;    %最小车辆数
k2 = round((sum(abs(demand))./(a*capacity)))+1;    %最大车辆数
% k1=size(NO);
% k2=k1+10;
original = 100;%初始每辆车的载货量
C=500;%C为停止代数，遗传到第 C代时程序停止,C的具体取值视问题的规模和耗费的时间而定
Pc=0.9;%交叉概率
Pm=0.4;%变异概率
%  R = zeros(1,n+k);
% tempR = zeros(1,n+k);
minvalue = 1000000;%随便设置的最优值，不能太小
for k = k1:1:k2 %每种车辆数做一次寻优
         [tempR,tempvalue] = Run_VRP(D,demand,popsize,timewindows,k,capacity,original,C,Pc,Pm,service);%运算返回最优路径R和其总距离Rlength
    if min(tempvalue) < minvalue
        minvalue = min(tempvalue);%如果小于最小适应度值，替代&& min(tempvalue)>100
               R = tempR;%保存最小路径
        minvehicle = k;%保存最小车辆数量
            shiyingdu=tempvalue ;%保存最小染色体
    end
   
end
disp(['最优染色体',num2str(R)]);
disp(['最小车辆数',num2str(minvehicle)]);
disp(['最小里程数',num2str(minvalue)]); 
figure(1)
sz=100;
% scatter(coordinate(:,1),coordinate(:,2),50);%客户位置
hold on
[n,nn] = size(D);%节点个数
for i=2:n
    plot(coordinate(i,1),coordinate(i,2),'ro','MarkerSize',5,'MarkerEdgeColor','k','MarkerFaceColor','b');
   text(coordinate(i,1)-0.001,coordinate(i,2)+0.005,[num2str(i-1)],'Fontsize',10);hold on
end
hold on
plot(coordinate(1,1),coordinate(1,2),'p','MarkerSize',30,'MarkerEdgeColor','k','MarkerFaceColor','y');hold on%发货中心
ss=0;
cost=zeros(k,1);
for j=1:length(R)-1
    if R(j)==0
        ss=ss+1;
    end
    switch ss
        case 1
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)]);hold on%%画出车辆1的路程
         
        case 2
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','r');hold on%%画出车辆2的路程
        
        case 3
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','g');hold on %%画出车辆3的路程
          
        case 4
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','k');hold on %%画出车辆3的路程
         
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','y');hold on %%画出车辆3的路程
           
        case 6
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','m');hold on %%画出车辆3的路程
        
        case 7
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[1 0.6 0.3]);hold on %%画出车辆3的路程
         
        case 8
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.5 0.5 0.5]);hold on %%画出车辆3的路程
           
        case 9
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.6 0.4 0.7]);hold on %%画出车辆3的路程
          
        case 10
             line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.8 0.4 0.7]);hold on %%画出车辆3的路程
       
        case 11
             line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.6 0.6 0.7]);hold on %%画出车辆3的路程
           
        case 12
             line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.6 0.4 0.7]);hold on %%画出车辆3的路程
               otherwise
            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','c');hold on %%画出车辆4的路程
          
    end
end
minvalue1=sum(cost);
title(['车辆数',num2str(minvehicle)]);
xlabel('横坐标');
ylabel('纵坐标')
figure(2)
plot(1:C-1,shiyingdu,'b-');
xlabel('迭代次数');
ylabel('适应度');

 
 
 
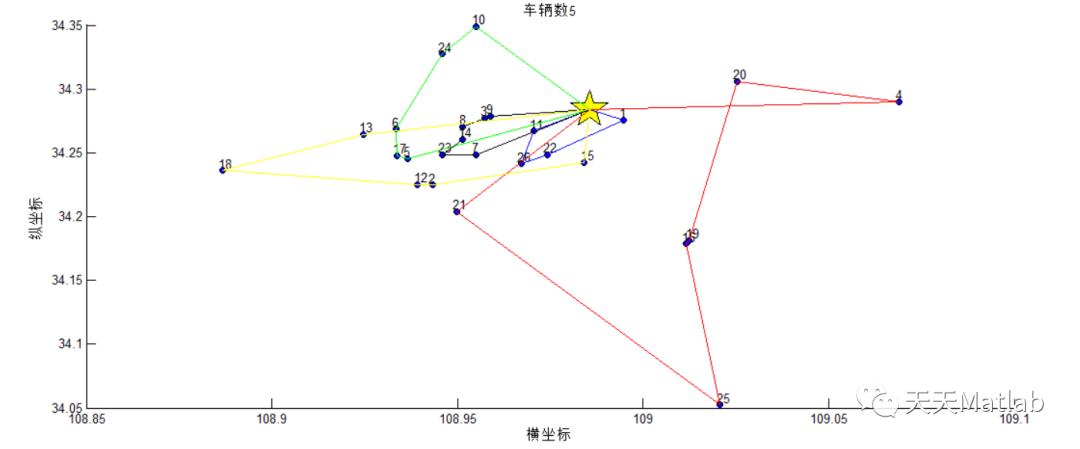
最优染色体0   1  22  26  11   0  21  25  16  19  20   4   0   5  17   6  24  10   0   9   3   8  14  23   7   0  13  18  12   2  15   0
最小车辆数5
最小里程数377.3607
完整代码添加QQ1575304183