leetcode 39. 组合总和---回溯篇2

Posted 2021-06-04 大忽悠爱忽悠

组合总和题解集合

• 回溯法
• 总结

---

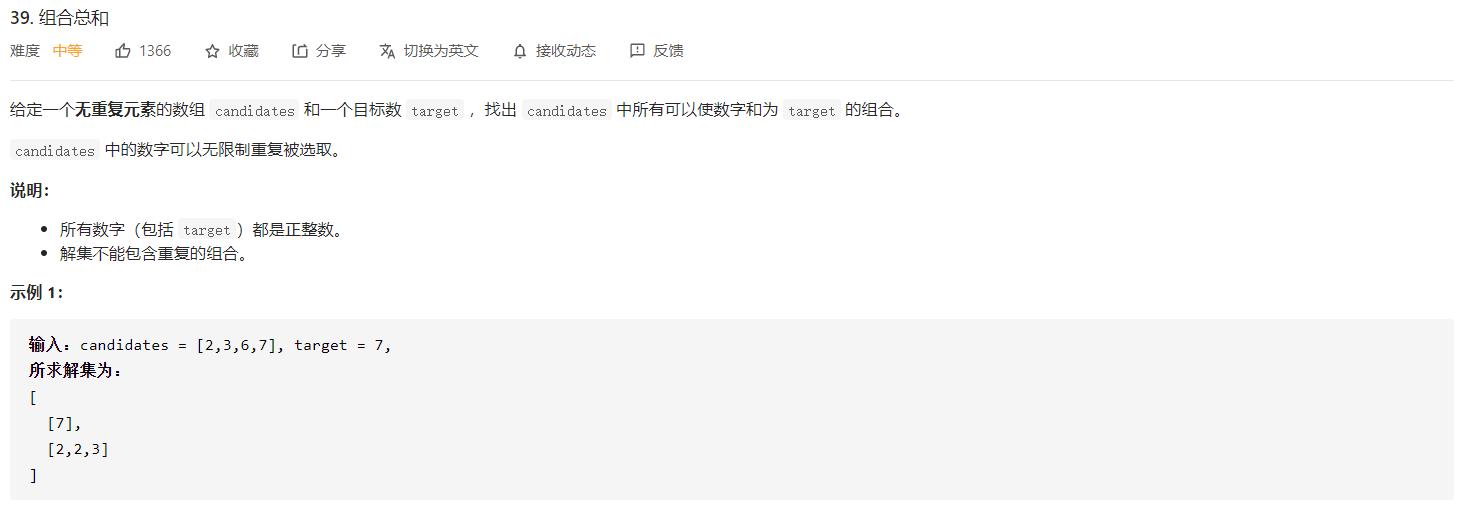
回溯法

这里还是把问题转化为多叉树的遍历问题，但是这里需要提前对数组进行排序，用来去除重复结果，如果不懂排序如何去重的建议先看leetcode 40. 组合总和 II—回溯篇3
三数之和

为什么会有重复结果，可以参考下图:

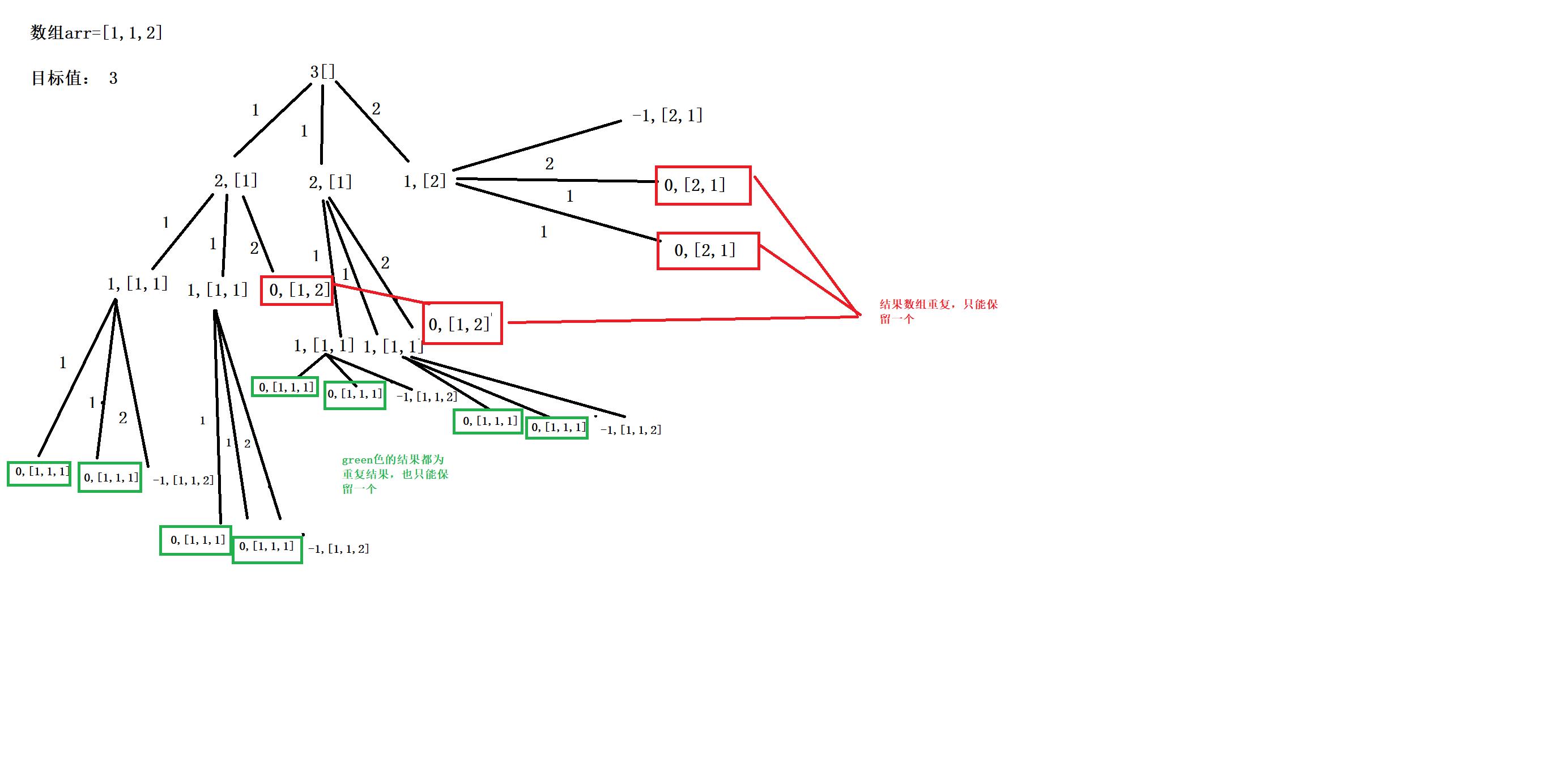
重复源头1：

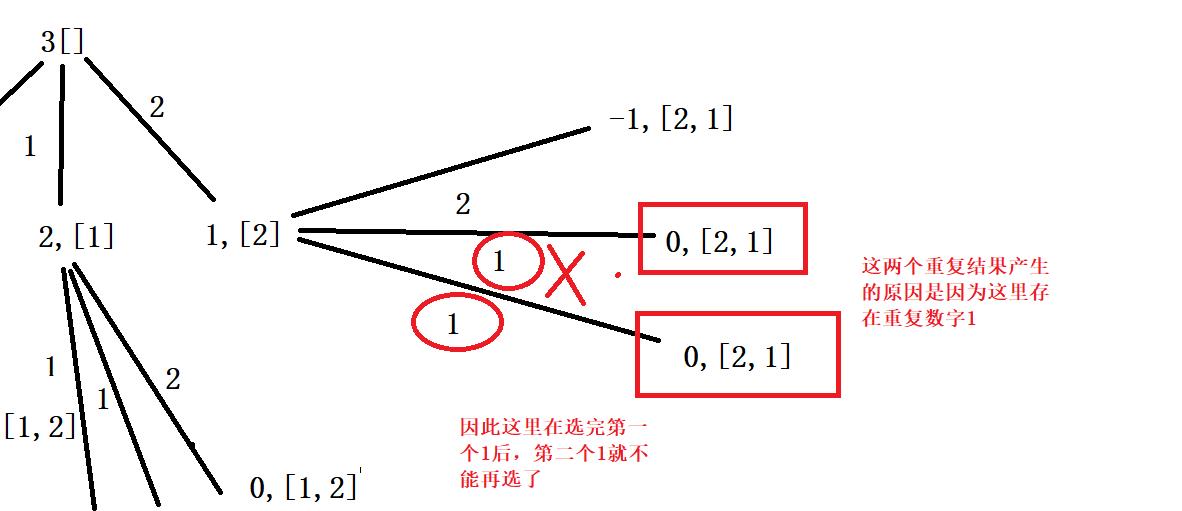
针对上诉情况的代码:if(i>start&&arr[i]==arr[i-1]) continue;

但这里题目中说了，没有重复数字，因此不需要写上面的代码，如果下次出现了重复数字，就需要考虑写上上面的代码。

重复源头2:

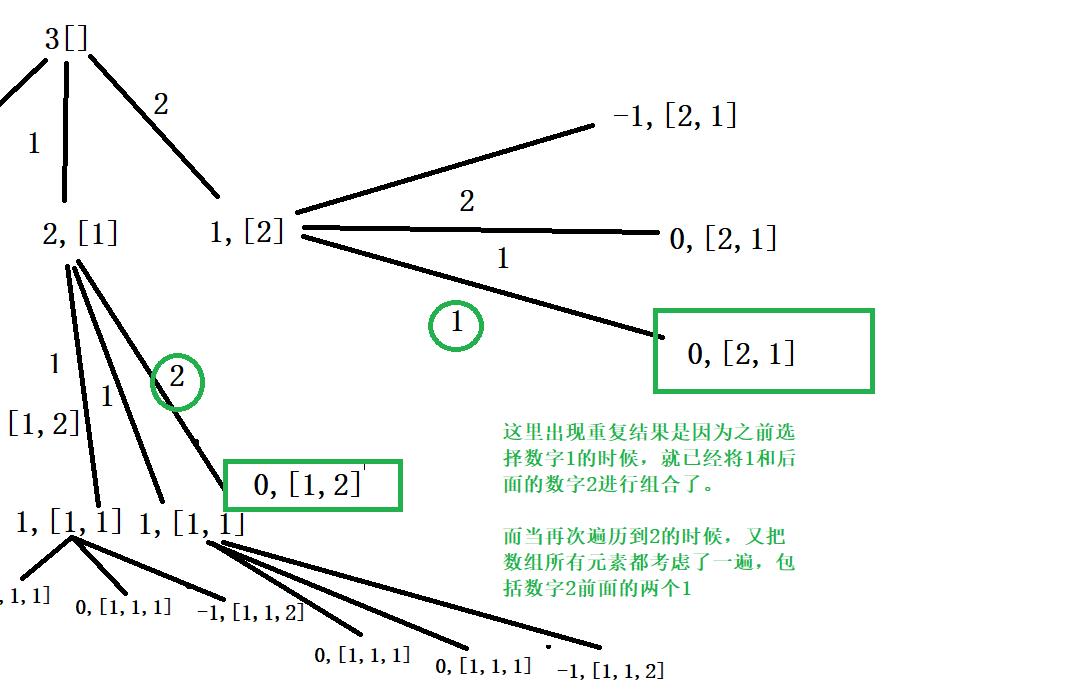
虽然这里每个数字可以重复选择，但这里在选择数字1的时候，会把数组后面包括前面的数字都选择一遍，也包括数字2.

但是轮到2的时候，也会把数组所有元素过一遍，挨个进行组合试探，因此又和前面的1进行了一遍组合，相当于进行了两次重复的组合

解决方法:

在进行当前元素选择时，只考虑与当前元素下标大的包括自身在内的元素进行匹配组合，防止重复组合。

一句话:当前元素只考虑与下标大于等于自己的元素进行匹配（数组要事先排好序）

代码:

class Solution {
	vector<vector<int>> ret;
public:
	vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
	{
		vector<int> num;
		dfs(candidates, target, num, 0);
		return ret;
	}
	void dfs(vector<int>& candidates, int target,vector<int>& num,int index)
	{
		if (target == 0)
		{
			ret.push_back(num);
			return;
		}
		if (target < 0) return;
		for (int i = index; i < candidates.size(); i++)
		{
			num.push_back(candidates[i]);
			dfs(candidates, target - candidates[i], num, i);
			num.pop_back();
		}
	}
};

注意与leetcode 40. 组合总和 II—回溯篇3的区别，这里不能这样写:

	for (int i = index; i < candidates.size()&&target-candidates[i]>=0; i++)

原因:这里我们没有对数组进行排序，因此可能后面会出现更小的数字，满足条件，如果想像上面那么写，可以先对数组进行排序

class Solution {
	vector<vector<int>> ret;
public:
	vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
	{
		vector<int> num;
		sort(candidates.begin(), candidates.end());
		dfs(candidates, target, num, 0);
		return ret;
	}
	void dfs(vector<int>& candidates, int target,vector<int>& num,int index)
	{
		if (target == 0)
		{
			ret.push_back(num);
			return;
		}
		for (int i = index; i < candidates.size()&& target-candidates[i]>=0; i++)
		{
			num.push_back(candidates[i]);
			dfs(candidates, target - candidates[i], num, i);
			num.pop_back();
		}
	}
};

---

总结

如果这里出现了重复数字，那么这里还可以用排序后哈希法去重，但是这里没有重复数字，因此哈希法去重在这里不起作用