216. 组合总和 III-----回溯篇4

Posted 2021-06-04 大忽悠爱忽悠

组合总和 ||| 题解结合

• 回溯法
• 总结

---

回溯法

本篇题解给的不是特别详细，因为本题与leetcode 40. 组合总和 II—回溯篇3相比，就增添了一个限制条件罢了，建议先看第40题再来看本题

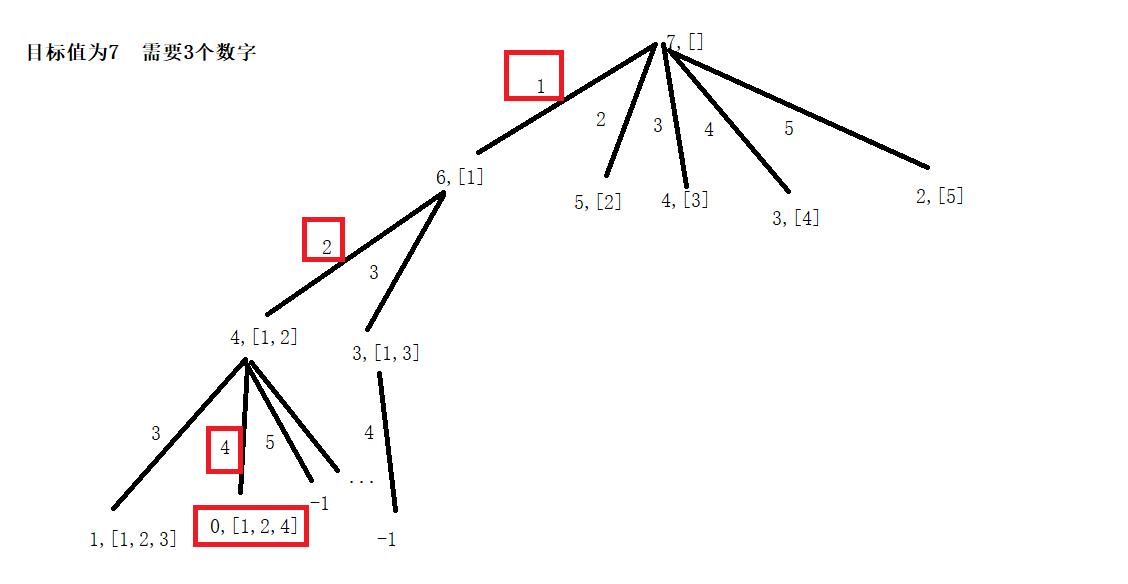
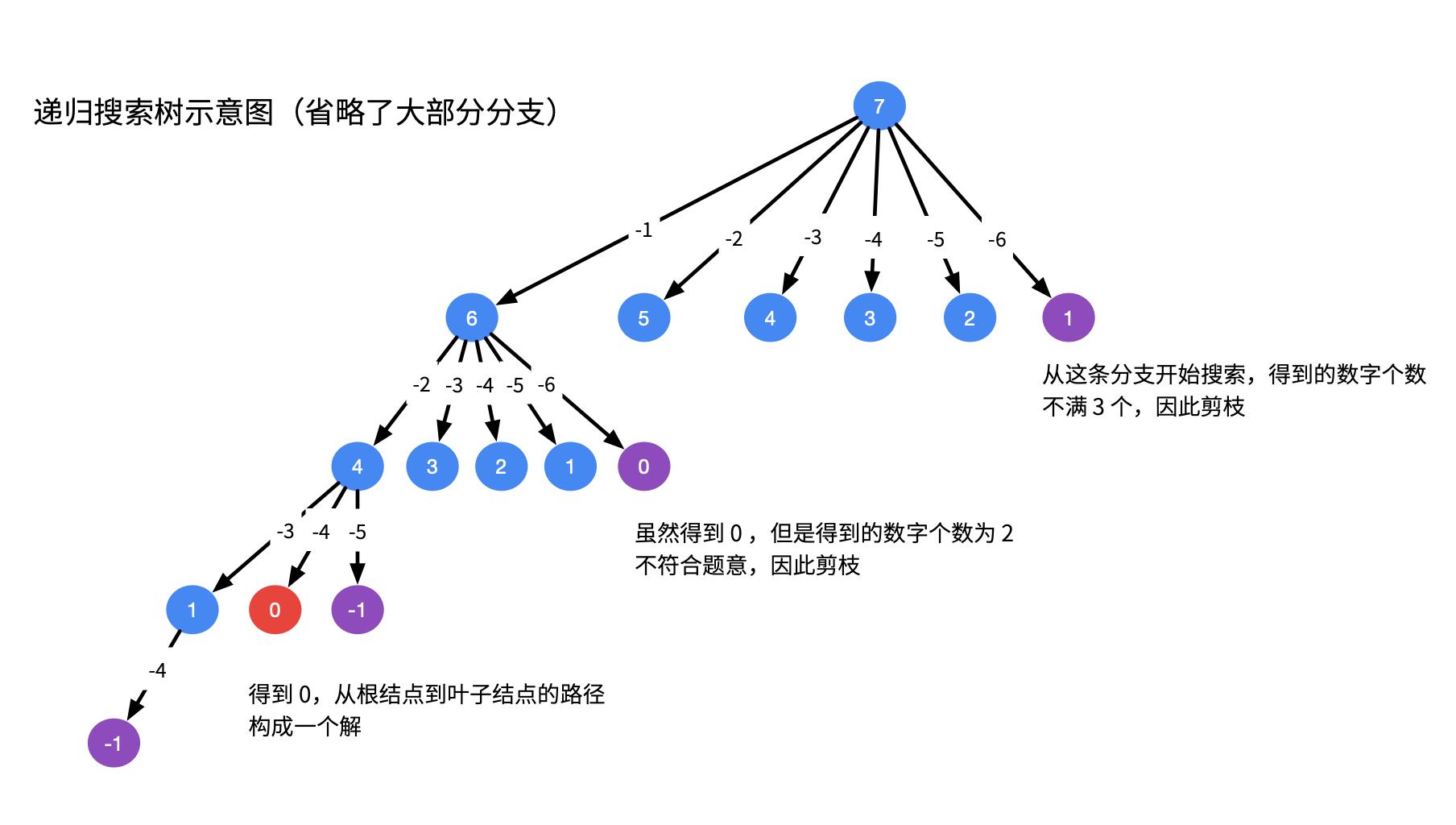
显然这里与leetcode 40. 组合总和 II—回溯篇3较为相似，1—9中每个数字都只能选择一次，且这里结果数组中不能出现重复数字。

注意这里1—9就相当于第40题中给出的数组，并且里面的元素已经排好了序，因此我们下面的限制条件可以这样写:

		for (int i = index; i <= 9&&n-i>=0; i++)

对于排好序的数组来说，如果当前数字都比目标值大，那么后面的数字只会比目标值更大，更加不能选择

这里又额外添加的限制条件是结果数组里面包含的元素个数刚好为n个

因此我们也只需要在递归的结束条件都加上这个判断即可。

代码：

class Solution {
	vector<vector<int>> ret;
public:
	vector<vector<int>> combinationSum3(int k, int n) 
	{
		vector<int> num;
		dfs(k, n, num, 1);
		return ret;
	}
	void dfs(int k,int n,vector<int>& num,int index)
	{
		if (num.size() > k) return;
		if (n == 0 && num.size() == k)
		{
			ret.push_back(num); return;
		}
		for (int i = index; i <= 9&&n-i>=0; i++)
		{
			num.push_back(i);
			dfs(k, n - i, num, i+1);
			num.pop_back();
		}
	}
};

---

总结

「回溯算法」根据当前决策有多少种选择，对应了两套模板。

• 每一次独立的决策只对应 选择 和 不选 两种情况：
• 确定结束回溯过程的 base case
• 遍历每个位置，对每个位置进行决策（做选择 -> 递归 -> 撤销选择）

void dfs(当前位置, 路径(当前结果), 结果集) {
    if (当前位置 == 结束位置) {
        结果集.add(路径);
        return;
    }
        
    选择当前位置;    
    dfs(下一位置, 路径(当前结果), 结果集);
    撤销选择当前位置;
    dfs(下一位置, 路径(当前结果), 结果集);
}

• 每一次独立的决策都对应了多种选择（通常对应了每次决策能选择什么，或者每次决策能选择多少个 …）:
• 确定结束回溯过程的 base case
• 遍历所有的「选择」
• 对选择进行决策 (做选择 -> 递归 -> 撤销选择)

void dfs(选择列表, 路径(当前结果), 结果集) {
    if (满足结束条件) {
        结果集.add(路径);
        return;
    }
        
    for (选择 in 选择列表) {
        做选择;
        dfs(路径’, 选择列表, 结果集);
        撤销选择;
    }
}