论文阅读|《基于制造公差的复杂机械产品精准选配方法》及Python部分实现

Posted 2021-06-02 码丽莲梦露

《基于制造公差的复杂机械产品精准选配方法》

计算机集成制造系统/2020/西安交通大学

这篇文章考虑尺寸误差和形位误差，提出一种基于零部件优先级及质量要求优先级的选配方法，并提出一种选配中行为公差的有效表征形式。

1 基于制造公差信息的选配优化模型

1.1 曲柄连杆机构中形位公差的有效表征

形位公差的作用：

（1）形位公差做尺寸链组成环

（2）形位公差做尺寸链封闭环

下图的曲柄连杆机构包含5挡主轴颈和4挡连杆轴颈。考虑到曲柄连杆机构中，若同一组零件配合间隙差别较大、松紧不一，会造成主轴颈中心不重合，运转时受冲击较大。因此，在选配中除了保证配合间隙满足质量要求外，还需要尽可能减小曲轴的各处主轴颈中心的相对位置度公差，以及同步运动的连杆轴承孔中心的相对位置公差。

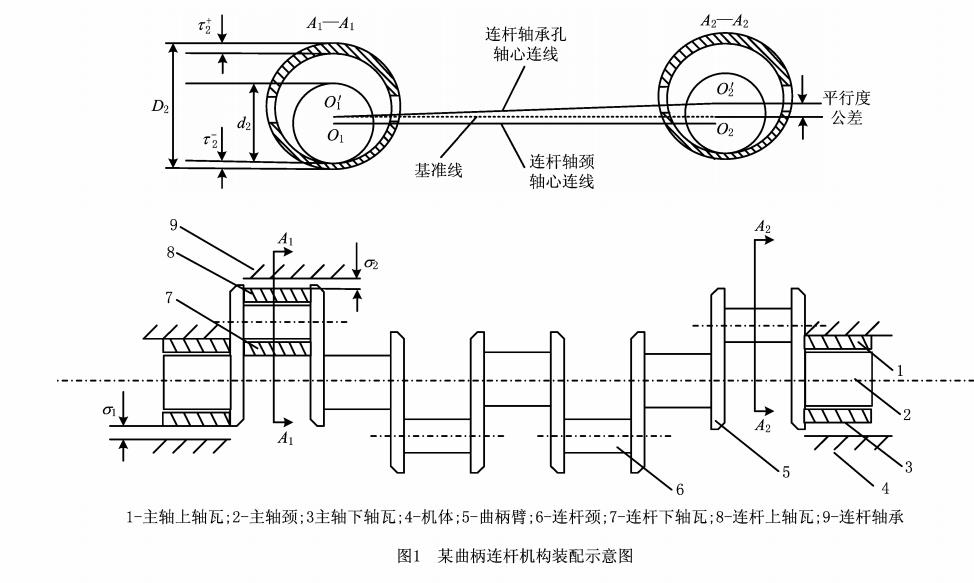
1.1.1主轴颈中心相对位置度公差的计算

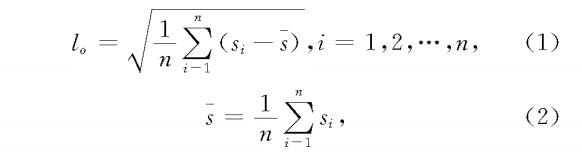
1.1.2 连杆轴颈、连杆轴承孔配合的平行度公差P0的计算

1.2 基于装配精度和装配成功率的选配模型

1.2.1 基于田口质量观的装配精度评价模型

    田口博士以产品的装配质量特性值偏离理想设计值的平均损失为优化的目标函数，保证装配精度的可靠性和稳定性。

             

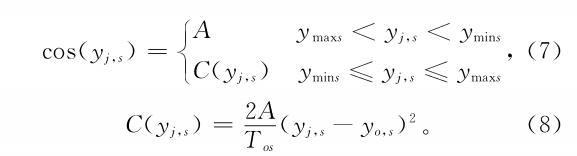
1.2.2 基于装配成功率的装配质量评价模型

     在机械产品装配不完全互换的前提下，即使待装配的零部件全部合格，装配后的产品也会出现不满足质量要求的情况。因此，将装配成功率也作为选配质量的重要评价指标，质量要求FRs的装配成功率为：

装配精度与装配尺寸、尺寸链等相关知识点：装配精度与装配尺寸_crazy_girl_me的博客-CSDN博客

1.3 基于影响度的选配优先级评价模型

    在复杂机械产品的选配中，由于质量要求较多，在使用智能算法优化时往往面临收敛缓慢的问题。考虑到产品最终的质量要求实测值是由组成该产品各个零部件公差项实测值决定的，可将尺寸链中不同组成换对封闭环的影响度作为零部件优先级的评定标准，影响度越大的零件，优先级越高。

1.3.1 选配零部件优先级评价

影响度用来描述装配尺寸链中每一个组成环尺寸公差对封闭环尺寸积累的贡献大小。本文根据装配尺寸链中各组成环的公差波动，结合该组成环对封闭环环的影响度，确定各零部件的选配优先级，

选配优先系统PL:

1.3.2 质量要求优先级评价

在复杂机械产品多质量要求的选配中，各质量要求间应存在主次关系，而传统做法是根据各质量要求对最终产品性能的影响程度来确立其重要程度。

2 基于遗传算法的模型求解‘

2.1 基于零部件单元的基因编码方法

注：交叉变异用的比较普通，解码之后在实现时具体体现，

论文实现

3 Instance

这为从论文中提取的案例数据

import random
import numpy as np

#机械零件设计公差数据
Design_tolerance_data = [
    [[61, 0, 0.018, 0.15]],                         # 机体 D1 主轴承孔孔径
    [[57, -0.018, 0, 0.4],[45, -0.020, 0, 0.4]],    # 曲轴 d1 主轴颈直径 /d2 连杆轴颈直径
    [[48, 0, 0.016, 0.15]],                         # 连杆 D2 连杆轴承孔径
    [[2, -0.015, 0.003, 0.17]],                     # 主轴瓦 厚度 t1
    [[1.5, -0.013, -0.001, 0.13]]                   # 连杆轴瓦 厚度 t2
]

#装配质量要求
#数据分别表示：公差上限 公差下限 封闭环目标值 个数 优先级系数
Assembly_QR=[
    [0.020,0.042,0.031,5,0.58],  #配合间隙1
    [0.018,0.048,0.033,4,0.42],  #配合间隙2
]

#质量特性数据 分别表示：D1 d1 d2 D2 t1 t2
# QCD=[]
# for i in range(10):
#     QCi=[]
#     for i in range(len(Design_tolerance_data)):
#         for j in range(len(Design_tolerance_data[i])):
#             L=Design_tolerance_data[i][j][0]
#             T=random.uniform(Design_tolerance_data[i][j][1],Design_tolerance_data[i][j][2])
#             T=round(T,3)
#             QCi.append(L+T)
#     QCD.append(QCi)
# print(QCD)
QCD=[[61.002, 56.998, 44.981, 48.010, 1.987, 1.497],
     [61.001, 56.999, 44.981, 48.016, 1.990, 1.492],
     [61.013, 56.982, 44.993, 48.011, 1.995, 1.496],
     [61.012, 56.996, 45.000, 48.015, 1.991, 1.492],
     [61.008, 56.984, 44.997, 48.010, 2.001, 1.496],
     [61.015, 56.988, 44.990, 48.015, 1.994, 1.489],
     [61.010, 56.991, 44.989, 48.006, 1.988, 1.496],
     [61.006, 56.995, 44.981, 48.010, 1.992, 1.498],
     [61.012, 56.985, 44.998, 48.014, 1.985, 1.490],
     [61.005, 56.988, 44.986, 48.015, 1.992, 1.494]]

QCD=np.array(QCD)

4 GA

今天只写了编码，之后续上！

from Instance import Design_tolerance_data,Assembly_QR,QCD

class GA:
    def __init__(self,N_Pop=30,O_Pop=30,Pc=0.8,Pm=0.8,Z=300):
        self.N_Pop=N_Pop    #内部种群
        self.O_Pop=O_Pop    #外部种群
        self.Pc=Pc          #交叉概率
        self.Pm=Pm          #变异概率
        self.Z=Z            #迭代次数

    #一条染色体
    def Chromo(self,Num):
        C=[]
        T = []
        for M_num in range(10):
            t = [i for i in range(10)]
            T.append(t)
        for J_num in range(Num):
            for i in range(Num):
                K=random.choice(T[Num])
                C.append(K)
                T[Num].pop(K)
        return C

    def Encode(self):
        P=[]
        for i in range(self.N_Pop+self.O_Pop):
            P.append(self.Chromo(6))
        return P