计算机组成原理——进制间相互转换

Posted 2021-05-29 流楚丶格念

文章目录

• • 各种进制
  • 各种进制的常见书写方式
  • • 二进制优越性
  • 任意进制→十进制
  • • r 进制计数法
    • 举例
  • 二进制↔八进制、十六进制
  • • 二进制 —> 八进制
    • 八进制—> 二进制
    • 二进制 —> 十六进制
    • 二进制 —> 十六进制
  • 十进制→任意进制
  • • 除 x 取余倒排法(x 代表进制数)
    • 十进制→二进制（拼凑法）
  • 真值和机器数

各种进制

进制	举例
二进制： 0,1	二进制： 101.1 —> 1 × 2! + 0 × 2" + 1 × 2# + 1 × 2%" = 5.5
八进制： 0,1,2,3,4,5,6,7	八进制： 5.4 —> 5 × 8# + 4 × 8%" = 5.5
十进制： 0,1,2,3,4,5,6,7,8,9	十进制： 5.5 —> 5 × 10# + 5 × 10%" = 5.5
十六进制： 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F	十六进制： 5.8 —> 5 × 16# + 8 × 16%" = 5.5

各种进制的常见书写方式

二进制优越性

①可使用两个稳定状态的物理器件表示
②0，1 正好对应逻辑值 假、真。方便实现逻辑运算
③可很方便地使用逻辑门电路实现算术运算

任意进制→十进制

采用r 进制计数法每个位数的基数×该进制的位权次幂依次相加就可以啦

r 进制计数法

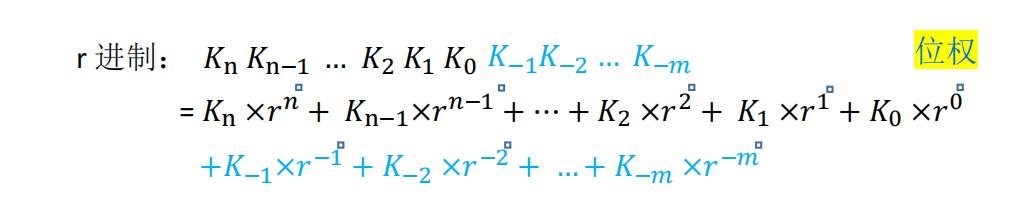
基数：每个数码位所用到的不同符号的个数，r 进制的基数为 r

举例

进制	计算举例
二进制：1 0 0 1 0 0 1 0 . 1 1 0	1 * 2^7 + 1 * 2^4 + 1 * 2^1 + 1 * 2^-1 + 1 * 2^-2 = 146.75
八进制：251.5	2 * 8^2 + 5 * 8^1 + 1 * 8^0 + 5 * 8^-1 = 168.625
十六进制：AE86.1	10 * 16^3 + 14 * 16^2 + 8 * 16^1 + 6 * 16^0 + 1 * 16^-1 = 44678.0625

大家也可以记住常见的二进制各个位的十进制值（右击保存图片收藏）

二进制↔八进制、十六进制

二进制 —> 八进制

3位一组，毎组转换成对应的八进制符号

八进制—> 二进制

每位八进制对应的3位二进制

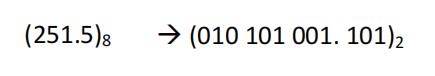
二进制 —> 十六进制

4位一组，毎组转换成对应的十六进制符号

二进制 —> 十六进制

4位一组，毎组转换成对应的十六进制符号

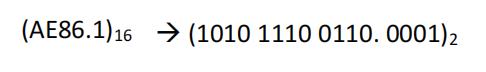
十进制→任意进制

除 x 取余倒排法(x 代表进制数)

完整内容可以参考这个回答：https://zhidao.baidu.com/question/374587905766222524.html

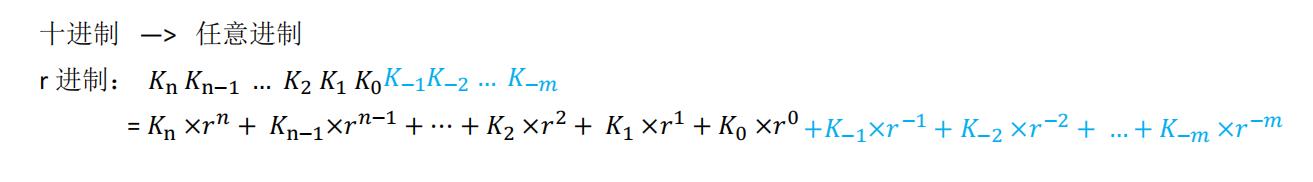
如：75.3 小数部分=0.3

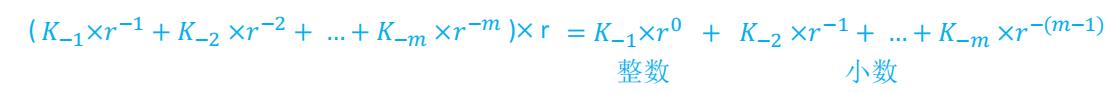
那么我们转化成二进制就是这样

• 整数部分
  - 小数部分
  

十进制→二进制（拼凑法）

用这个图直接凑

真值和机器数

• 真值：符合人类习惯的数字
• 机器数：数字实际存到机器里的形式，正负号需要被“数字化”

例如下面两个数